堆的介绍
堆的结构可以分为大根堆和小根堆,是一个完全二叉树。它的所有元素按完全二叉树的顺序存储方式存储在一个一维数组中,如果满足:Ki <= K2 i+1 且 Ki<= K2 i+2 的(即:每个父节点均不大于其子节点的堆)称为“小根堆”,Ki >= K2 i+1 且 Ki >= K2 i+2称为大根堆。
某个大根堆的顺序存储的样式:
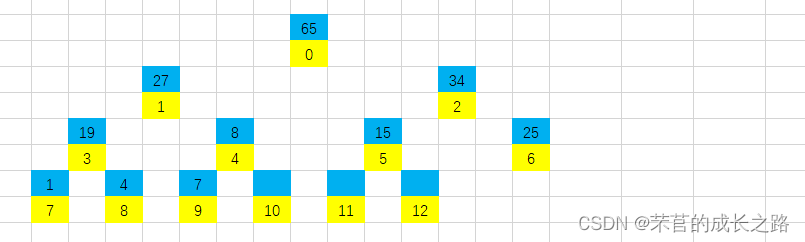
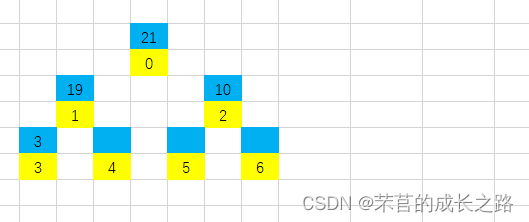
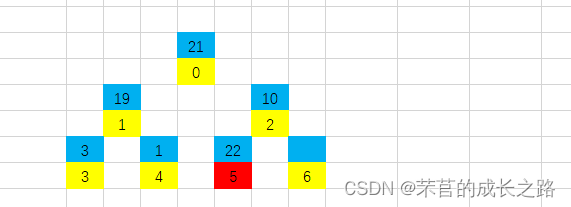
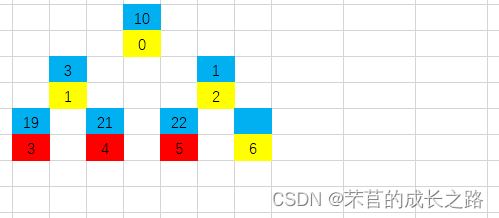
该堆的完全二叉树的样式(黄色为下标,蓝色为元素值):
建堆(以向上调整建大根堆为例)
建堆意味着要根据新插入的数据大小不停地调整父节点和子节点的位置关系,要严格保证父节点均不小于其子节点,但左右孩子节点大小顺序并不做要求!左孩子比右孩子大或者右孩子比左孩子大都是可以的。
其中:
左孩子节点下标 = 父节点下标*2+1;
右孩子节点下标 = 父节点下标*2+2
父亲节点=(孩子节点下标-1)/2。以下以int a[] = {21,19,10 ,3 ,1, 22}为例:
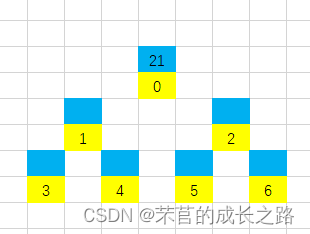
第一步:第0位置放入21;
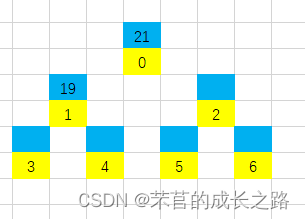
第二步:先对比19和21大小,19小,所以19为21的子节点,所以第1位置插入1:
第三步:先对比10和21大小,10小,所以10放入2号位置:
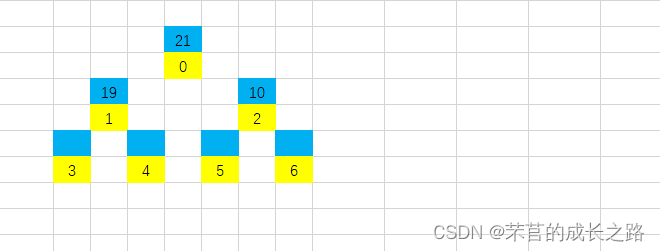
第四步:3比19小,所以3放入3号位;
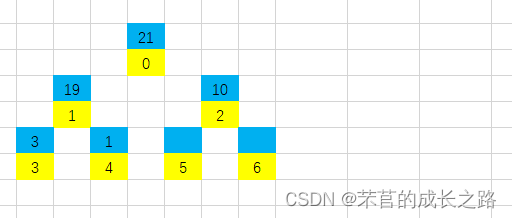
第五步:1比19小,1放入4号位
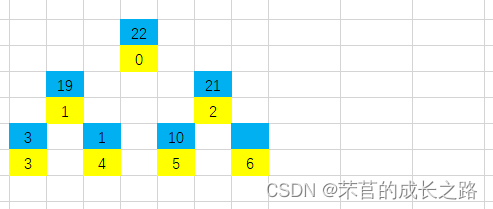
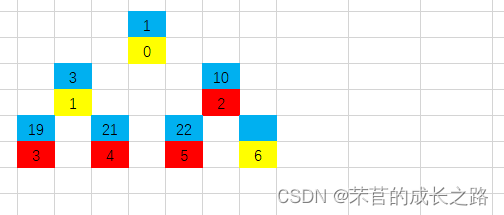
第六步:22比10大,所以10放入5号位,2号位放入22;再对比22和21,22比21大,22放入0号位,21放入2号位。
大根堆构建完成!
构建大根堆核心函数(向上调整方式)
//使用向上调整的方式构建大根堆
void createHeap(int a[],int n){//n是元素下标
if(n==0){//当前就是根节点
return ;
}
int father = (n-1)/2;//建大堆只需要管父节点大于子节点,至于左右节点的大小是不作要求的
while(father>=0){//向上一辈迭代,直到父节点比该节点大并且该节点比其子节点大为止(或者该节点成为根节点)
if(a[n]>a[father]){//如果子节点大于其父节点,交换两者
Swap(&a[n],&a[father]);//交换父子元素
}else{//当前位置符合大根堆要求
return ;//结束
}
//交换父子节点后,向上检查,当前节点变成其父节点,继续对比它和新的父节点大小关系
n = father;//向上一辈
father = (n-1)/2;
}//while
}
排序过程(红色表示排序完成部分,向下调整堆结构)
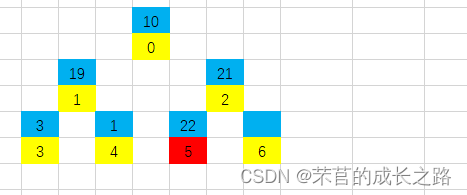
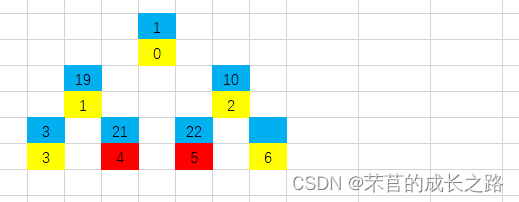
第一步:将堆顶放置堆尾,原堆尾暂放置至堆顶(因为经过调整堆顶肯定是最大值了),此时待排序的堆长度减一(区间从0-5变成0-4了):
第二步:调整现堆顶元素位置。位置0的左右孩子分别为19和21,选择最大的孩子与堆顶元素互换,此时2号位置没有子节点(5号位不在排序区间内了)。
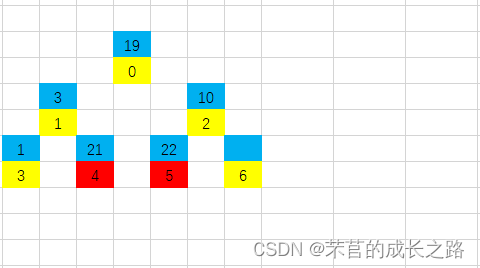
第三步:重复第一步:将1和21互换位置:
第四步:重复第二步:调整现堆顶元素1的位置:1的子节点里19最大,1和19互换:
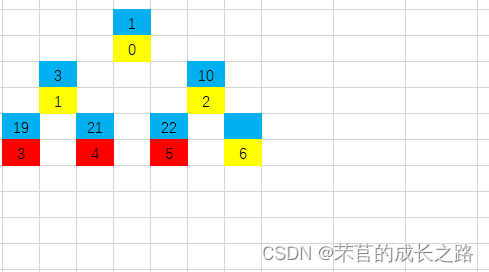
第五步:1的子节点里3比1大,再次进行第二步(4号位置不在排序区间内了,不属于1号位的子节点了):
第六步:重复第一步:19放至堆尾,即和1换位置,1暂成为堆顶:
第七步:重复第二步:1和其最大的子节点10换位置:
第八步:重复第一步:10放至堆尾,1暂成为堆顶:
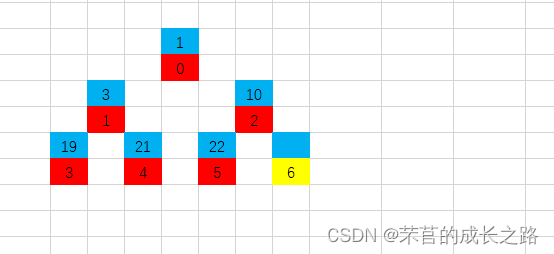
后续步骤就没有调整了,因为元素已经有序了,最后执行结果为:
根据下标,你就会发现,原先的[21 19 10 3 1 22]构建成大根堆就是[22 19 21 3 1 10],排序完成便成了[1 3 10 19 21 22]。这就是堆排序的建堆和调整堆直至其有序的过程。
调整排序代码(向下调整)
//排序过程堆向下调整
void adjustHeap(int a[],int n){//n是待排序的最后一个节点
if(n==0){
return;
}//已经到根节点了
Swap(&a[0],&a[n]);//把堆顶放到最后
n--;//固定一个元素后,整体长度减一
int father = 0;//向下调整以根节点为父节点出发
int maxchild = father*2+1;//左孩子
while(maxchild<=n){
if(maxchild+1<=n&&a[maxchild]<a[maxchild+1]){//两个孩子比较的前提是得有右孩子
maxchild++;//两个孩子找出最大的孩子子节点和父节点比较
}
if(a[maxchild]>a[father]){//如果最大子节点大于其父节点,交换两者
Swap(&a[maxchild],&a[father]);
}
//向下迭代
father = maxchild;//换了左往左下调整换了右就往右下调整
maxchild = father*2+1;
} //while
}
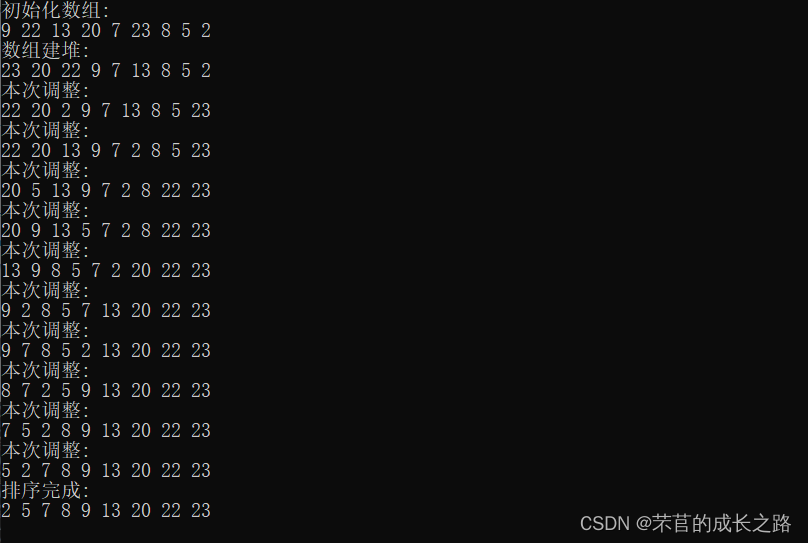
实例1:
实例2:
关于堆排序的时间复杂度
堆排序建堆的时间复杂度为 O(n),选数的时间复杂度为 O(n×log n),即堆排序的时间复杂度为:O(N*logN);
空间复杂度:O(1)。
源代码
/*
广西师范大学 计算机科学与工程学院
GuangXi Normal University
College of Computer Science and Engineering
Student STZ
*/
#include<iostream>
#include<stdio.h>
#include <stdlib.h>
#include <time.h>
using namespace std;
int len=9;//数组长度
#define max 25;
void Swap(int *a,int *b){
int t = *a;
*a = *b;
*b = t;
}
void initial(int a[]){
srand((unsigned)time(NULL));
for(int i=0;i<len;i++){//随机生成10个数
a[i] = rand()%max;
}
}
void showHeap(int a[]){
for(int i=0;i<len;i++){
cout<<a[i]<<" ";
}
cout<<endl;
}
//使用向上调整的方式构建大根堆
void createHeap(int a[],int n){//n是元素下标
if(n==0){//当前就是根节点
return ;
}
int father = (n-1)/2;//建大堆只需要管父节点大于子节点,至于左右节点的大小是不作要求的
while(father>=0){//构建过程
if(a[n]>a[father]){//如果子节点大于其父节点,交换两者
Swap(&a[n],&a[father]);
}else{//当前位置符合大根堆要求
return ;//结束
}
//交换父子节点后,向上检查,当前节点变成其父节点,继续对比它和新的父节点大小关系
n = father;
father = (n-1)/2;
}//while
}
//排序过程堆向下调整
void adjustHeap(int a[],int n){//n是待排序的最后一个节点
if(n==0){
return;
}//已经到根节点了
Swap(&a[0],&a[n]);//把堆顶放到最后
n--;//固定一个元素后,整体长度减一
int father = 0;//向下调整以根节点为父节点出发
int maxchild = father*2+1;//左孩子
while(maxchild<=n){
if(maxchild+1<=n&&a[maxchild]<a[maxchild+1]){//两个孩子比较的前提是得有右孩子
maxchild++;//两个孩子找出最大的孩子子节点和父节点比较
}
if(a[maxchild]>a[father]){//如果最大子节点大于其父节点,交换两者
Swap(&a[maxchild],&a[father]);
}
//向下一辈迭代
father = maxchild;//换了左往左下调整换了右就往右下调整
maxchild = father*2+1;
} //while
}
int main(){
int a[len];
initial(a);
cout<<"初始化数组:\n";
showHeap(a);
for(int i=0;i<len;i++){
createHeap(a,i);
}
cout<<"数组建堆:\n";
showHeap(a);
for(int i=len-1;i>=0;i--){
adjustHeap(a,i);
}
cout<<"排序完成:\n";
showHeap(a);
return 0;
}