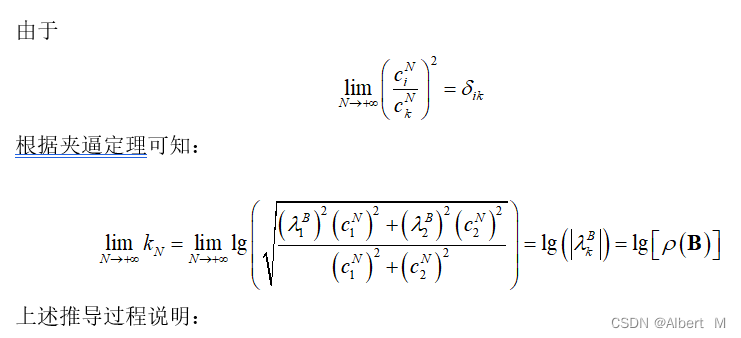1. Richardson 迭代法
求解线性方程组:
A
x
⃗
=
b
⃗
(
∗
)
\bold{A}\vec{x}=\vec{b} \quad(*)
Ax=b(∗)
其中,
A
\bold A
A 若为
n
n
n 阶对称矩阵则要求正定,采用迭代格式:
x
⃗
i
+
1
=
x
⃗
i
+
α
(
b
⃗
−
A
x
⃗
i
)
(
i
=
0
,
1
,
…
;
α
=
c
o
n
s
t
a
n
t
>
0
)
\vec{x}_{i+1}=\vec{x}_i+\alpha(\vec{b}-\bold{A}\vec{x}_i)\quad(i=0,1,\dots;\alpha=constant>0)
xi+1=xi+α(b−Axi)(i=0,1,…;α=constant>0)
进行求解的方法称作Richardson 迭代法。
若
A
\bold A
A 为对称正定矩阵
(
S
P
D
)
(SPD)
(SPD),此时求解线性方程组
(
∗
)
(*)
(∗) 与寻找如下多元二次函数
g
(
x
⃗
)
g(\vec{x})
g(x) 的最小值点的问题等价:
g
(
x
⃗
)
=
1
2
x
⃗
T
A
x
⃗
−
b
⃗
T
x
⃗
g(\vec{x})=\frac{1}{2}\vec{x}^T\bold{A}\vec{x}-\vec{b}^T\vec{x}
g(x)=21xTAx−bTx
说明如下:
一方面,由
u
⃗
\vec{u}
u 处取得二次函数最小值的必要条件:
▽
g
(
u
⃗
)
=
A
u
⃗
−
b
⃗
=
0
⟹
A
u
⃗
=
b
⃗
\bigtriangledown g(\vec{u})=\bold{A}\vec{u}-\vec{b}=0\Longrightarrow\bold{A}\vec{u}=\vec{b}
▽g(u)=Au−b=0⟹Au=b
另一方面,若
A
u
⃗
=
b
⃗
⟹
▽
g
(
u
⃗
)
=
A
u
⃗
−
b
⃗
=
0
\bold{A}\vec{u}=\vec{b}\Longrightarrow\bigtriangledown g(\vec{u})=\bold{A}\vec{u}-\vec{b}=0
Au=b⟹▽g(u)=Au−b=0
且
H
(
g
)
=
A
(
H
e
s
s
i
a
n
矩阵
)
H(g)=\bold{A}\ (Hessian 矩阵)
H(g)=A (Hessian矩阵)
在
x
⃗
=
u
⃗
\vec{x}=\vec{u}
x=u 处正定。故
g
(
x
⃗
)
g(\vec{x})
g(x) 在
u
⃗
\vec{u}
u 处取得极小值,又由于系数矩阵正定,故使得梯度为零的点存在且唯一,故
u
⃗
\vec{u}
u 为最小值点。
采用最速下降法求解该最小值问题:
x
⃗
i
+
1
=
x
⃗
i
−
α
▽
g
(
x
⃗
i
)
=
x
⃗
i
+
α
(
b
⃗
−
A
x
⃗
i
)
\vec{x}_{i+1}=\vec{x}_i-\alpha\bigtriangledown g(\vec{x}_i)=\vec{x}_i+\alpha(\vec{b}-\bold{A}\vec{x}_i)
xi+1=xi−α▽g(xi)=xi+α(b−Axi)
其中,
α
>
0
\alpha>0
α>0反映沿负梯度方向前进的长度。上式实际上就是Richardson 迭代法所采用的迭代格式,说明了Richardson 迭代法的合理性,解释了为何要求
α
>
0
\alpha>0
α>0。
2. Richardson 迭代法的收敛条件
Richardson 迭代格式为:
x
⃗
i
+
1
=
x
⃗
i
+
α
(
b
⃗
−
A
x
⃗
i
)
=
(
E
−
α
A
)
x
⃗
i
+
α
b
⃗
(
i
=
0
,
1
,
…
)
(
1
)
\vec{x}_{i+1}=\vec{x}_i+\alpha(\vec{b}-\bold A\vec{x}_i)=(\bold E-\alpha\bold A)\vec{x}_i+\alpha\vec{b}\quad(i=0,1,\dots)\quad(1)
xi+1=xi+α(b−Axi)=(E−αA)xi+αb(i=0,1,…)(1)
考虑该迭代格式的收敛性,等价于考虑迭代过程中误差的收敛性。设方程组有精确解
x
⃗
\vec{x}
x,则
x
⃗
=
(
E
−
α
A
)
x
⃗
+
α
b
⃗
(
2
)
\vec{x}=(\bold E-\alpha\bold A)\vec{x}+\alpha\vec{b}\quad(2)
x=(E−αA)x+αb(2)
由
(
1
)
−
(
2
)
(1)-(2)
(1)−(2) 得:
e
⃗
i
+
1
=
(
E
−
α
A
)
e
⃗
i
(
i
=
0
,
1
,
…
)
\vec{e}_{i+1}=(\bold E-\alpha\bold A)\vec{e}_i\quad(i=0,1,\dots)
ei+1=(E−αA)ei(i=0,1,…)
则有:
e
⃗
i
=
(
E
−
α
A
)
e
⃗
i
−
1
=
(
E
−
α
A
)
i
e
⃗
0
\vec{e}_i=(\bold E-\alpha\bold A)\vec{e}_{i-1}=(\bold E-\alpha\bold A)^i\vec{e}_0
ei=(E−αA)ei−1=(E−αA)ie0
假设
A
\bold A
A 为实对称矩阵,则
B
≜
E
−
α
A
\bold B\triangleq\bold E-\alpha\bold A
B≜E−αA 为实对称矩阵,其特征值
λ
i
B
(
i
=
1
,
2
,
…
,
n
)
\lambda_i^B\ (i=1,2,\dots,n)
λiB (i=1,2,…,n) 为实数,特征向量
u
⃗
i
(
i
=
1
,
2
,
…
,
n
)
\vec{u}_i\ (i=1,2,\dots,n)
ui (i=1,2,…,n) 两两正交,将误差在
B
\bold B
B 特征向量构成的基上展开,有:
e
⃗
i
=
∑
j
=
1
n
c
j
i
u
⃗
j
=
(
E
−
α
A
)
i
e
⃗
0
=
(
E
−
α
A
)
i
∑
j
=
i
n
c
j
0
u
⃗
j
=
∑
j
=
1
n
c
j
0
(
λ
j
B
)
i
u
⃗
j
⟹
c
j
i
=
c
j
0
(
λ
j
B
)
i
(
j
=
1
,
2
,
…
,
n
)
\vec{e}_i=\sum_{j=1}^nc_j^i\vec{u}_j=(\bold E-\alpha\bold A)^i\vec{e}_0=(\bold E-\alpha\bold A)^i\sum_{j=i}^nc_j^0\vec{u}_j=\sum_{j=1}^nc_j^0(\lambda_j^B)^i\vec{u}_j\\\ \\ \Longrightarrow c^i_j=c_j^0(\lambda_j^B)^i\quad(j=1,2,\dots,n)
ei=j=1∑ncjiuj=(E−αA)ie0=(E−αA)ij=i∑ncj0uj=j=1∑ncj0(λjB)iuj ⟹cji=cj0(λjB)i(j=1,2,…,n)
显然,想要随着迭代过程的进行,误差逐渐收敛,应有
−
1
<
λ
j
B
<
1
(
i
=
1
,
2
,
…
,
n
)
-1<\lambda_j^B<1\quad(i=1,2,\dots,n)
−1<λjB<1(i=1,2,…,n)
即,
ρ
(
E
−
α
A
)
<
1
⟹
{
1
−
α
λ
m
i
n
A
<
1
⟹
λ
m
i
n
A
>
0
1
−
α
λ
m
a
x
A
>
−
1
⟹
0
<
α
<
2
λ
m
a
x
A
\rho(\bold E-\alpha\bold A)<1\Longrightarrow \begin{cases} 1-\alpha\lambda_{min}^A<1\Longrightarrow \lambda_{min}^A>0 \\\\ 1-\alpha\lambda_{max}^A>-1\Longrightarrow0<\alpha<\dfrac{2}{\lambda_{max}^A} \end{cases}
ρ(E−αA)<1⟹⎩
⎨
⎧1−αλminA<1⟹λminA>01−αλmaxA>−1⟹0<α<λmaxA2
上式给出了Richardson 迭代的收敛条件:
ρ
(
E
−
α
A
)
<
1
\rho(\bold E-\alpha\bold A)<1
ρ(E−αA)<1,或者具体来说
(1) 系数矩阵 A \bold A A 对称正定;
(2) α ∈ ( 0 , 2 λ m a x A ) \alpha\in(0,\dfrac{2}{\lambda_{max}^A}) α∈(0,λmaxA2);
此外,上述讨论还说明
ρ
(
E
−
α
A
)
\rho(\bold E-\alpha\bold A)
ρ(E−αA) 越小,误差收敛越快,而
B
\bold B
B 的收敛半径与参数
α
\alpha
α 的选取有关,这意味着存在最佳的
α
\alpha
α 使得Richardson 迭代的收敛速度最快,又:
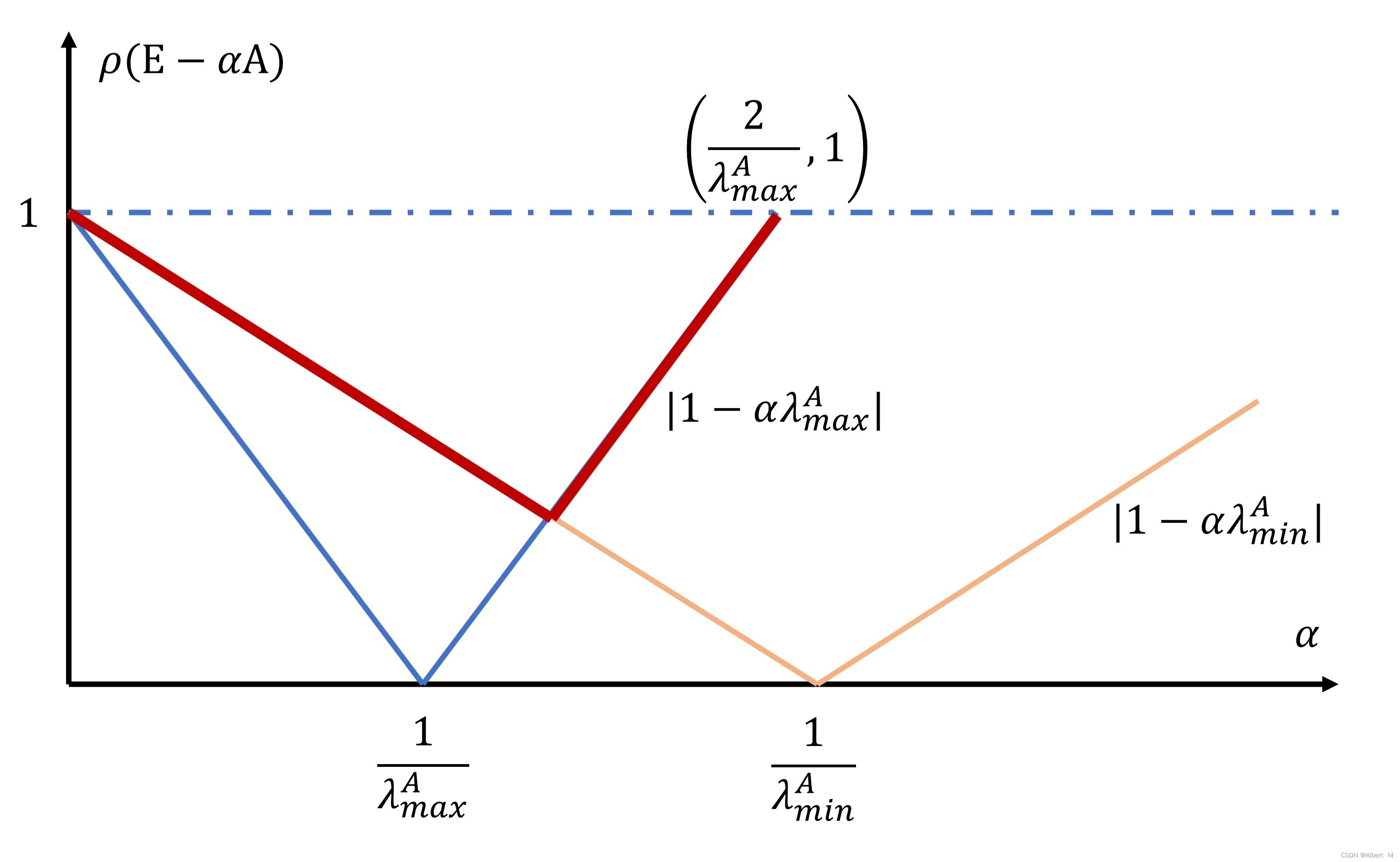
ρ
(
E
−
α
A
)
=
m
a
x
{
∣
1
−
α
m
i
n
A
∣
,
∣
1
−
α
m
a
x
A
∣
}
\rho(\bold E-\alpha\bold A)=max\{|1-\alpha_{min}^A|,|1-\alpha_{max}^A|\}
ρ(E−αA)=max{∣1−αminA∣,∣1−αmaxA∣}
由图可知:
m
i
n
(
ρ
(
E
−
α
A
)
)
=
λ
m
a
x
A
−
λ
m
i
n
A
λ
m
a
x
A
+
λ
m
i
n
A
min(\rho(\bold E-\alpha\bold A))=\dfrac{\lambda^A_{max}-\lambda^A_{min}}{\lambda^A_{max}+\lambda^A_{min}}
min(ρ(E−αA))=λmaxA+λminAλmaxA−λminA
且此时,
α
o
p
t
=
2
λ
m
a
x
A
+
λ
m
i
n
A
\alpha_{opt}=\dfrac{2}{\lambda^A_{max}+\lambda^A_{min}}
αopt=λmaxA+λminA2
3. 算法实现与算例验证
function [x] = Richardson(A,b,x0,alpha,N)
% 函数功能:利用 Richardson 迭代法求解 n 元线性方程组 Ax=b
% 变量说明:
% (1) A = [n,n] - 线性方程组的系数矩阵;
% (2) b = [n,1] - 线性方程组的常数项;
% (3) x = [n,1] - 线性方程组的解;
% (4) alpha - Richardson 迭代法中的参数(>0);
% = "数值" - 按设定的值进行计算(不满足方法条件时,警告);
% = "best" - 按迭代速度最佳的alpha值进行计算;
% (5) n - 线性方程组未知量的个数;
% (6) x0 - 解的初始猜测值;
% (7) N - 迭代次数;
% 检验输入参数是否符合 Richardson 迭代法求解的要求:
if isnumeric(N)
if N <= 0
error("错误:迭代步数[N]应为正整数")
end
if rem(N,1) ~= 0
error("错误:迭代步数[N]应为正整数")
end
else
error("错误:迭代步数[N]应为正整数")
end
n = size(A,1);
if n ~= size(A,2)
error("错误:系数矩阵[A]应为方阵")
end
if size(b,2) ~= 1
error("错误:常数项[b]应为列向量")
end
if n ~= size(b,1)
error("错误:系数矩阵[A]与常数项[b]维度不匹配")
end
if size(x0,2) ~= 1
error("错误:初值[x0]应为列向量")
end
if n ~= size(x0,1)
error("错误:初值[x0]维度不匹配")
end
% 检验线性方程组的系数矩阵是否为对称矩阵,若对称则必须正定:
flag = 0;
for i = 2:n
for j = 1:i-1
if A(i,j) ~= A(j,i)
flag = 1;
end
end
end
if flag == 1
for i = 1:n
if det(A(1:i,1:i)) <= 0
error("错误:系数矩阵[A]对称时应正定")
end
end
end
% 检验输入指定数值参数 alpha 时是否满足要求:
if isnumeric(alpha)
if alpha > 2/vrho(A)
warning("警告:参数[alpha]设置不满足Richardson 迭代法的收敛条件")
end
elseif isstring(alpha)
if strcmp(alpha,"best")
alpha = 2/(max(eig(A))+min(eig(A)));
else
error("错误:参数[alpha]只能为数值或关键字[best]")
end
else
error("错误:参数[alpha]只能为数值或关键字[best]")
end
% Richardson 迭代:
i = 0;
while i < N
x = x0+alpha*(b-A*x0);
i = i+1;
x0 = x;
end
end
利用编写完成的 Richardson 函数求解如下线性方程组
A
x
⃗
=
b
⃗
\bold A\vec{x}=\vec{b}
Ax=b :
[
6
3
3
4
]
[
x
1
x
2
]
=
[
−
3
−
9
]
\begin{bmatrix} 6 & 3 \\ 3 & 4 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} =\begin{bmatrix} -3 \\ -9 \end{bmatrix}
[6334][x1x2]=[−3−9]
该线性方程组的精确解为:
x
⃗
e
x
=
[
1
−
3
]
T
\vec{x}_{ex}=[1\ -3]^T
xex=[1 −3]T
系数矩阵的特征值为:
λ
⃗
A
=
[
1.8377
8.1623
]
T
\vec{\lambda}^{A}=\begin{bmatrix}1.8377&8.1623\end{bmatrix}^T
λA=[1.83778.1623]T
由前面的讨论可知:
使得Richardson迭代法收敛的参数
α
\alpha
α 的取值范围为:
0
<
α
<
2
λ
m
a
x
A
=
0.245
0<\alpha<\frac{2}{\lambda^A_{max}}=0.245
0<α<λmaxA2=0.245
且有:
α
o
p
t
=
2
λ
m
a
x
A
+
λ
m
i
n
A
=
0.2
ρ
o
p
t
=
λ
m
a
x
A
−
λ
m
i
n
A
λ
m
a
x
A
+
λ
m
i
n
A
=
0.6325
\alpha_{opt}=\frac{2}{\lambda^A_{max}+\lambda^A_{min}}=0.2 \\\ \\ \rho_{opt}=\frac{\lambda^A_{max}-\lambda^A_{min}}{\lambda^A_{max}+\lambda^A_{min}}=0.6325
αopt=λmaxA+λminA2=0.2 ρopt=λmaxA+λminAλmaxA−λminA=0.6325
下面实际操作来进行下测试:
- 初值: x ⃗ 0 = [ 0.0 0.0 ] T \vec{x}_{0}=[0.0\quad 0.0]^T x0=[0.00.0]T;
- α = [ 0.06 0.1 0.2 0.22 0.24 0.4 ] T \alpha=\begin{bmatrix}0.06&0.1&0.2&0.22&0.24&0.4\end{bmatrix}^T α=[0.060.10.20.220.240.4]T;
% 程序功能:
% Richardson 函数的测试算例
clear;clc;close all;
% 方程的系数矩阵与常数项:
A = [6,3;3,4];
b = [-3;-9];
% 该方程的精确解:
x_exc = [1;-3];
% 前50步的收敛曲线:
figure(1)
step = 50;
e = zeros(length(alpha),step);
for i = 1:length(alpha)
for j = 0:step
if j == 0
e(i,j+1) = norm(x0-x_exc);
else
[x] = Richardson(A,b,x0,alpha(i),j);
e(i,j+1) = norm(x-x_exc);
end
end
end
semilogy( 1:51,e(1,:), ...
1:51,e(2,:), ...
1:51,e(3,:), ...
1:51,e(4,:), ...
1:51,e(5,:), ...
1:51,e(6,:),'LineWidth',1.8);
legend('\alpha = 0.06','\alpha = 0.10', ...
'\alpha = 0.20','\alpha = 0.22', ...
'\alpha = 0.24','\alpha = 0.40', ...
'Location','northwest', ...
'FontName','Times New Roman', ...
'FontSize',12, ...
'NumColumns',2)
legend('boxoff')
xlabel('Steps \it{N}','FontSize',12,'FontName','Times New Roman')
ylabel('$||\vec{x}-\vec{x}_{ex}||_2$','FontSize',12, ...
'FontName','Times New Roman','Interpreter','latex')
grid on
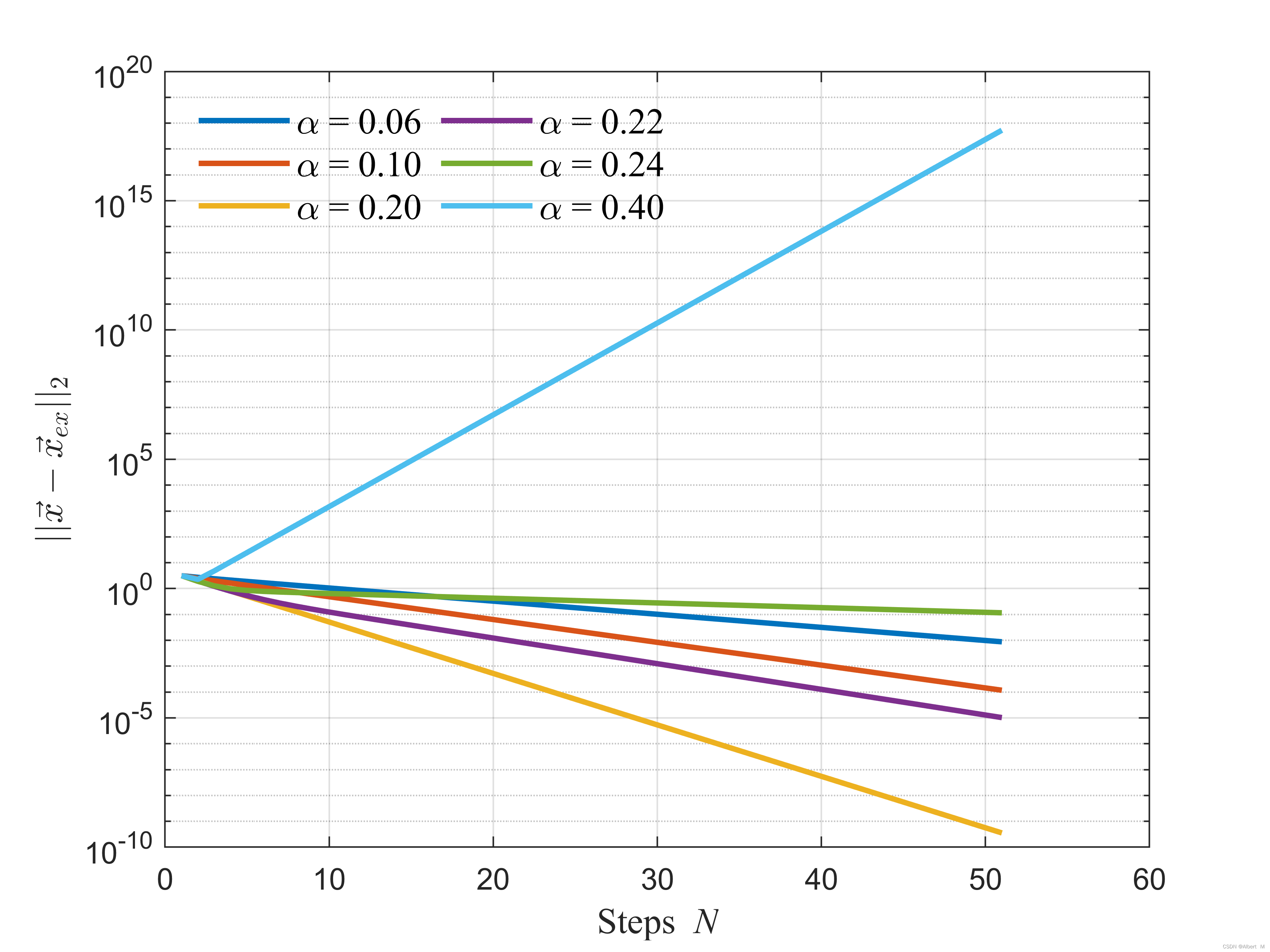
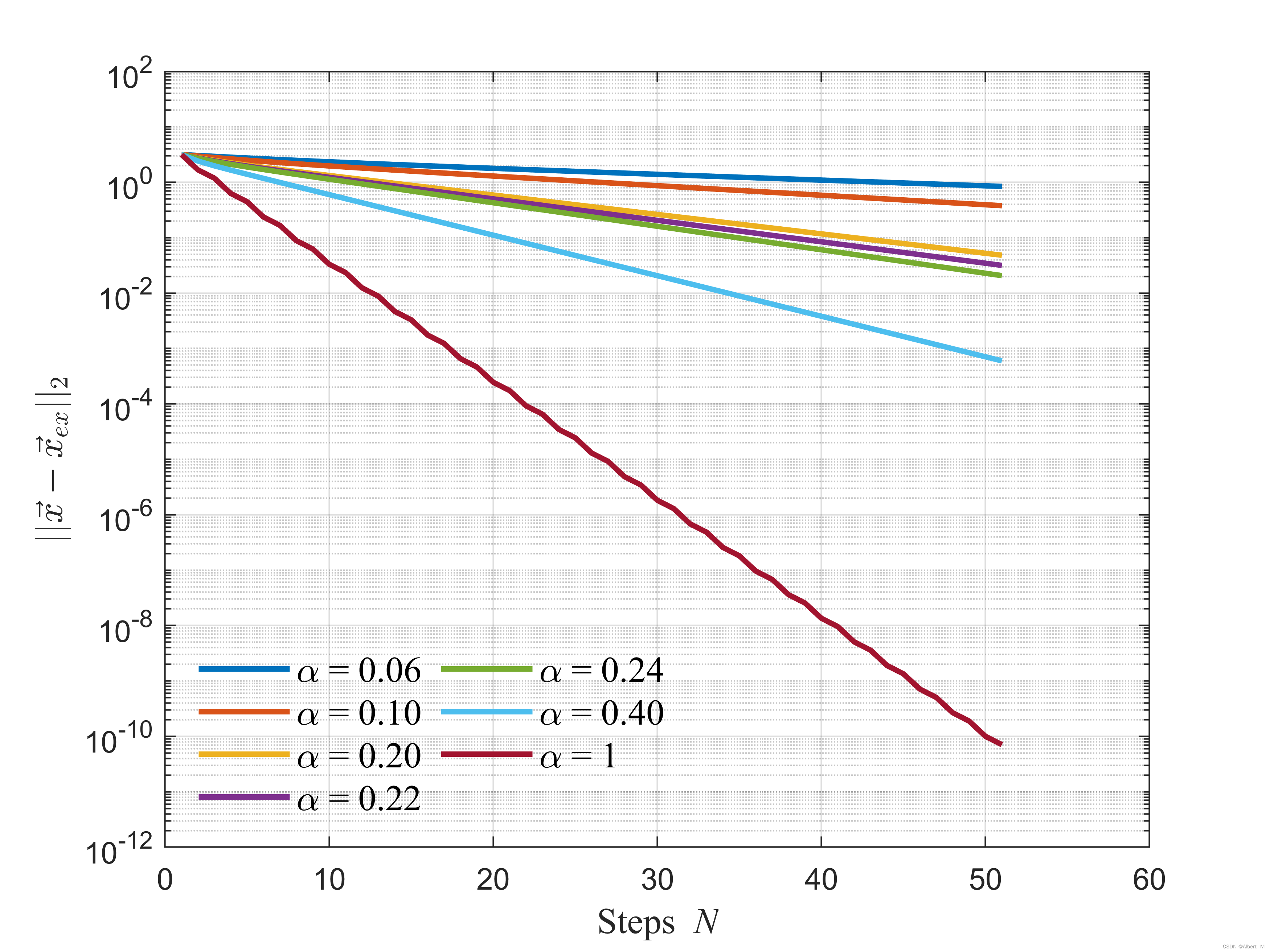
计算结果,如图所示:
结果与预期一致:
- 当 α = 0.4 > 0.245 \alpha=0.4>0.245 α=0.4>0.245 时,Richardson迭代法发散,其余算例均收敛;
- 当 α = 0.2 \alpha=0.2 α=0.2 时,Richardson迭代法收敛速度较其它算例更快;
观察收敛曲线可知,随着迭代的进行误差的对数与步数间逐渐线性化,这该如何解释?
实事上,收敛曲线的斜率满足:
从收敛曲线后半段斜率的几何意义上,我们也可以更好的理解为什么要求:
ρ
(
B
)
=
ρ
(
E
−
α
A
)
<
1
\rho(\bold B)=\rho(\bold E-\alpha\bold A)<1
ρ(B)=ρ(E−αA)<1
且越小越好。为说明Richardson迭代法也适用于非对称系数矩阵的线性方程组求解,对上述算例进行雅可比左预处理,即
[
1
6
0
0
1
4
]
[
6
3
3
4
]
[
x
1
x
2
]
=
[
1
6
0
0
1
4
]
[
−
3
−
9
]
⟺
[
1
1
2
3
4
1
]
[
x
1
x
2
]
=
[
−
1
2
−
9
4
]
\begin{bmatrix} \frac{1}{6} & 0 \\\\ 0 & \frac{1}{4} \end{bmatrix} \begin{bmatrix} 6 & 3 \\\\ 3 & 4 \end{bmatrix} \begin{bmatrix} x_1 \\\\ x_2 \end{bmatrix} =\begin{bmatrix} \frac{1}{6} & 0 \\\\ 0 & \frac{1}{4} \end{bmatrix} \begin{bmatrix} -3 \\\\ -9 \end{bmatrix} \Longleftrightarrow \begin{bmatrix} 1 & \frac{1}{2} \\\\ \frac{3}{4} & 1 \end{bmatrix} \begin{bmatrix} x_1 \\\\ x_2 \end{bmatrix} =\begin{bmatrix} -\frac{1}{2} \\\\ -\frac{9}{4} \end{bmatrix}
⎣
⎡610041⎦
⎤⎣
⎡6334⎦
⎤⎣
⎡x1x2⎦
⎤=⎣
⎡610041⎦
⎤⎣
⎡−3−9⎦
⎤⟺⎣
⎡143211⎦
⎤⎣
⎡x1x2⎦
⎤=⎣
⎡−21−49⎦
⎤
显然,这个与原方程有相同解的新方程组的系数矩阵非对称。对于新方程而言,系数矩阵的特征值为:
λ
⃗
A
′
=
[
1.6124
0.3876
]
T
\vec{\lambda}^{A'}=\begin{bmatrix}1.6124&0.3876\end{bmatrix}^T
λA′=[1.61240.3876]T
使得Richardson迭代法收敛的参数
α
\alpha
α 的取值范围为:
0
<
α
<
2
λ
m
a
x
A
′
=
1.24
0<\alpha<\frac{2}{\lambda^{A'}_{max}}=1.24
0<α<λmaxA′2=1.24
且有:
α
o
p
t
=
2
λ
m
a
x
A
′
+
λ
m
i
n
A
′
=
1
ρ
o
p
t
=
λ
m
a
x
A
′
−
λ
m
i
n
A
′
λ
m
a
x
A
′
+
λ
m
i
n
A
′
=
0.6124
\alpha_{opt}=\frac{2}{\lambda^{A'}_{max}+\lambda^{A'}_{min}}=1\\\ \\ \rho_{opt}=\frac{\lambda^{A'}_{max}-\lambda^{A'}_{min}}{\lambda^{A'}_{max}+\lambda^{A'}_{min}}=0.6124
αopt=λmaxA′+λminA′2=1 ρopt=λmaxA′+λminA′λmaxA′−λminA′=0.6124
实际计算结果如图: