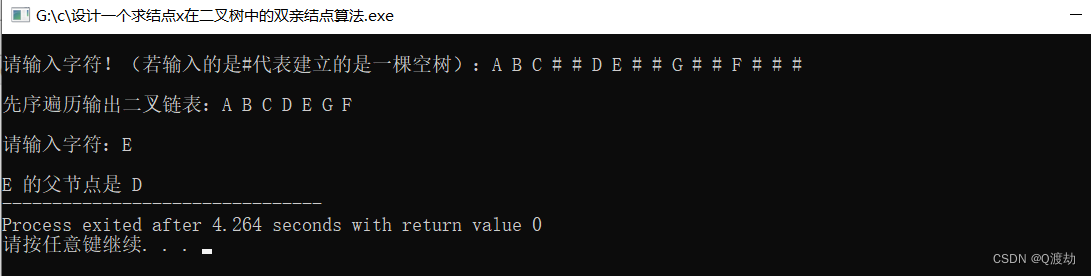
1、算法思想
使用先序递归遍历思想完成算法设计。首先判断节点的左右孩子是否存在,若存在,并且左右孩子中有一个符合查找要求,则返回元素!否则,继续递归查找,直到成功或者找不到符合要求的结点!
2、算法实现
——————————————————————————————————————————————————
#include<stdio.h>
#define MaxSize 20
#include
#include<stdlib.h>
#define endl ‘\n’
using namespace std;
typedef struct BiTNode{ //结点
char data; //数据域
struct BiTNode *lchild,*rchild; //指针域
}BiTNode,*BiTree;
——————————————————————————————————————————————————
//先序遍历的顺序建立二叉链表
void CreateTree(BiTree &T){
char ch;
cin>>ch;
if (ch == ‘#’) T = NULL; //递归结束,建立空树
else{
T = new BiTNode; //申请一个结点
T->data = ch; //将输入值赋值给T
CreateTree(T->lchild); //递归创建左子树
CreateTree(T->rchild); //递归创建右子树
}
}
——————————————————————————————————————————————————
//先遍历输出
void PreOrder(BiTree T){
if(T != NULL){
cout<data<<" “; //递归打印当前节点
PreOrder(T->lchild); //递归输出左子树
PreOrder(T->rchild); //递归输出右子树
}
}
——————————————————————————————————————————————————
//查找函数
void FindParents(BiTree T,char x){
if(T != NULL){
if(T->lchild != NULL && T->lchild->data == x) cout<<”\n"<<x<<" 的父节点是"<data;
if(T->rchild != NULL && T->rchild->data == x) cout<<“\n”<<x<<" 的父节点是"<data;;
FindParents(T->lchild,x);
FindParents(T->rchild,x);
}
}
——————————————————————————————————————————————————
//主函数
main(){
BiTree T;
cout<<“\n请输入字符!(若输入的是#代表建立的是一棵空树):”;
CreateTree(T);
cout<<“\n先序遍历输出二叉链表:”; //A B C # # D E # # G # # F # # #
//ABC##DE##G##F###
PreOrder(T);
fflush(stdin);
char x;
cout<<“\n\n请输入字符:”;
scanf(“%c”,&x);
FindParents(T,x);
}
——————————————————————————————————————————————————
3、核心代码
//查找函数
void FindParents(BiTree T,char x){
if(T != NULL){
if(T->lchild != NULL && T->lchild->data == x) cout<<"\n"<<x<<" 的父节点是"<<T->data;
if(T->rchild != NULL && T->rchild->data == x) cout<<"\n"<<x<<" 的父节点是"<<T->data;;
FindParents(T->lchild,x);
FindParents(T->rchild,x);
}
}
4、算法分析
该算法的实现是借助二叉树的先序遍历。递归遍历二叉树,每一次递归调用首先利用先序遍历判断当前根节点是否存在左右孩子,若是存在并且左右中的数值就是所给参数的孩子结点,那么当前父节点肯定是所给孩子结点的父亲节点,直接使用return返回当前参数结点的父亲节点,强行退出递归调用栈,程序执行完毕!否则继续递归调用二叉树,直到查找成功或者失败!