3. 神经网络与深度学习
3.1 Fashion-MNIST 数据集
3.1.1 Fashion-MNIST数据集
- MNIST是非常著名的手写数字数据集 (M:Modify; NIST: National Institute of Standard and Technology)
- MNIST中共有7万张图像:6万张用于训练;1万张用于测试;共0—9十个类别
- Fashion-MNIST数据集来自Zalando网站:10类别对应10种服饰;7万张 28x28的灰度图像
- Fashion-MNIST的目的是取代MNIST数据集,用作基准来测试机器学习算法
- Fashion-MNIST与MNIST数据集的异同:(1)异:MNIST数据集中图像都是手写图像,而Fashion-MNIST中的是真实图像;(2)同:这两个数据集具有相同的数据规模,图像大小,数据格式,以及训练集和测试集的分割方式
- MNIST为何如此受欢迎:1.该数据集的规模允许深度学习研究者快速地检查和复现它们的算法;2.在所有的深度学习框架中都能使用该数据集
- Pytorch中的torchvision包可以加载fashion-mnist数据集
3.2 使用torchvision导入和加载数据集
3.2.1 创建深度学习项目的流程:
- 准备数据集
- 创建网络模型
- 训练网络模型
- 分析结果
3.2.2 数据准备遵守ETL过程:
- 提取(extract)、转换(transform)、加载(load)
- pytorch中自带的包,能够将ETL过程变得简单
3.2.3 数据的准备(ETL):
- 1.提取(exact):从源数据中获取fashion-mnist图像数据
- 2.转换(transform):将数据转换成张量的形式
- 3.加载(load):将数据封装成对象,使其更容易访问
-
- Fashion-MNIST 与 MNIST数据集在调用上最大的不同就是URL的不同
-
- torch.utils.data.Dataset:一个用于表示数据集的抽象类
-
- torch.utils.data.DataLoader: 包装数据集并提供对底层的访问
import torch
import torchvision
import torchvision.transforms as transforms # 可帮助对数据进行转换
train_set = torchvision.datasets.FashionMNIST(
root = './data/FashionMNIST', # 数据集在本地的存储位置
train = True, # 数据集用于训练
download = True, # 如果本地没有数据,就自动下载(exact)
transform = transforms.Compose([
transforms.ToTensor()
]) # 将图像转换成张量(transform)
)
train_loader = torch.utils.data.DataLoader(train_set, batch_size=10)
# 训练集被打包或加载到数据加载器中,可以以我们期望的格式来访问基础数据;(load)
# 数据加载器使我们能够访问数据并提供查询功能3.3 数据集的访问
import numpy as np
import matplotlib.pyplot as plt
torch.set_printoptions(linewidth=120) # 设置打印行宽
print(len(train_set))
print(train_set.train_labels)
print(train_set.train_labels.bincount()) # bincount:张量中每个值出现的频数
## 都是6000 -》数据集与对应类的样本数是一致的 -》平衡数据集打印结果:
60000 tensor([9, 0, 0, ..., 3, 0, 5]) tensor([6000, 6000, 6000, 6000, 6000, 6000, 6000, 6000, 6000, 6000])
- 要想从训练集对象中访问一个单独的元素,首先要将一个训练集对象(train_set)传递给python的iter()函数,以此返回一个表示数据流的对象;然后就可以使用next函数来获取数据流中的元素
# 查看单个样本
sample = next(iter(train_set))
print(len(sample))
print(type(sample))
# 将sample解压成图像和标签(解构对象)
image = sample[0]
label = sample[1]
image.shape
# 显示图像和标签
plt.imshow(image.squeeze(), cmap='gray') # squezz()将[1, 28, 28]->[28,28]
print('label:', label)打印结果:
2 <class 'tuple'>
torch.Size([1, 28, 28])
label: 9
# 查看批量样本
batch= next(iter(train_loader))
print(len(batch))
print(type(batch))
images, labels = batch
print(images.shape) # 之前 train_loader 设置了 batch_size=10(一批有10个样本)
print(labels.shape)打印结果:
2 <class 'list'> torch.Size([10, 1, 28, 28]) torch.Size([10])
# 画出一批的图像
grid= torchvision.utils.make_grid(images,nrow =10) # 设置一行放10张,make_grid() -》将多幅图像设置成一幅
print(grid.shape)
plt.figure(figsize=(15, 15)) # figsize设置幕布大小尺寸
plt.imshow(np.transpose(grid,(1,2,0))) # 使轴满足图像功能所需规格(交换坐标轴) (0,1,2)->(x,y,z) ==> (1,2,0)->(y,z,x)
print('labels:', labels)
# 可以通过改变batchsize来显示更多的数据torch.Size([3, 32, 302]) labels: tensor([9, 0, 0, 3, 0, 2, 7, 2, 5, 5])
3.4 网络建立
3.4.1 class和object的区分
- class 就是一个实际对象的蓝图或描述
- object 就是事物本身
- 创建的对象需要在类的实例中调用对象
-
- 一个给定类的所有实例都有两个核心组件:方法和属性
-
- 方法代表代码,属性代表数据;方法和属性是由类定义的
-
- 属性用于描述对象的特征;方法用于描述对象的行为,即对象能够做什么
-
- 在一个项目中可以有许多对象,即给定类的实例可以同时存在(可在一个类中创建多个对象)
-
- 类用于封装方法和属性
3.4.2 类和实例(对象)<python基础知识补充>
- 类是抽象的模板,用于表述具有相同属性和方法的对象的集合,类的命名尽量见名知意
- 对象是真实的,见得到摸得着的东西
- 类的定义:class 类名():
- 类的组成:类名;属性(一组数据);方法(允许进行的操作)
# 类的创建
class Lizard:
def __init__(self, name): # 创建对象时自动运行,不用额外调用,无返回值
self.name = name
def set_name(self, name):
self.name = name
# 类的调用
lizard = Lizard('deep')
print(lizard.name) # deep
lizard.set_name('lizard')
print(lizard.name) # lizard3.4.3 面向对象编程与pytorch的结合
- 构建一个神经网络的主要组件是层(pytorch神经网络库中包含了帮助构造层的类)
- 神经网络中的每一层都有两个主要组成部分:转换和权重(转换代表代码;权重代表数据)
- forward方法(前向传输):张量通过每层的变换向前流动,直到达到输出层
- 构建神经网络时必须提供前向方法,前向方法即为实际的变换
- 使用pytorch创建神经网络的步骤:
- 1.扩展nn.Module基类
- 2.定义层(layers)为类属性
- 3.实现前向方法
# CNN网络的建立
import torch.nn as nn
class Network(nn.Module): #()中加入nn.Module可以使得Network类继承Module基类中的所有功能
def __init__(self):
super(Network, self).__init__() # 对继承的父类的属性进行初始化,使用父类的方法来进行初始化
self.conv1 = nn.Conv2d(in_channels=1, out_channels=6, kernel_size=5) #in_channels=1(灰度图像)
self.conv2 = nn.Conv2d(in_channels=6, out_channels=12, kernel_size=5)#in_channels=6(上一层的out),即上一层的输出是这一层的输入
self.fc1 = nn.Linear(in_features=12*4*4, out_features=120) # 从卷积层传入线性层需要对张量flatten(4*4)
self.fc2 = nn.Linear(in_features=120, out_features=60)
self.out = nn.Linear(in_features=60, out_features=10) #out_channels=10(形成图像最后的10个类别)
def forward(self, t):
# implement the forward pass
return t
network = Network() # 创建网络对象networkNetwork( (conv1): Conv2d(1, 6, kernel_size=(5, 5), stride=(1, 1)) (conv2): Conv2d(6, 12, kernel_size=(5, 5), stride=(1, 1)) (fc1): Linear(in_features=192, out_features=120, bias=True) (fc2): Linear(in_features=120, out_features=60, bias=True) (out): Linear(in_features=60, out_features=10, bias=True) )
3.5 CNN构建及网络参数的使用
在上述的Network类中,我们定义了两个卷积层和一个线性层;两个主要的部分封装在其中,即前向函数的定义和权重张量;每个层中权重张量包含了随着我们的网络在训练过程中学习而更新的权重值(这就是在网络类中将层定义为类属性的原因);在Module类中,pytorch可以跟踪每一层的权重张量,由于我们在创建Network类时扩展了Module类,也就自动继承了该功能。
- Parameter和Argument的区别:
-
- Parameter在函数定义中使用,可将其看作是占位符;(形参)
-
- Argument是当函数被调用时传递给函数的实际值;(实参)
- Parameter的两种类型:
- 1.Hyperparameters:其值是手动和任意确定的;要构建神经网络:kernel_size, out_channels, out_features都需要手动选择
- 2.Data dependent Hyperparameters:其值是依赖于数据的参数
-
- 该参数位于网络的开始或末端,即第一个卷积层的输入通道和最后一个卷积层的输出特征图
-
- 第一个卷积层的输入通道依赖于构成训练集的图像内部的彩色通道的数量(灰度图像是1,彩色图像是3)
-
- 输出层的输出特征依赖于训练集中类的数量(fashion-MNIST数据集中的类型为10,则输出层的out_features=10)
-
- 通常情况下,一层的输入是上一层的输出(即:卷积层中所有输入通道和线性层中的输入特征都依赖于上一层的数据)
- 当张量从卷积层传入线性层时,张量必须是flatten的
| Parameter | Description |
|---|---|
| kernel_size | 设置滤波器的大小;滤波器的数量就是输出通道数 |
| out_channels | 设置滤波器的数量,即为输出通道数 |
| out_features | 设置输出张量的大小 |
3.6 CNN的权重
- 可学习参数:是在训练过程中学习的参数,初值是选择的任意值,其值在网络学习的过程中以迭代的方式进行更新
- 说网络在学习是指:网络在学习参数的适合的值,适合的值就是能使损失函数最小化的值
- 可学习的参数是网络的权重,存在于每一层中
- 当我们扩展类的时候,我们会得到它的所有功能,为了得到它,我们可以添加额外的功能,也可覆盖现有的功能
- 在python中,所有特殊的面向对象的方法通常都有前双下划线和后双下划线(init, __repr__)
- 如下所示,在未扩展module时,基类会返回默认字符串表示,我们可重写__repr__函数输出想要字符串
import torch.nn as nn
class Network():
def __init__(self):
#super(Network, self).__init__()
self.conv1 = nn.Conv2d(in_channels=1, out_channels=6, kernel_size=5)
self.conv2 = nn.Conv2d(in_channels=6, out_channels=12, kernel_size=5)
self.fc1 = nn.Linear(in_features=12*4*4, out_features=120)
self.fc2 = nn.Linear(in_features=120, out_features=60)
self.out = nn.Linear(in_features=60, out_features=10)
def forward(self,t):
# implement the forward pass
return t
def __repr__(self):
return "lizard"
network = Network() # lizard- 可使用点符号来访问指定的层
network.conv1
network.fc1Conv2d(1, 6, kernel_size=(5, 5), stride=(1, 1))
Linear(in_features=192, out_features=120, bias=True)
kernel_size=(5, 5) # 内核大小,即滤波器的高宽
stride=(1, 1) # 步长,构造函数没设置时,层会自动设置,表示每次操作之后滤波器应该滑动的距离(向右和向下一个单位)
bias=True # 线性层的偏差- 输出权重形状
# 输出conv1权重的形状
network.conv1.weight.shape # torch.Size([6, 1, 5, 5])
conv1 = nn.Conv2d(in_channels=1, out_channels=6, kernel_size=5)
# torch.Size([6, 1, 5, 5]) # 6个滤波器,1个输入通道,每个滤波器是5*5的
conv2 = nn.Conv2d(in_channels=6, out_channels=12, kernel_size=5)
# torch.Size([12, 6, 5, 5]) # 12个滤波器,滤波器深度为6(一次可以划过6个输入通道),每个滤波器是5*5的
network.conv2.weight[0].shape
# 单独的一个滤波器,形状是(深度,高,宽)torch.Size([6, 5, 5])
# 对于线性层或全连接层,由于需要flatten的张量输入,故此时的权重张量是个秩为2的高度、宽度轴
network.fc1.weight.shape # height=>out_features; width=>in_features
fc1 = nn.Linear(in_features=12*4*4, out_features=120)
# torch.Size([120, 192]) # 高度是输出特征的长度,宽度是输入特征的长度- 为了追踪网络中的所有权重张量,pytorch有一个叫Parameter的类,该类扩展了Tensor类, 所以每一层的权重张量就是这个参数类的一个实例
- 权重矩阵定义了线性函数(线性映射)
# 访问所有的参数
# 方法1:
for param in network.parameters():
print(param.shape)
torch.Size([6, 1, 5, 5]) torch.Size([6]) torch.Size([12, 6, 5, 5]) torch.Size([12]) torch.Size([120, 192]) torch.Size([120]) torch.Size([60, 120]) torch.Size([60]) torch.Size([10, 10]) torch.Size([10])
# 方法2:
for name, param in network.named_parameters():
print(name,'\t\t', param.shape)conv1.weight torch.Size([6, 1, 5, 5]) conv1.bias torch.Size([6]) conv2.weight torch.Size([12, 6, 5, 5]) conv2.bias torch.Size([12]) fc1.weight torch.Size([120, 192]) fc1.bias torch.Size([120]) fc2.weight torch.Size([60, 120]) fc2.bias torch.Size([60]) out.weight torch.Size([10, 10]) out.bias torch.Size([10])
3.7 pytorch可调用模块
3.7.1 Linear的工作原理
使用一个权重矩阵将输入特征空间映射到一个输出特征空间(矩阵乘法)
[1,2,3,4] -> [30., 40., 50.]
# 矩阵乘法
in_features = torch.tensor([1,2,3,4], dtype=torch.float32)
weight_matrix = torch.tensor([
[1,2,3,4],
[2,3,4,5],
[3,4,5,6]
], dtype = torch.float32)
weight_matrix.matmul(in_features)# 线性层
fc = nn.Linear(in_features=4, out_features=3)
# pytorch 线性层通过将数字4和3传递给构造函数,会自己创建一个3x4的权重矩阵
# 查看in_features张量
fc(in_features)
# 此时的结果与上述不同是因为这里的weight_matrix是由随机值来初始化的
tensor([-1.4051, -1.1374, 1.6383], grad_fn=<AddBackward0>)
# 在parameter类中包装一个权重矩阵,以使得输出结果与前面矩阵相乘一样
fc = nn.Linear(in_features=4, out_features=3)
fc.weight= nn.Parameter(weight_matrix)
fc(in_features)
# 此时的结果接近,却不精确,是因为由bias的存在
# tensor([30.4911, 39.7467, 49.7023], grad_fn=<AddBackward0>)
# 给bias传递一个false值,以得到精确的输出
fc = nn.Linear(in_features=4, out_features=3, bias =False)
fc.weight = nn.Parameter(weight_matrix)
fc(in_features)
# tensor([30., 40., 50.], grad_fn=<SqueezeBackward3>)- 线性转换的数学表示:
- y = Ax + b
- A: 权重矩阵张量
- x: 输入张量
- b: 偏差张量
- y: 输出张量
3.7.2 特殊的调用
- 调用对象实例时,调用特殊调用方法__call__,它会与我们的层layer与网络前向方法forward相互作用。
- 我们不直接调用前向方法,而是调用对象实例,之后调用方法会在pytorch下调用,而调用方法反过来调用我们的前向方法。
3.8 CNN前向方法的实现
- 前向方法的实现将使用我们在构造函数中定义的所有层
- 前向方法实际上是输入张量到预测的输出张量的映射
3.8.1 Input Layer
- 输入层是由输入数据决定的
- 输入层可以看做是恒等变换 f(x)=x
- 输入层通常是隐式存在的
import torch.nn as nn
import torch.nn.functional as F
class Network(nn.Module):
def __init__(self):
super(Network, self).__init__()
self.conv1 = nn.Conv2d(in_channels=1, out_channels=6, kernel_size=5)
self.conv2 = nn.Conv2d(in_channels=6, out_channels=12, kernel_size=5)
self.fc1 = nn.Linear(in_features=12*4*4, out_features=120)
self.fc2 = nn.Linear(in_features=120,out_features=60)
self.out = nn.Linear(in_features=60, out_features=10)
def forward(self,t):
# (1) input layer
t = t
# (2) hidden conv layer1
t = self.conv1(t)
t = F.relu(t)
t = F.max_pool2d(t, kernel_size=2, stride=2)
# (3) hidden conv layer2
t = self.conv2(t)
t = F.relu(t)
t = F.max_pool2d(t, kernel_size=2, stride=2)
# relu 和 max pooling 都没有权重;激活层和池化层的本质都是操作而非层;层与操作的不同之处在于,层有权重,操作没有
#(4)hidden linear layer2
t = t.reshape(-1, 12*4*4) # 全连接层要展开
t = self.fc1(t)
t = F.relu(t)
# (5) hidden linear layer2
t = self.fc2(t)
t = F.relu(t)
# (6) output layer
t = self.out(t)
# t= F.softmax(t, dim=1) # 这里暂不使用softmax,在训练中使用交叉熵损失可隐式的表示softmax
# 在隐藏层中,通常使用relu作为非线性激活函数
# 在输出层,有类别要预测时,使用softmax激活函数3.9 单张图像的预测
3.9.1 前向传播(forward propagation)
- 是将输入张量转换为输出张量的过程(即:神经网络是将输入张量映射到输出张量的函数)
- 前向传播只是将输入张量传递给网络并从网络接收输出的过程的一个特殊名称
3.9.2 反向传播(back propagation)
- 反向传播通常在前向传播后发生
- 使用torch.set_grad_enabled(False)来关闭pytorch的梯度计算,这将阻止pytorch在我们的张量通过网络时构建一个计算图
- 计算图通过跟踪张量在网络中传播的每一个计算,来跟踪网络的映射;然后在训练过程中使用这个图来计算导数,也就是损失函数的梯度;关闭并非强制的,但可以减少内存。
# 单张图像预测
import torch
import torch.nn as nn
import torch.nn.functional as F
import torchvision
import torchvision.transforms as transforms
# 设置打印格式
torch.set_printoptions(linewidth=120)
# 一、数据准备
train_set = torchvision.datasets.FashionMNIST(
root = './data/FashionMNIST'
,train = True
,download = True
, transform = transforms.Compose([
transforms.ToTensor()
])
)
# 二、创建网络
class Network(nn.Module):
def __init__(self):
super(Network, self).__init__()
self.conv1 = nn.Conv2d(in_channels = 1, out_channels=6, kernel_size=5)
self.conv2 = nn.Conv2d(in_channels = 6, out_channels=12, kernel_size=5)
self.fc1 = nn.Linear(in_features = 12*4*4, out_features=120)
self.fc2 = nn.Linear(in_features = 120, out_features = 60)
self.out = nn.Linear(in_features = 60, out_features=10)
def forward(self, t):
# (1)Input Layer
t = t
# (2) hidden conv1
t = self.conv1(t)
t = F.relu(t)
t = F.max_pool2d(t, kernel_size=2, stride=2)
# (3) hidden conv2
t = self.conv2(t)
t = F.relu(t)
t = F.max_pool2d(t, kernel_size=2, stride=2)
# (4) hidden linear1
t = t.reshape(-1, 12*4*4)
t = self.fc1(t)
t = F.relu(t)
# (5) hidden linear2
t = self.fc2(t)
t = F.relu(t)
# (6) output
t = self.out(t)
return t
# 调用network实例
torch.set_grad_enabled(False) #关闭pytorch的梯度计算
network = Network()
sample = next(iter(train_set))
image, label = sample
print(image.shape)
# 显示图像和标签
#plt.imshow(image.squeeze(), cmap='gray') # 将[1, 28, 28]->[28,28]
#print('label:', label)
# 如上我们得到的图像的形状为[1,28,28];而网络期望的张量是【batchsize,channels, height, width】
# 需要使用unsqueeze方法来为其增加一个维度,使批大小为1,即[1,1,28,28]
print(image.unsqueeze(0).shape)
# 对单张图像进行预测
pred = network(image.unsqueeze(0))
print(pred.shape) # [1,10] 批处理中有一个图像,10个预测类
print(pred.argmax(dim=1)) # 最高值出现在[2],也就是预测为套衫
print(label) # 实际标签为9,即靴子结果:
torch.Size([1, 28, 28]) torch.Size([1, 1, 28, 28]) torch.Size([1, 10]) tensor([2]) 9
# 要想将预测值用概率表示,可以使用softmax
print(pred)
print(F.softmax(pred, dim=1))
print(F.softmax(pred, dim=1).sum())tensor([[ 0.1015, 0.0297, 0.1688, -0.1035, 0.0376, -0.0852, 0.0326, 0.0632, -0.0752, -0.0850]]) tensor([[0.1093, 0.1018, 0.1169, 0.0891, 0.1026, 0.0907, 0.1021, 0.1052, 0.0916, 0.0907]]) tensor(1.0000)
3.10 单批次图像预测
import torch
import torch.nn
import torch.nn.functional as F
import torchvision
import torchvision.transforms as transforms
torch.set_printoptions(linewidth=120)
# 数据准备
train_set = torchvision.datasets.FashionMNIST(
root = './data/FashionMNIST'
,train = True
,download = True
,transform = transforms.Compose([
transforms.ToTensor()
]))
# 网络创建
class Network(nn.Module):
def __init__(self):
super(Network, self).__init__()
self.conv1 = nn.Conv2d(in_channels=1, out_channels=6, kernel_size=5)
self.conv2 = nn.Conv2d(in_channels=6, out_channels=12, kernel_size=5)
self.fc1 = nn.Linear(in_features=12*4*4, out_features=120)
self.fc2 = nn.Linear(in_features=120, out_features=60)
self.out = nn.Linear(in_features=60, out_features=10)
def forward(self, t):
#super(Network, self).__init__()
#(1)Input Layer
t = t
#(2)Conv1
t = F.relu(self.conv1(t))
t = F.max_pool2d(t, kernel_size=2, stride=2)
#(3)Conv2
t = F.relu(self.conv2(t))
t = F.max_pool2d(t, kernel_size=2, stride=2)
#(4)FC1
t = t.reshape(-1,12*4*4)
t = F.relu(self.fc1(t))
#(5)FC2
t = F.relu(self.fc2(t))
#(6)output
t = self.out(t)
return t
# 调用network实例
torch.set_grad_enabled(False)
network = Network()
# 从dataloader中取出一批数据
data_loader = torch.utils.data.DataLoader(train_set, batch_size=10)
batch = next(iter(data_loader))
images, labels = batch
print(images.shape) # 一批有10个图像,有1个彩色通道,高度宽度都为28
print(labels.shape) # 10个标签
preds = network(images)
print(preds.shape) # 10张图片,10个预测类
print(preds.argmax(dim=1)) # 找每行最大值索引,即预测出来属于哪个标签
print(labels) # 图像本身的标签
#tensor([0, 6, 6, 6, 6, 6, 0, 6, 6, 0])
#tensor([9, 0, 0, 3, 0, 2, 7, 2, 5, 5])
preds.argmax(dim=1).eq(labels) # 预测类别与标签匹配,就置为1,true
#tensor([False, False, False, False, False, False, False, False, False, False])
preds.argmax(dim=1).eq(labels).sum() # 计算总共有几个预测成功 0
- 可以设置一个函数来接受预测张量和标签张量,然后使用item方法返回预测数
def get_num_corret(preds,label):
return preds.argmax(dim=1).eq(labels).sum().item()
get_num_corret(preds,label) # 03.11 输入张量在通过CNN的过程中的变化
3.11.1 CNN 输出特征图尺寸(正方形)
- 假设输入特征的大小为n x n
- 假设滤波器的大小为 f x f
- 令padding为p,步长stride为s
- 则输出特征图的大小为 O = ( n - f + 2p )/s + 1
3.11.2 CNN 输出特征图尺寸(非正方形)
- 假设输入特征的大小为 nh x nw
- 假设滤波器的大小为 fh x fw
- 令padding为p,步长stride为s
- 则输出特征图的高度为 Oh = (nh - fh + 2p)/s + 1
- 输出特征图的宽度为 Ow = (nw - fw + 2p)/s + 1
[1,1,28,28]
-
convolution(55) O = (28-5+20)/1 + 1 = 24 [1,6,24,24]
-
max pooling(22) O = (24-2+20)/2 + 1 = 12 [1,6,12,12]
-
convolution(55) O = (12-5+20)/1 + 1 = 8 [1,12,8,8]
-
max pooling(22) O = (8-2+20)/2 + 1 = 4 [1,12,4,4]
-
这就是为什么展开时要12*4*4
3.12 训练神经网络的步骤
3.12.1 训练神经网络的七个步骤
- 从训练集中获取批量数据
- 将批量数据传入网络
- 计算损失(预测值与真实值之间的差)【需要loss function实现】
- 计算损失函数的梯度 【需要back propagation实现】
- 通过上一步计算的梯度来更新权重,进而减少损失【需要optimization algorithm实现】
- 重复1-5步直到一个epoch执行完成
- 重复1-6步直到所设定的epochs执行完成并得到满意的accuracy
3.12.2 单批次图像训练
3.12.3 单周期(epoch)CNN的训练
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
import torchvision
import torchvision.transforms as transforms
torch.set_printoptions(linewidth=120) # 设置打印行款
torch.set_grad_enabled(True)
# 数据准备
train_set = torchvision.datasets.FashionMNIST(
root = './data/FashionMNIST',
train = True,
download = True,
transform = transforms.Compose([transforms.ToTensor()
]))
# 创建网络
class Network(nn.Module):
def __init__(self):
super(Network,self).__init__()
self.conv1 = nn.Conv2d(in_channels=1, out_channels=6, kernel_size=5)
self.conv2 = nn.Conv2d(in_channels=6, out_channels=12, kernel_size=5)
self.fc1 = nn.Linear(in_features= 12*4*4, out_features=120)
self.fc2 = nn.Linear(in_features= 120, out_features=60)
self.out = nn.Linear(in_features=60, out_features=10)
def forward(self, t):
t = t
t = F.relu(self.conv1(t))
t = F.max_pool2d(t, kernel_size =2, stride=2)
t = F.relu(self.conv2(t))
t = F.max_pool2d(t, kernel_size=2, stride=2)
t = t.reshape(-1, 12*4*4)
t = F.relu(self.fc1(t))
t = F.relu(self.fc2(t))
t = self.out(t)
return t
# 定义函数用于计算预测正确的数目
def get_num_correct(preds, labels):
return preds.argmax(dim=1).eq(labels).sum().item()
# 创建网络实例,进行单周期训练
network = Network()
train_loader = torch.utils.data.DataLoader(train_set, batch_size=100)
# 优化器
optimizer = optim.Adam(network.parameters(), lr=0.01)
for epoch in range(2): #进行两个周期
total_loss = 0
total_correct = 0
for batch in train_loader: #使所有批次进入循环
images, labels =batch
#计算损失
preds = network(images)
loss = F.cross_entropy(preds, labels) # 交叉熵损失函数
optimizer.zero_grad() #计算新批次梯度前,要把之前梯度归零,否则pytorch会累积梯度
loss.backward() #计算梯度,反向传播
optimizer.step() #更新权重
total_loss += loss.item()
total_correct += get_num_correct(preds, labels)
print("epoch:",epoch,"loss:",total_loss,"total_correct:",total_correct)
accuracy = total_correct/len(train_set) #准确率 51719/60000
print("accuracy:",accuracy)打印结果:
epoch: 0 loss: 324.95763002336025 total_correct: 47836 epoch: 1 loss: 224.75781846046448 total_correct: 51719 accuracy: 0.8619833333333333
- 每个周期的迭代数 = 数据总数/batchsize(当改变batchsize时,也就是改变了更新权重的次数,也就是朝损失函数最小的防线前进的步数)
- accuracy = total_correct/len(train_set)
- 梯度:告诉我们应该走哪条路能更快的到达loss最小
- 可以使用SGD或Adam优化更新权重
- 要传递网络的参数和学习速率lr。学习率是训练过程中的一个超参数,即告诉优化器朝着loss最小的方向走多远,因此不要走太远。
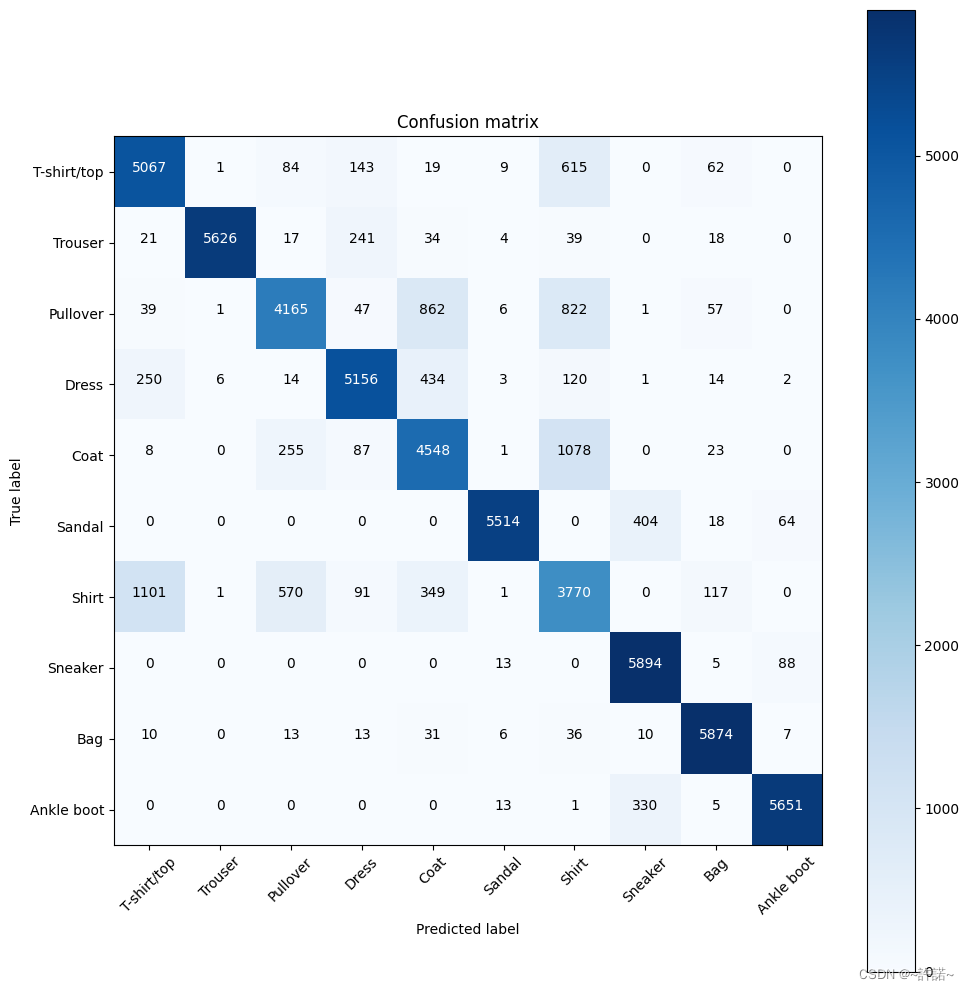
3.13 神经网络的混淆矩阵
- 创建混淆矩阵的两个条件:一个预测的张量和一个有相应真值或标签的张量
- 使用sklearn.metrics绘制混淆矩阵(方法2:)
import matplotlib.pyplot as plt
from sklearn.metrics import confusion_matrix
from resources.plotcm import plot_confusion_matrix # plotcm.py文件位于当前文件resources中
cm = confusion_matrix(train_set.targets, train_preds.argmax(dim=1))
print(type(cm))
# 绘图
names = (
'T-shirt/top',
'Trouser',
'Pullover',
'Dress',
'Coat',
'Sandal',
'Shirt',
'Sneaker',
'Bag',
'Ankle boot')
plt.figure(figsize=(10,10))
plot_confusion_matrix(cm, names)Confusion matrix, without normalization [[5067 1 84 143 19 9 615 0 62 0] [ 21 5626 17 241 34 4 39 0 18 0] [ 39 1 4165 47 862 6 822 1 57 0] [ 250 6 14 5156 434 3 120 1 14 2] [ 8 0 255 87 4548 1 1078 0 23 0] [ 0 0 0 0 0 5514 0 404 18 64] [1101 1 570 91 349 1 3770 0 117 0] [ 0 0 0 0 0 13 0 5894 5 88] [ 10 0 13 13 31 6 36 10 5874 7] [ 0 0 0 0 0 13 1 330 5 5651]]
3.14 concatenating和stacking的区分
- (拼接)concatenating是在一个现有的轴上连接一系列的张量
- (堆叠)stacking是在一个新的轴上连接一系列的张量(即,我们在所有的张量中创建一个新轴)