实验一:顺序表的实现及应用
- 实验实习目的及要求
实验目的:了解和掌握线性表的顺序存储结构;掌握用C语言上机调试线性表的基本方法;掌握线性表的基本操作:插入、删除、查找以及线性表合并等运算在顺序存储结构和链接存储结构上的运算,以及对相应算法的性能分析。
实验要求:1.程序改错。给定一段程序代码,程序代码所完成的功能为:(1)建立一个线性表;(2)依次输入数据元素1,2,3,4,5,6,7,8,9,10;(3)删除数据元素5;(4)依次显示当前线性表中的数据元素。假设该线性表的数据元素个数在最坏情况下不会超过100个,要求使用顺序表。2.编写合并函数,将两个有序线性表合并为一个有序表并在主函数中加以测试。
- 实验实习设备(环境)及要求(软硬件条件)
实验室B515,电脑。
- 实验实习项目、内容与步骤
1.改正程序中的错误。2.编写合并函数,将两个有序线性表合并为一个有序表并在主函数中加以测试。3.完成实验报告的撰写。
实验实习所得结果及分析
程序改错:
#include <stdio.h>
#define MaxSize 100
typedef int DataType;
typedef struct
{
DataType list[MaxSize];
int size;
} SeqList;
void ListInitiate(SeqList *L)/*初始化顺序表L*/
{
L->size = 0;/*定义初始数据元素个数*/
}
int ListLength(SeqList L)/*返回顺序表L的当前数据元素个数*/
{
return L.size;
}
int ListInsert(SeqList *L, int i, DataType x)
/*在顺序表L的位置i(0 ≤ i ≤ size)前插入数据元素值x*/
/*插入成功返回1,插入失败返回0*/
{
int j;
if(L->size >= MaxSize)
{
printf("顺序表已满无法插入! \n");
return 0;
}
else if(i < 0 || i > L->size )
{
printf("参数i不合法! \n");
return 0;
}
else
{ //此段程序有一处错误
for(j = L->size; j >= i; j--) L->list[j+1] = L->list[j];/*为插入做准备*/
L->list[i] = x;/*插入*/
L->size ++;/*元素个数加1*/
return 1;
}
}
int ListDelete(SeqList *L, int i, DataType *x)
/*删除顺序表L中位置i(0 ≤ i ≤ size - 1)的数据元素值并存放到参数x中*/
/*删除成功返回1,删除失败返回0*/
{
int j;
if(L->size <= 0)
{
printf("顺序表已空无数据元素可删! \n");
return 0;
}
else if(i < 0 || i > L->size-1)
{
printf("参数i不合法");
return 0;
}
else
{//此段程序有一处错误
*x = L->list[i];/*保存删除的元素到参数x中*/
for(j = i +1; j <= L->size-1; j++) L->list[j-1]=L->list[j];/*依次前移*/
L->size--;/*数据元素个数减1*/
return 1;
}
}
int ListGet(SeqList L, int i, DataType *x)
/*取顺序表L中第i个数据元素的值存于x中,成功则返回1,失败返回0*/
{
if(i < 0 || i > L.size-1)
{
printf("参数i不合法! \n");
return 0;
}
else
{
*x = L.list[i];
return 1;
}
}
int main(void)
{ SeqList myList;
int i , x;
ListInitiate(&myList);
for(i = 0; i < 10; i++)
ListInsert(&myList, i, i+1);
ListDelete(&myList, 4, &x);
for(i = 0; i < ListLength(myList); i++)
{
ListGet(myList,i,&x); //此段程序有一处错误
printf("%d", x);
}
}
运行结果:1234678910
线性表合并:
#include<stdio.h>
#define ListSize 100 //线性表的最大长度
typedef struct
{
int data[ListSize]; //用数组存储线性表中的元素
int length; //顺序表中元素的个数
}SeqList, *PSeqList;
void InitList(PSeqList L)
{
if (L == NULL)
{
return;
}
L->length = 0;
}
int GetData(PSeqList L, int i)
{
return L->data[i - 1];
}
int InsList(PSeqList L, int i,int e)
{
int k;
for (k = i; k <= L->length; k--)
{
L->data[k + 1] = L->data[k];
}
L->data[i - 1] = e;
L->length++; //数据表的长度加1
return 1;
}
void MergeList(SeqList &La, SeqList &Lb, SeqList &Lc)
{
int i=0, j=0,k=0;
int m = La.length;
int n = Lb.length;
while(j < n && i< m)
{
if (La.data[i]>Lb.data[j])
{
Lc.data[k] = Lb.data[j];
Lc.length++;
k++;
j++;
}
else
{
Lc.data[k] = La.data[i];
Lc.length++;
k++;
i++;
}
}
while (i < m) //B已到达表尾,依次将A的剩余元素插人C的最后
{
Lc.data[k] = La.data[i];
Lc.length++;
k++;
i++;
}
while (j < n) //A已到达表尾,依次将B的剩余元素插人C的最后
{
Lc.data[k] = Lb.data[j];
Lc.length++;
k++;
j++;
}
}
int main()
{
int n1,n2,n3;
int i,j,k;
SeqList La ,Lb,Lc;
InitList(&La); InitList(&Lb); InitList(&Lc);
printf("请输入A表和B表的长度:\n");
scanf("%d",&n1);
printf("A表有%d个元素\n",n1) ;
La.length=n1;
scanf("%d",&n2);
printf("B表有%d个元素\n",n2);
Lb.length=n2;
printf("输入A表元素:\n");
for(i=0;i<n1;i++)
{
scanf("%d",&La.data[i]);
}
printf("输入B表元素:\n");
for(j=0;j<n2;j++)
{
scanf("%d",&Lb.data[j]);
}
printf("合并前A表的元素为:\n");
for(i=0;i<n1;i++)
{
printf("%d ",La.data[i]);
}
printf("合并前B表的元素为:\n");
for(j=0;j<n2;j++)
{
printf("%d ",Lb.data[j]);
}
MergeList(La, Lb,Lc);
n3=Lc.length;
printf("合并后的C表为:");
for(k=0;k<n3;k++)
{
printf("%d ",Lc.data[k]);
}
return 0;
}
改错:
实验二:链表的实现及应用
一、实验实习目的及要求
实验目的:了解和掌握线性表的链式存储结构;掌握用C语言上机调试线性表的基本方法;掌握线性表的基本操作:插入、删除、查找以及线性表合并等运算在顺序存储结构和链接存储结构上的运算,以及对相应算法的性能分析。
实验要求:给定一段程序代码,程序代码所完成的功能为:(1)建立一个线性表;(2)依次输入数据元素1,2,3,4,5,6,7,8,9,10;(3)删除数据元素5;(4)依次显示当前线性表中的数据元素。假设该线性表的数据元素个数在最坏情况下不会超过100个,要求使用单链表。
二、实验实习设备(环境)及要求(软硬件条件)
实验室B515,电脑。
三、实验实习项目、内容与步骤
实验项目:顺序表的实现及应用
实验内容:掌握顺序表结构,实现其插入、删除等算法。利用顺序表将两个有序线性表合并为一个有序表。
实验步骤:1.改正程序中的错误。2.编写程序。
四、实验实习所得结果及分析
程序改错:
#include <stdio.h>/*该文件包含printf()等函数*/
#include <stdlib.h>/*该文件包含exit()等函数*/
#include <malloc.h>/*该文件包含malloc()等函数*/
typedef int DataType;/*定义DataType为int*/
typedef struct Node
{
DataType data;
struct Node *next;
} SLNode;
void ListInitiate(SLNode **head)/*初始化*/
{
/*如果有内存空间,申请头结点空间并使头指针head指向头结点*/
if ((*head = (SLNode *)malloc(sizeof(SLNode))) == NULL) exit(1);
(*head)->next = NULL;/*置链尾标记NULL */
}
int ListLength(SLNode *head) /* 单链表的长度*/
{
SLNode *p = head;/*p指向首元结点*/
int size = 0;/*size初始为0*/
while (p->next != NULL)/*循环计数*/
{
p = p->next;
size++;
}
return size;
}
int ListInsert(SLNode *head, int i, DataType x)
/*在带头结点的单链表head的数据元素ai(0 ≤ i ≤ size)结点前*/
/*插入一个存放数据元素x的结点*/
{
SLNode *p, *q;
int j;
p = head; /*p指向首元结点*/
j = -1;/*j初始为-1*/
while (p->next != NULL && j < i - 1)
/*最终让指针p指向数据元素ai-1结点*/
{
p = p->next;
j++;
}
if (j != i - 1)
{
printf("插入位置参数错!");
return 0;
}
/*生成新结点由指针q指示*/
if ((q = (SLNode *)malloc(sizeof(SLNode))) == NULL) exit(1);
q->data = x;
//此段程序有一处错误
q->next = p->next;/*给指针q->next赋值*/
p->next = q;/*给指针p->next重新赋值*/
return 1;
}
int ListDelete(SLNode *head, int i, DataType *x)
/*删除带头结点的单链表head的数据元素ai(0 ≤ i ≤ size - 1)结点*/
/*删除结点的数据元素域值由x带回。删除成功时返回1;失败返回0*/
{
SLNode *p, *s;
int j;
p = head; /*p指向首元结点*/
j = -1;/*j初始为-1*/
while (p->next != NULL && p->next->next != NULL && j < i - 1)
/*最终让指针p指向数据元素ai-1结点*/
{
p = p->next;
j++;
}
if (j != i - 1)
{
printf("删除位置参数错!");
return 0;
}
//此段程序有一处错误
s = p->next; /*指针s指向数据元素ai结点*/
*x = s->data;/*把指针s所指结点的数据元素域值赋予x*/
p->next = s->next;/*把数据元素ai结点从单链表中删除*/
free(s);/*释放指针s所指结点的内存空间*/
return 1;
}
int ListGet(SLNode *head, int i, DataType *x)
/*取数据元素ai和删除函数类同,只是不删除数据元素ai结点*/
{
SLNode *p;
int j;
p = head;
j = -1;
while (p->next != NULL && j < i)
{
p = p->next; j++;
}
if (j != i)
{
printf("取元素位置参数错!");
return 0;
}
//此段程序有一处错误
*x = p->data;
return 1;
}
void Destroy(SLNode **head)
{
SLNode *p, *p1;
p = *head;
while (p != NULL)
{
p1 = p;
p = p->next;
free(p1);
}
*head = NULL;
}
int main()
{
SLNode *head;
int i, x;
ListInitiate(&head);/*初始化*/
for (i = 0; i < 10; i++)
{
if (ListInsert(head, i, i + 1) == 0) /*插入10个数据元素*/
{
printf("错误! \n");
return 0;
}
}
if (ListDelete(head, 4, &x) == 0) /*删除数据元素5*/
{
printf("错误! \n");
return 0;
}
for (i = 0; i < ListLength(head); i++)
{
if (ListGet(head, i, &x) == 0) /*取元素*/
{
printf("错误! \n");
return 0;
}
else printf("%d ", x);/*显示数据元素*/
}
Destroy(&head);}
有序链表合并:
#include<stdio.h>
#include<malloc.h>
typedef struct node
{
int data;
struct node *next;
}LNode,*LinkList;
LinkList GreatLinkList(int n)
{
LinkList p, r, list = NULL;
int e;
int i;
for(i=1;i<=n;i++)
{
scanf("%d",&e);
p=(LinkList)malloc(sizeof(LNode));
p->data=e;
p->next=NULL;
if(list == NULL)
{
list = p;
}
else
{
r->next = p;
}
r = p;
}
return list;
}
LinkList MergeList(LinkList list1,LinkList list2)
{
LinkList list3;
LinkList p = list1,q = list2;
LinkList r;
if(list1->data <= list2->data)
{
list3 = list1;
r = list1;
p = list1->next;
}
else
{
list3 = list2;
r = list2;
q = list2 ->next;
}
while(p!=NULL && q!=NULL)
{
if(p->data<=q->data)
{
r->next = p;
r = p;
p = p->next;
}
else
{
r->next = q;
r = q;
q = q->next;
}
}
r->next = p?p:q;
return list3;
}
void printLink(LinkList list)
{
while (list != NULL)
{
printf("%3d",list->data);
list = list->next;
}
printf("\n");
}
main()
{
LinkList list1,list2,list3;
printf("输入表A的十个元素\n");
list1 = GreatLinkList(10);
printf("\n表A的元素为\n");
printLink(list1);
printf("\n输入表B的十个元素\n");
list2 = GreatLinkList(10);
printf("\n表B的元素为\n");
printLink(list2);
printf("\n");
list3 = MergeList(list1,list2);
printf("\n合并后表C的元素为\n");
printLink(list3);
printf("\n");
getchar();
getchar();
}
五、实验实习结果分析和(或)源程序调试过程
改错:
实验三:栈的实现及应用
一、实验实习目的及要求
实验目的:1.掌握栈的存储表示和实现
2.掌握栈的基本操作实现。
3.掌握栈在解决实际问题中的应用。
实验要求:设计一个程序,演示用算符优先法对算术表达式求值的过程。利用算符优先关系,实现对算术四则混合运算表达式的求值。
(1)输入的形式:表达式,例如2*(3+4)#
包含的运算符只能有'+' 、'-' 、'*' 、'/' 、'('、 ')',“#”代表输入结束符;
(2)输出的形式:运算结果,例如2*(3+4)=14;
(3)程序所能达到的功能:对表达式求值并输出。
二、实验实习设备(环境)及要求(软硬件条件)
实验室B515,电脑。
三、实验实习项目、内容与步骤
实验项目:栈的实现及应用
实验内容:掌握栈的结构,将栈应用于表达式计算问题
实验步骤:为了实现用栈计算算数表达式的值,需设置两个工作栈:用于存储运算符的栈opter,以及用于存储操作数及中间结果的栈opnd。
算法基本思想如下:
(1)首先将操作数栈opnd设为空栈,而将'#'作为运算符栈opter的栈底元素,这样的目的是判断表达式是否求值完毕。
(2)依次读入表达式的每个字,表达式须以'#'结,读入字符若是操作数则入栈opnd,读入字符若是运算符,则将此运算符c与opter的栈顶元素top比较优先级后执行相应的操作,具体操作如下:
(i)若top的优先级小于c,即top<c,则将c直接入栈opter,并读入下一字符赋值给c;
(ii)若top的优先级等于c,即top=c,则弹出opter的栈顶元素,并读入下一字符赋值给c,这一步目的是进行括号操作;
(iii)若top优先级高于c,即top>c,则表明可以计算,此时弹出opnd的栈顶两个元素,并且弹出opter栈顶的的运算符,计算后将结果放入栈opnd中。直至opter的栈顶元素和当前读入的字符均为'#',此时求值结束。
四、实验实习所得结果及分析
#include <stdio.h>
#include <stdlib.h>
#define MAXSIZE 20
//操作数
typedef struct Operand
{
int Data[MAXSIZE];
int top;
}Rand;
//运算符
typedef struct Operator
{
char Data[MAXSIZE];
int top;
}Rator;
//定义栈存放操作数和运算符
Rand operands;
Rator operators;
//初始化栈
void InitOperand(Rand *ra)
{
ra->top = -1;
}
void InitOperator(Rator *op)
{
op->top = -1;
}
//栈栈空
int EmptyRand(Rand *ra)
{
ra->top = -1;
return 0;
}
int EmptyRator(Rator *op)
{
op->top = -1;
return 0;
}
//进栈
int PushRand(Rand *ra,int e)
{
if(ra->top == MAXSIZE-1)
return 0;
ra->top++;
ra->Data[ra->top] = e;
return 1;
}
int PushRator(Rator *op,char e)
{
if(op->top == MAXSIZE-1)
return 0;
op->top++;
op->Data[op->top] = e;
return 1;
}
//出栈
int PopRand(Rand *ra,int *e)
{
if(ra->top == -1)
return 0;
*e = ra->Data[ra->top];
ra->top--;
return 1;
}
int PopRator(Rator *op,char *e)
{
if(op->top == -1)
return 0;
*e = op->Data[op->top];
op->top--;
return 1;
}
//取栈顶元素
int GetTopRand(Rand *ra)
{
if(ra->top == -1)
return 0;
return ra->Data[ra->top];
}
char GetTopRator(Rator *op)
{
if(op->top == -1)
return 'N';
return op->Data[op->top];//
}
//判断字符是否为运算符
int InOp(char ch)
{
if(ch == '(' || ch == ')' || ch == '+' || ch == '-' || ch == '*' || ch == '/' || ch == '#')
return 1;
return 0;
}
//判断运算符优先级
int Priority(char s)
{
switch(s)
{
case '(':
return 4;
case '*':
case '/':
return 3;
case '+':
case '-':
return 2;
case ')':
return 1;
default:
return 0;
}
}
//比较运算符优先级
int Precede(char op1,char op2)
{
if(Priority(op1) < Priority(op2))
return 0;
return 1;
}
//判断符号并运算
int Calculation(int a,int b,char c)
{
switch(c)
{
case '+':
return a+b;
case '-':
return a-b;
case '*':
return a*b;
case '/':
if(b == 0)
exit(1);
return a/b;
}
}
//计算表达式
int ExpCalculation(Rand *ra,Rator *op)
{
int a,b;
char ch,s;
PushRator(op,'#');
printf("请输入要计算的算式(以#结尾):\n");
ch = getchar();
while(ch != '#' || GetTopRator(op) != '#')
{
if(!InOp(ch))
{
int temp;
temp = ch - '0';
ch = getchar();
while(!InOp(ch))
{
temp = temp * 10 + ch - '0';
ch = getchar();
}
PushRand(ra,temp);
}
else
{
if(GetTopRator(op) == '(')
{
if(ch == ')')
PopRator(op,&s);
else
PushRator(op,ch);
ch = getchar();
}
else
{
if(!Precede(GetTopRator(op),ch))
{
PushRator(op,ch);
ch = getchar();
}
else
{
PopRand(ra,&b);
PopRand(ra,&a);
PopRator(op,&s);
PushRand(ra,Calculation(a,b,s));
}
}
}
}
printf("运算结果为%d\n",GetTopRand(ra));
return 0;
}
int main()
{
InitOperand(&operands);
InitOperator(&operators);
while(1)
{
char ch;
ExpCalculation(&operands,&operators);
EmptyRand(&operands);
EmptyRator(&operators);
ch = getchar();
if(ch==' ')//空格结束
{
exit(0);
}
}
return 0;
}
五、实验实习结果分析和(或)源程序调试过程
四则运算:
实验四:队列的实现及应用
一、实验实习目的及要求
实验目的:
1.掌握队列的存储表示和实现。
2.掌握队列的基本操作实现。
3.掌握队列在解决实际问题中的应用。
实验要求:
利用队列模拟服务台前的排队现象问题。
问题描述:某银行有一个客户办理业务站,在单位时间内随机地有客户到达,设每位客户的业务办理时间是某个范围的随机值。设只有一个窗口,一位业务人员,要求程序模拟统计在设定时间内,业务人员的总空闲时间和客户的平均等待时间。假定模拟数据已按客户到达的先后顺序依次存于某个正文数据文件中,对应每位客户有两个数据:到达时间和需要办理业务的时间,文本文件内容如:10 20 23 10 45 5 55 10 58 15 65 10。
二、实验实习设备(环境)及要求(软硬件条件)
实验室B515,电脑。
三、实验实习项目、内容与步骤
实验项目:队列的实现及应用
实验内容:掌握队列的结构,将队列应用于模拟服务台前的排队现象问题
实验步骤:与栈相对应,队列是一种先进先出的线性表。它只允许在表的一端进行插入,而在另一端进行删除元素。允许插入的一端称队尾,允许删除的一端称队头。插入与删除分别称为入队与出队,编写程序。
四、实验实习所得结果及分析
程序:
#include<stdio.h>
#include<stdlib.h>
typedef struct
{
int arrive;
int treat;
}QNODE;
typedef struct node
{
QNODE data;
struct node*next;
}LNODE;
LNODE *front,*rear;
void inQueue(QNODE e)
{
LNODE *p=(LNODE*)malloc(sizeof(LNODE*));
p->data=e;
p->next=NULL;
if(!front)
front=rear=p;
else
rear=rear->next=p;
}
int outQueue(QNODE *e)
{
LNODE*delp;
if(!front)
return 0;
*e=front->data;
delp=front;
front =front->next;
if(!front)
{
rear=NULL;}
free(delp);
return 1;
}
int main()
{
char Fname[120];
FILE *fp;
QNODE temp,curr;
int have=0,dwait=0,clock=0,wait=0,count=0,finish;
printf("输入文件名称:\n");
scanf("%s",Fname);
if((fp=fopen(Fname,"r"))==NULL)
printf("文件打开出错");
front=rear=NULL;
have=fscanf(fp,"%d" "%d",&temp.arrive ,&temp.treat );
do
{
if(!front&&!(have-2))
{
dwait+=temp.arrive -clock;
clock=temp.arrive ;
inQueue(temp);
have=fscanf(fp,"%d" "%d",&temp.arrive ,&temp.treat );
}
count++;
outQueue(&curr);
wait+=(clock-curr.arrive );
finish=clock+curr.treat ;
while(!(have-2)&&temp.arrive <=finish)
{
inQueue(temp);
have=fscanf(fp,"%d" "%d",&temp.arrive ,&temp.treat );
}
clock=finish;
}while(!(have-2)||front);
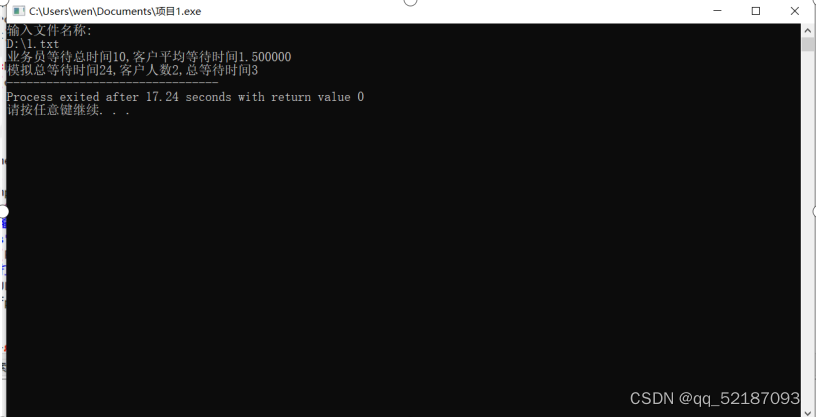
printf("业务员等待总时间%d,客户平均等待时间%f\n",dwait,(double)wait/count);
printf("模拟总等待时间%d,客户人数%d,总等待时间%d",clock,count,wait);
return 0;
}
五、实验实习结果分析和(或)源程序调试过程
文档:
实验五:二叉树操作及应用
- 实验实习目的及要求
实验目的:
掌握二叉树的定义、结构特征,以及各种存储结构的特点及使用范围,各种遍历算法。掌握用指针类型描述、访问和处理二叉树的运算。掌握前序或中序的非递归遍历算法。
实验要求:
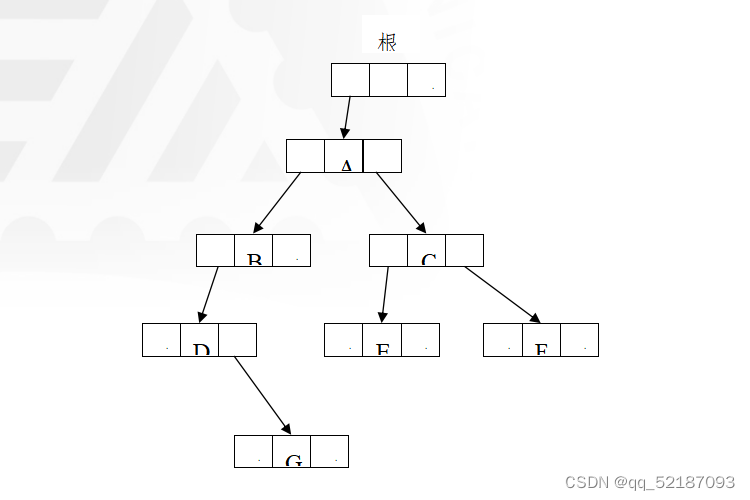
有如下二叉树:
程序代码给出了该二叉树的链式存储结构的建立、前序、中序、后序遍历的算法,同时也给出了查询“E”是否在二叉树里的代码。代码有三处错误,有标识,属于逻辑错误,对照书中的代码仔细分析后,请修改了在电脑里运行。
二、实验实习设备(环境)及要求(软硬件条件)
实验室B515,电脑。
三、实验实习项目、内容与步骤
1.改正程序错误。
2.编写二叉树的前序(或中序)的非递归遍历算法并进行测试。
四、实验实习所得结果及分析
改错:
#include<stdio.h>
#include<stdlib.h>
typedef char DataType;
typedef struct Node
{
DataType data;/*数据域*/
struct Node *leftChild;/*左子树指针*/
struct Node *rightChild;/*右子树指针*/
}BiTreeNode;/*结点的结构体定义*/
/*初始化创建二叉树的头结点*/
void Initiate(BiTreeNode **root)
{
*root = (BiTreeNode *)malloc(sizeof(BiTreeNode));
(*root)->leftChild = NULL;
(*root)->rightChild = NULL;
}
void Destroy(BiTreeNode **root)
{
if((*root) != NULL && (*root)->leftChild != NULL)
Destroy(&(*root)->leftChild);
if((*root) != NULL && (*root)->rightChild != NULL)
Destroy(&(*root)->rightChild);
free(*root);
}
/*若当前结点curr非空,在curr的左子树插入元素值为x的新结点*/
/*原curr所指结点的左子树成为新插入结点的左子树*/
/*若插入成功返回新插入结点的指针,否则返回空指针*/
BiTreeNode *InsertLeftNode(BiTreeNode *curr, DataType x)
{
BiTreeNode *s, *t;
if(curr == NULL) return NULL;
t = curr->leftChild;/*保存原curr所指结点的左子树指针*/
s = (BiTreeNode *)malloc(sizeof(BiTreeNode));
s->data = x;
s->leftChild = t;/*新插入结点的左子树为原curr的左子树*/
s->rightChild = NULL;
curr->leftChild = s;/*新结点成为curr的左子树*/
return curr->leftChild;/*返回新插入结点的指针*/
}
/*若当前结点curr非空,在curr的右子树插入元素值为x的新结点*/
/*原curr所指结点的右子树成为新插入结点的右子树*/
/*若插入成功返回新插入结点的指针,否则返回空指针*/
BiTreeNode *InsertRightNode(BiTreeNode *curr, DataType x)
{
BiTreeNode *s, *t;
if(curr == NULL) return NULL;
t = curr->rightChild;/*保存原curr所指结点的右子树指针*/
s = (BiTreeNode *)malloc(sizeof(BiTreeNode));
s->data = x;
s->rightChild = t;/*新插入结点的右子树为原curr的右子树*/
s->leftChild = NULL;
curr->rightChild = s;/*新结点成为curr的右子树*/
return curr->rightChild;/*返回新插入结点的指针*/
}
void PreOrder(BiTreeNode *t, void visit(DataType item))
//使用visit(item)函数前序遍历二叉树t
{
if(t != NULL)
{//此小段有一处错误
visit(t->data);
PreOrder(t-> leftChild, visit);
PreOrder(t-> rightChild, visit);
}
}
void InOrder(BiTreeNode *t, void visit(DataType item))
//使用visit(item)函数中序遍历二叉树t
{
if(t != NULL)
{//此小段有一处错误
InOrder(t->leftChild, visit);
visit(t->data);
InOrder(t->rightChild, visit);
}
}
void PostOrder(BiTreeNode *t, void visit(DataType item))
//使用visit(item)函数后序遍历二叉树t
{
if(t != NULL)
{//此小段有一处错误
PostOrder(t->leftChild, visit);
PostOrder(t->rightChild, visit);
visit(t->data);
}
}
void visit(DataType item)
{
printf("%c ", item);
}
BiTreeNode *Search(BiTreeNode *root, DataType x)//需找元素x是否在二叉树中
{
BiTreeNode *find=NULL;
if(root!=NULL)
{
if(root->data==x)
find=root;
else
{
find=Search(root->leftChild,x);
if(find==NULL)
find=Search(root->rightChild,x);
}
}
return find;
}
int main()
{
BiTreeNode *root, *p, *pp,*find;
char x='E';
Initiate(&root);
p = InsertLeftNode(root, 'A');
p = InsertLeftNode(p, 'B');
p = InsertLeftNode(p, 'D');
p = InsertRightNode(p, 'G');
p = InsertRightNode(root->leftChild, 'C');
pp = p;
InsertLeftNode(p, 'E');
InsertRightNode(pp, 'F');
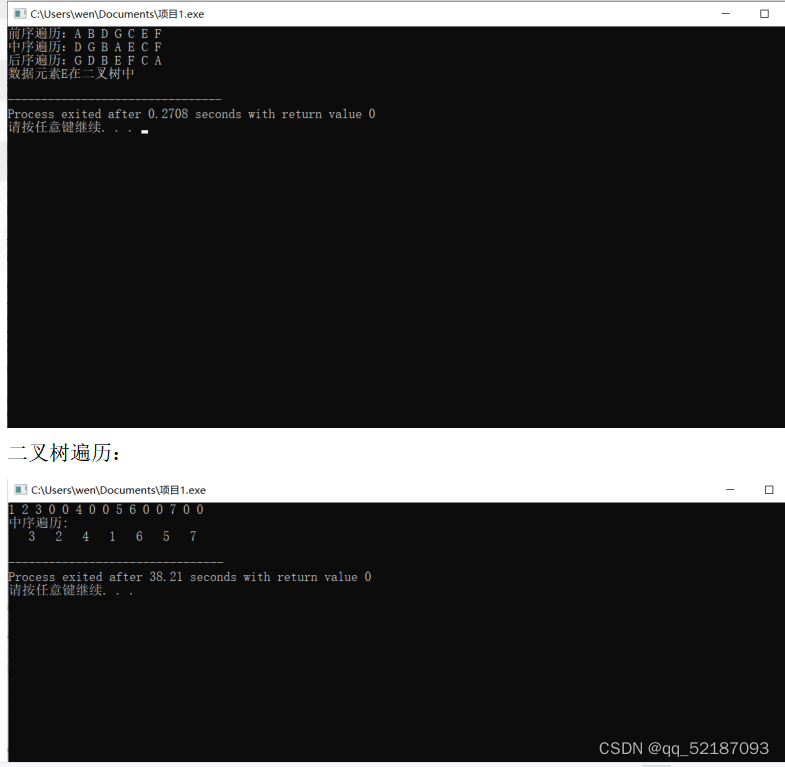
printf("前序遍历:");
PreOrder(root->leftChild, visit);
printf("\n中序遍历:");
InOrder(root->leftChild, visit);
printf("\n后序遍历:");
PostOrder(root->leftChild, visit);
find=Search(root,x);
if(find!=NULL)
printf("\n数据元素%c在二叉树中 \n",x);
else
printf("\n数据元素%c不在二叉树中 \n",x);
Destroy(&root);
}
二叉树中序遍历非递归:
#include <stdio.h>
#include <stdlib.h>
#define NULL 0
#define M 100
typedef struct node
{
int data;
int cishu;
struct node *lchild;
struct node *rchild;
}bitree;
typedef struct stack
{
bitree *elements[M];
int top;
}seqstack;
bitree *root;
seqstack s;
void setnull()
{
s.top =0;
}
void push(bitree *temp)
{
s.elements[s.top++] = temp;
}
bitree *pop()//取栈顶并出栈顶
{
return s.elements[--s.top];
}
int empty()
{
return s.top == 0;
}
bitree *creat()
{ bitree *t;
int x;
scanf("%d",&x);
if(x==0) t=NULL;
else{
t=(bitree*)malloc(sizeof(bitree));
t->data=x;
t->lchild=creat();
t->rchild=creat();
}
return t;
}
void inorder(bitree *t)//中序遍历的非递归算法
{
bitree *temp = t;
while(temp != NULL||s.top != 0)
{
while(temp != NULL)
{
push(temp);
temp = temp->lchild;
}
if(s.top != 0)
{
temp = pop();
printf("%4d",temp->data);
temp = temp->rchild;
}
}
printf("\n");
}
int main()
{
bitree *root;
setnull();
root=creat();
printf("中序遍历:\n");
inorder(root);
return 0;
}
五、实验实习结果分析和(或)源程序调试过程
实验六、图的遍历操作及应用
一、实验实习目的及要求
实验目的:掌握有向图和无向图的概念;掌握邻接矩阵和邻接链表建立图的存储结构;掌握DFS及BFS对图的遍历操作;了解图结构在人工智能、工程等领域的广泛应用。
实验要求:采用邻接矩阵和邻接链表作为图的存储结构,完成有向图和无向图的DFS和BFS操作。本实验给出了示例程序,其中共有4处错误,错误段均有标识,属于逻辑错误。请认真理解程序,修改程序代码,并在电脑上调试运行。
二、实验实习设备(环境)及要求(软硬件条件)
实验室B515,电脑。
三、实验实习项目、内容与步骤
实验项目:图的遍历操作及应用
实验内容:实现图的存储、深度遍历和广度遍历算法
实验步骤:深度优先搜索法DFS的基本思想:从图G中某个顶点Vo出发,首先访问Vo,然后选择一个与Vo相邻且没被访问过的顶点Vi访问,再从Vi出发选择一个与Vi相邻且没被访问过的顶点Vj访问,……依次继续。如果当前被访问过的顶点的所有邻接顶点都已被访问,则回退到已被访问的顶点序列中最后一个拥有未被访问的相邻顶点的顶点W,从W出发按同样方法向前遍历。直到图中所有的顶点都被访问。
广度优先算法BFS的基本思想:从图G中某个顶点Vo出发,首先访问Vo,然后访问与Vo相邻的所有未被访问过的顶点V1,V2,……,Vt;再依次访问与V1,V2,……,Vt相邻的起且未被访问过的的所有顶点。如此继续,直到访问完图中的所有顶点。根据深度优先搜索法和广度优先搜索法改正程序中的错误。
四、实验实习所得结果及分析
改错1:
#include"stdio.h"
#include"stdlib.h"
#define MaxVertexNum 100 //定义最大顶点数
typedef struct{
char vexs[MaxVertexNum]; //顶点表
int edges[MaxVertexNum][MaxVertexNum];
//邻接矩阵,可看作边表
int n,e; //图中的顶点数n和边数e
}MGraph; //用邻接矩阵表示的图的类型
//=========建立邻接矩阵=======
void CreatMGraph(MGraph *G)
{
int i,j,k;
char a;
printf("Input VertexNum(n) and EdgesNum(e): ");
scanf("%d,%d",&G->n,&G->e); //输入顶点数和边数
scanf("%c",&a);
printf("Input Vertex string:");
for(i=0;i<G->n;i++)
{
scanf("%c",&a);
G->vexs[i]=a; //读入顶点信息,建立顶点表
}
for(i=0;i<G->n;i++)
for(j=0;j<G->n;j++)
G->edges[i][j]=0; //初始化邻接矩阵
printf("Input edges,Creat Adjacency Matrix\n");
for(k=0;k<G->e;k++) { //读入e条边,建立邻接矩阵
scanf("%d%d",&i,&j); //输入边(Vi,Vj)的顶点序号
G->edges[i][j]=1;
G->edges[j][i]=1; //若为无向图,矩阵为对称矩阵;若建立有向图,去掉该条语句
}
}
//=========定义标志向量,为全局变量=======
typedef enum{FALSE,TRUE} Boolean;
Boolean visited[MaxVertexNum];
//========DFS:深度优先遍历的递归算法======
void DFSM(MGraph *G,int i)
{ //以Vi为出发点对邻接矩阵表示的图G进行DFS搜索,邻接矩阵是0,1矩阵
int j;
printf("%c",G->vexs[i]); //访问顶点Vi
visited[i]=TRUE; //置已访问标志
for(j=0;j<G->n;j++) //依次搜索Vi的邻接点
if(G->edges[i][j]==1 && ! visited[j])
DFSM(G,j); //(Vi,Vj)∈E,且Vj未访问过,故Vj为新出发点
}
void DFS(MGraph *G)
{ //此段代码有一处错误
int i;
for(i=0;i<G->n;i++)
visited[i]=FALSE; //标志向量初始化
for(i=0;i<G->n;i++)
if(!visited[i]) //Vi未访问过
DFSM(G,i); //以Vi为源点开始DFS搜索
}
//===========BFS:广度优先遍历=======
void BFS(MGraph *G,int k)
{ //以Vk为源点对用邻接矩阵表示的图G进行广度优先搜索
int i,j,f=0,r=0;
int cq[MaxVertexNum]; //定义队列
for(i=0;i<G->n;i++)
visited[i]=FALSE; //标志向量初始化
for(i=0;i<=G->n;i++)
cq[i]=-1; //队列初始化
printf("%c",G->vexs[k]); //访问源点Vk
visited[k]=TRUE;
cq[r]=k; //Vk已访问,将其入队。注意,实际上是将其序号入队
while(cq[f]!=-1) { //队非空则执行
i=cq[f]; f=f+1; //Vf出队
for(j=0;j<G->n;j++) //依次Vi的邻接点Vj
if(G->edges[i][j]==1 && !visited[j]) { //Vj未访问 以下三行代码有一处错误
printf("%c",G->vexs[j]); //访问Vj
visited[j]=TRUE; r=r+1; cq[r]=j; //访问过Vj入队
}
}
}
//==========main=====
int main()
{
MGraph *G;
G=(MGraph *)malloc(sizeof(MGraph)); //为图G申请内存空间
CreatMGraph(G); //建立邻接矩阵
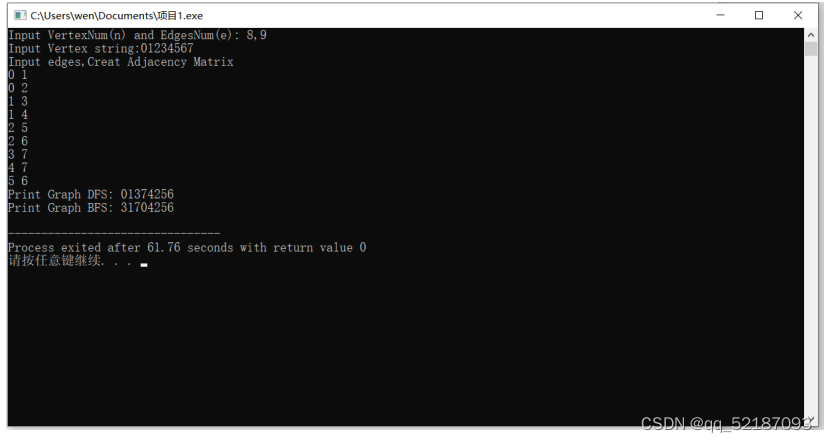
printf("Print Graph DFS: ");
DFS(G); //深度优先遍历
printf("\n");
printf("Print Graph BFS: ");
BFS(G,3); //以序号为3的顶点开始广度优先遍历
printf("\n");}
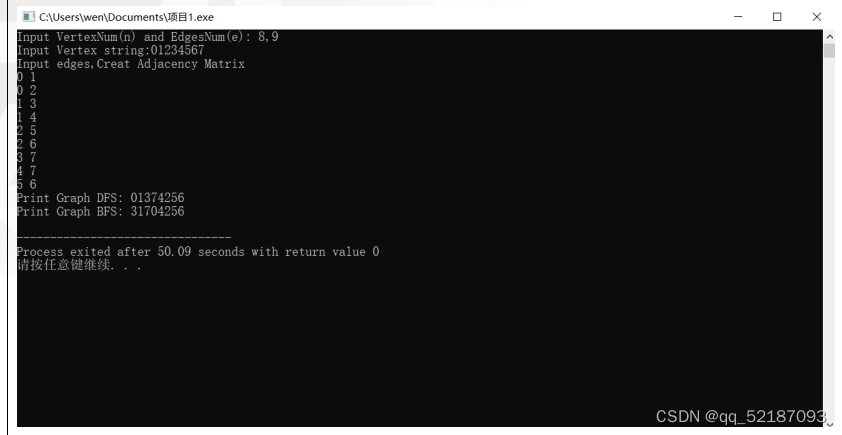
改错2:
五、实验实习结果分析和(或)源程序调试过程
改错1:
改错2:
#include"stdio.h"
#include"stdlib.h"
#define MaxVertexNum 50 //定义最大顶点数
typedef struct node{ //边表结点
int adjvex; //邻接点域
struct node *next; //链域
}EdgeNode;
typedef struct vnode{ //顶点表结点
char vertex; //顶点域
EdgeNode *firstedge; //边表头指针
}VertexNode;
typedef VertexNode AdjList[MaxVertexNum]; //AdjList是邻接表类型
typedef struct {
AdjList adjlist; //邻接表
int n,e; //图中当前顶点数和边数
} ALGraph; //图类型
//=========建立图的邻接表=======
void CreatALGraph(ALGraph *G)
{
int i,j,k;
char a;
EdgeNode *s; //定义边表结点
printf("Input VertexNum(n) and EdgesNum(e): ");
scanf("%d,%d",&G->n,&G->e); //读入顶点数和边数
scanf("%c",&a);
printf("Input Vertex string:");
for(i=0;i<G->n;i++) //建立顶点表
{
scanf("%c",&a);
G->adjlist[i].vertex=a; //读入顶点信息
G->adjlist[i].firstedge=NULL; //边表置为空表
}
printf("Input edges,Creat Adjacency List\n");
for(k=0;k<G->e;k++) { //建立边表
scanf("%d%d",&i,&j); //读入边(Vi,Vj)的顶点对序号
s=(EdgeNode *)malloc(sizeof(EdgeNode)); //生成边表结点
s->adjvex=j; //邻接点序号为j
s->next=G->adjlist[i].firstedge;
G->adjlist[i].firstedge=s; //将新结点*S插入顶点Vi的边表头部
s=(EdgeNode *)malloc(sizeof(EdgeNode));
s->adjvex=i; //邻接点序号为i
s->next=G->adjlist[j].firstedge;
G->adjlist[j].firstedge=s; //将新结点*S插入顶点Vj的边表头部
}
}
//=========定义标志向量,为全局变量=======
typedef enum{FALSE,TRUE} Boolean;
Boolean visited[MaxVertexNum];
//========DFS:深度优先遍历的递归算法======
void DFSM(ALGraph *G,int i)
{ //以Vi为出发点对邻接链表表示的图G进行DFS搜索
EdgeNode *p;
printf("%c",G->adjlist[i].vertex); //访问顶点Vi
visited[i]=TRUE; //标记Vi已访问
p=G->adjlist[i].firstedge; //取Vi边表的头指针
while(p) { //依次搜索Vi的邻接点Vj,这里j=p->adjvex
//以下3行代码有一处错误
if(! visited[p->adjvex]) //若Vj尚未被访问
DFSM(G,p->adjvex); //则以Vj为出发点向纵深搜索
p=p->next; //找Vi的下一个邻接点
}
}
void DFS(ALGraph *G)
{
int i;
for(i=0;i<G->n;i++)
visited[i]=FALSE; //标志向量初始化
for(i=0;i<G->n;i++)
if(!visited[i]) //Vi未访问过
DFSM(G,i); //以Vi为源点开始DFS搜索
}
//==========BFS:广度优先遍历=========
void BFS(ALGraph *G,int k)
{ //以Vk为源点对用邻接链表表示的图G进行广度优先搜索
int i,f=0,r=0;
EdgeNode *p;
int cq[MaxVertexNum]; //定义FIFO队列
for(i=0;i<G->n;i++)
visited[i]=FALSE; //标志向量初始化
for(i=0;i<=G->n;i++)
cq[i]=-1; //初始化标志向量
printf("%c",G->adjlist[k].vertex); //访问源点Vk
visited[k]=TRUE;
cq[r]=k; //Vk已访问,将其入队。注意,实际上是将其序号入队
while(cq[f]!=-1)
{ //队列非空则执行
i=cq[f]; f=f+1; //Vi出队
p=G->adjlist[i].firstedge; //取Vi的边表头指针
while(p)
{ //依次搜索Vi的邻接点Vj(令p->adjvex=j)
if(!visited[p->adjvex]) { //若Vj未访问过
printf("%c",G->adjlist[p->adjvex].vertex); //访问Vj
visited[p->adjvex]=TRUE;
//以下3行代码有一处错误
r=r+1; cq[r]=p->adjvex; //访问过的Vj入队
}
p=p->next; //找Vi的下一个邻接点
}
}//endwhile
}
//==========主函数===========
void main()
{
int i;
ALGraph *G;
G=(ALGraph *)malloc(sizeof(ALGraph));
CreatALGraph(G);
printf("Print Graph DFS: ");
DFS(G);
printf("\n");
printf("Print Graph BFS: ");
BFS(G,3);
printf("\n");
}
实验七、查找算法的实现
一、实验实习目的及要求
实验目的:掌握顺序和二分查找算法的基本思想及其实现方法。
实验要求:问题描述:对给定的任意数组(设其长度为n),分别用顺序和二分查找方法在此数组中查找与给定值k相等的元素。
二、实验实习设备(环境)及要求(软硬件条件)
实验室B515,电脑。
三、实验实习项目、内容与步骤
实验项目:查找算法的实现
实验内容:实现顺序表的二分查找算法
实验步骤:顺序查找基本思想:从查找表的一端开始,逐个将记录的关键字值和给定值进行比较,如果某个记录的关键字值和给定值相等,则称查找成功;否则,说明查找表中不存在关键字值为给定值的记录,则称查找失败。
二分查找基本思想:先取查找表的中间位置的关键字值与给定关键字值作比较,若它们的值相等,则查找成功;如果给定值比该记录的关键字值大,说明要查找的记录一定在查找表的后半部分,则在查找表的后半部分继续使用折半查找;若给定值比该记录的关键字值小,说明要查找的记录一定在查找表的前半部分,则在查找表的前半部分继续使用折半查找。…直到查找成功,或者直到确定查找表中没有待查找的记录为止,即查找失败。
写出两种查找方式的代码。
四、实验实习所得结果及分析
顺序查找:
#include<stdio.h>
#include<stdlib.h>
int Seqsearch(int R[],int n,int k)
{
int i=0;
while(i<n&&R[i]!=k)
{
printf("%d ",R[i]);
i++;
}
if(i>=n)
return -1;
else{
printf("%d",R[i]);
return i;
}
}
int main()
{
int a[10]={9,13,15,7,4,3,5,8,6,36};
int k,loc;
printf("输入要查找的数");
scanf("%d",&k);
loc=Seqsearch(a,10,k);
printf("\n");
printf("该数的位置是:%d\n",loc);
return 0;
}
折半查找:
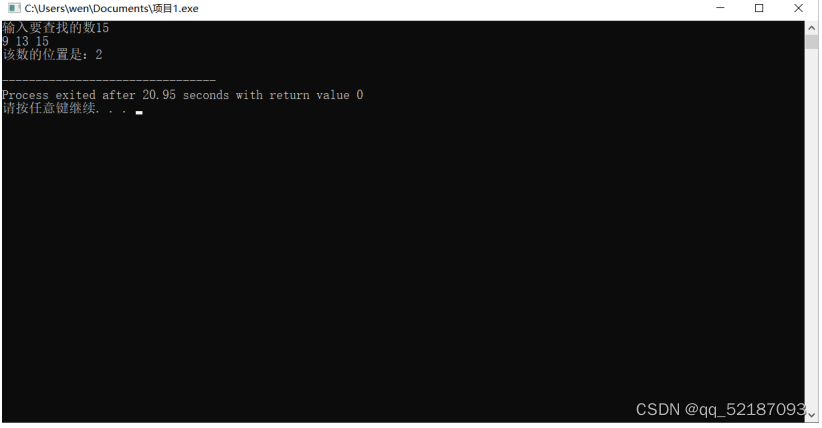
五、实验实习结果分析和(或)源程序调试过程
实验任务:
顺序查找:
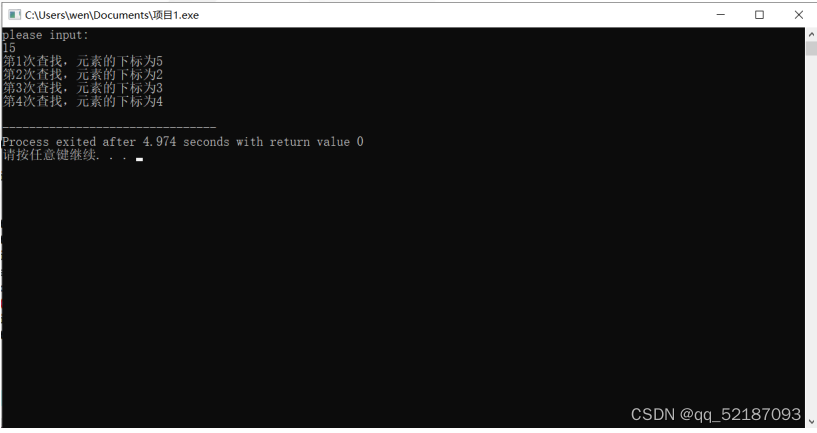
折半查找:
#include<stdio.h>
#include<stdlib.h>
int BinSearch(int R[],int n,int k)
{
int low=0,high=n-1,mid,count=0;
while(low<=high)
{
mid=(low+high)/2;
printf("第%d次查找,元素的下标为%d\n",++count,mid);
if(R[mid]==k)
return mid;
if(R[mid]>k)
high=mid-1;
else
low=mid+1;
}
return -1;
}
int main()
{
int a[11]={5,7,9,12,15,18,20,22,25,30,100};
int k,loc;
printf("please input:\n");
scanf("%d",&k);
loc=BinSearch(a,11,k);
if(loc==-1)
printf("未查询到");
return 0;
}
实验八、排序算法的实现
一、实验实习目的及要求
实验目的:
1. 掌握常用的排序方法,并掌握用高级语言实现排序算法的方法;
2. 深刻理解排序的定义和各种排序方法的特点,并能加以灵活应用;
3. 了解各种方法的排序过程及其时间复杂度的分析方法。
实验要求:
统计成绩:给出n个学生的考试成绩表,每条信息由姓名和分数组成,试设计一个算法:
(1) 按分数高低次序,打印出每个学生在考试中获得的名次,分数相同的为同一名次;
(2) 按名次列出每个学生的姓名与分数。
二、实验实习设备(环境)及要求(软硬件条件)
实验室B515,电脑。
三、实验实习项目、内容与步骤
实验项目:排序算法的实现
实验内容:实现直接插入排序、快速排序等算法
实验步骤:
1.定义结构体。
Typedef struct student
{ char name[8];
int score; }
2.定义结构体数组。
3.编写主程序,对数据进行排序。
4.要求至少采用两种排序算法实现,如直接插入排序、快速排序等算法。
四、实验实习所得结果及分析
#include<stdio.h>
#include<stdlib.h>
typedef struct
{
char name[10];
int score;
} student;
void InsertSort(student a[],int n)
{
int i,j,flag;
student temp;
for(i=0; i<n-1; i++)
{
flag=0;
for(j=0; j<n-i-1; j++)
{
if(a[j].score<a[j+1].score)
{
temp=a[j];
a[j]=a[j+1];
a[j+1]=temp;
flag=1;
}
}
if(flag==0) break;
}
}
void SelectionSort(student a[],int n)
{
int i,j,k;
student temp;
for(i=0; i<n; i++)
{
k=i;
for(j=i; j<n; j++)
{
if(a[j].score>a[k].score) k=j;
}
if(k!=i)
{
temp=a[i];
a[i]=a[k];
a[k]=temp;
}
}
}
int main()
{
int n,i,k,t;
student *a;
printf("请输入学生的数量\n");
scanf("%d",&n);
a=(student *)malloc(n*sizeof(student));
printf("输入学生姓名和成绩:\n");
for(i=0; i<n; i++)
{
scanf("%s %d",&a[i].name,&a[i].score);
}
printf("选择排序方式(1)使用冒泡排序,(2)使用简单选择排序\n");
scanf("%d",&k);
if(k==1)
{
InsertSort(a,n);
}
else if(k==2)
{
SelectionSort(a,n);
}
printf("第%d名: %s %d\n",1,a[0].name,a[0].score);
t=1;
for(i=1; i<n; i++)
{
if(a[i].score==a[i-1].score)
{
printf("第%d名:%s %d\n",t,a[i].name,a[i].score);
}
else
{
t=i+1;
printf("第%d名: %s %d\n",t,a[i].name,a[i].score);
}
}
free(a);
return 0;
}
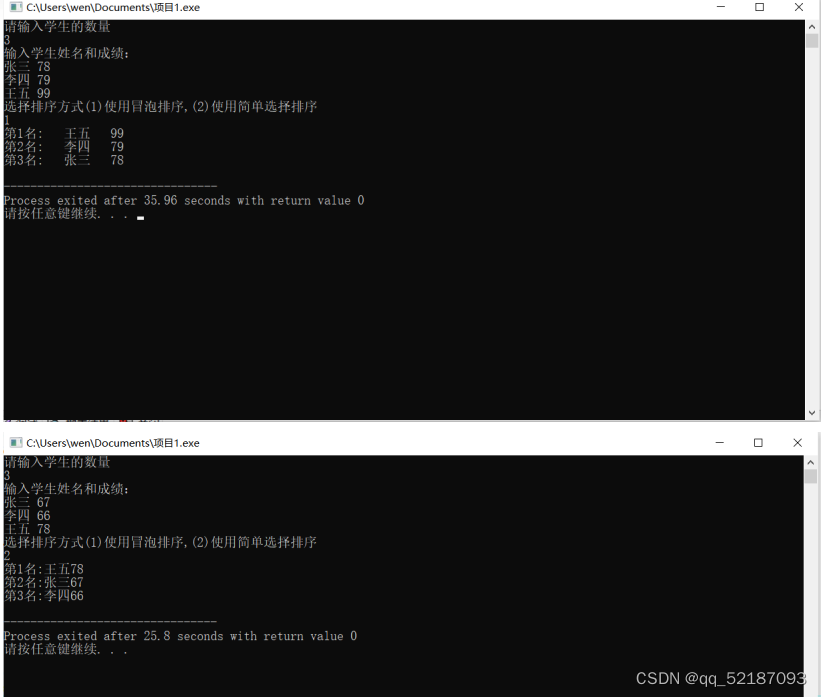
五、实验实习结果分析和(或)源程序调试过程