中等

在给定的 m x n 网格 grid 中，每个单元格可以有以下三个值之一：

• 值 0 代表空单元格；
• 值 1 代表新鲜橘子；
• 值 2 代表腐烂的橘子。

每分钟，腐烂的橘子 周围 4 个方向上相邻 的新鲜橘子都会腐烂。

返回 直到单元格中没有新鲜橘子为止所必须经过的最小分钟数。如果不可能，返回 -1 。

示例 1：

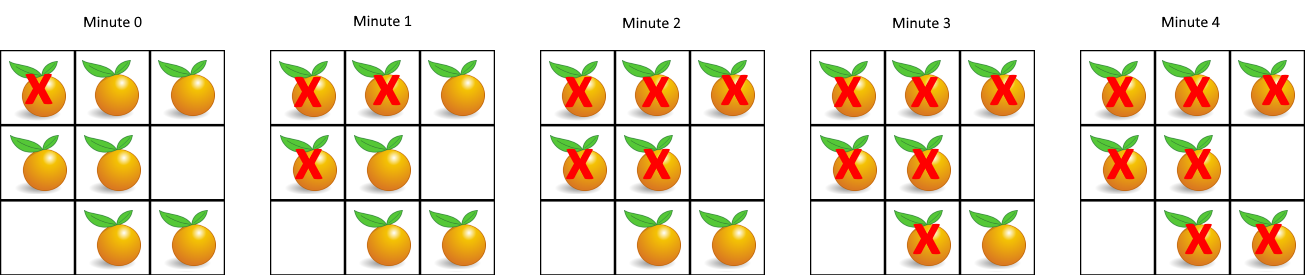
输入：grid = [[2,1,1],[1,1,0],[0,1,1]]
输出：4

示例 2：

输入：grid = [[2,1,1],[0,1,1],[1,0,1]]
输出：-1
解释：左下角的橘子（第 2 行， 第 0 列）永远不会腐烂，因为腐烂只会发生在 4 个方向上。

示例 3：

输入：grid = [[0,2]]
输出：0
解释：因为 0 分钟时已经没有新鲜橘子了，所以答案就是 0 。

提示：

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 10
• grid[i][j] 仅为 0、1 或 2

思路：使用time记录当前的分钟数

由于在找到腐烂水果后直接将它周围的水果置为腐烂水果，但是可能当前轮次腐烂的水果，又在当前轮次中影响周围水果，导致错误，所以可以标记：在不同轮次中被传染腐烂的水果标记为不同的数字，由于一开始time=0时，腐烂水果标记为2，所以在time=0到1这段时间被传染的水果标记为2+time+1,这样就可以使得本轮time=0时不会让标记为3的水果传染它周围的水果

class Solution {
    // 1：判断第i分钟第一次遇到未腐烂橘子，则time++表示还需要一分钟
    // 判断橘子完全腐烂时，将flag!=-1;
    // 当经过两轮剩余的未腐烂个数仍然相同说明不可能腐烂
    //逻辑错误，在找到腐烂水果后直接将它周围的水果置为腐烂水果，但是可能当前轮次腐烂的水果，又在当前轮次中影响周围水果，导致错误
    //解决，用不同数字标记，第0轮，为2，则下一轮依次+1
public:
bool in(vector<vector<int>>& grid,int i,int j){
    return i>=0&&i<grid.size()&&j>=0&&j<grid[0].size();
}
    int orangesRotting(vector<vector<int>>& grid) {
        int time = 0;

        int flag = -1;
        int good = 0;
        for (int i = 0; i < grid.size(); i++) {
            for (int j = 0; j < grid[0].size(); j++) {
                if (grid[i][j] == 1)
                    good++;
            }
        }      
        if (good == 0)
            return 0;
        while (good > 0) {
            int pre = good; // 该轮未进行前 新鲜的个数

            for (int i = 0; i < grid.size(); i++) {
                for (int j = 0; j < grid[0].size(); j++) {
                    if (grid[i][j] ==2+time) { // 有腐烂的橘子,对四周进行判断，有新鲜水果就腐烂
                        if (in(grid,i,j-1)&&grid[i][j - 1] == 1) {
                            grid[i][j - 1] = 2+time+1;
                            good--;
                        }
                        if (in(grid,i,j+1)&&grid[i][j + 1] == 1) {
                            grid[i][j + 1] = 2+time+1;
                             good--;
                        }
                        if (in(grid,i-1,j)&&grid[i - 1][j] == 1) {
                            grid[i - 1][j ] = 2+time+1;
                             good--;
                        }
                        if (in(grid,i+1,j)&&grid[i + 1][j] == 1) {
                             grid[i +1][j ] = 2+time+1;
                             good--;
                        }
                    }
                }
            }

            if (pre == good & good > 0)
                return -1; // 剩余的不可能腐烂
              time++;
            
        }
        return time;
    }
};