本文所涉及所有资源均在传知代码平台可获取

一、背景介绍

旅行商问题（Traveling Salesman Problem，TSP）是组合优化领域中的经典难题，在物流配送、电路布线、旅游规划等众多领域具有广泛应用。其目标是为旅行商找到一条遍历所有城市且不重复、最终回到起点的最短路径，随着城市数量的增加，问题的复杂性呈指数级增长，传统蚁群算法在求解TSP时存在易陷入局部最优解、收敛速度较慢、迭代次数多等问题。

量子计算的出现为解决复杂问题提供了新的思路和方法。量子蚁群算法（Quantum Ant Colony Optimization Algorithm，QACA）将量子理论与传统蚁群算法相结合，利用量子比特的特性增加信息编码的多样性，通过量子旋转门操作使当前解更靠近最优解，从而提高了算法的全局搜索能力和搜索效率。本复现旨在深入理解和验证量子蚁群算法在解决TSP问题上的有效性，为相关领域的路径优化问题提供更高效的解决方案。
原文链接

二、算法原理

（一）传统蚁群算法概述

1. 基本原理
   • 传统蚁群算法模拟自然界中蚂蚁的觅食行为，蚂蚁通过感知信息素浓度来选择路径，信息素浓度越高的路径被选择的概率越大，同时蚂蚁在走过的路径上留下信息素，形成正反馈机制，使整个蚁群逐渐收敛到最优路径。在TSP问题中，用蚂蚁的行走路径表示可行解，通过不断更新信息素浓度来寻找最短路径。
   • 其数学模型中，蚂蚁从城市(i)移动到城市(j)的概率(P_{ij}^k)与城市间距离(d_{ij})和信息素(\tau_{ij})有关，信息素更新法则考虑了信息素挥发和蚂蚁留下的信息素。

（二）量子蚁群算法改进策略

1. 量子比特与信息素编码
   

2. 信息素更新规则

   • 信息素更新包括挥发和增加两部分。首先，各路径上的信息素按(\tau_{ij}=(1-\rho)\tau_{ij})进行挥发，以避免信息素无限积累。然后，在有蚂蚁经过的路径上，信息素增加量(\Delta\tau_{ij})与量子态概率幅(\vert\beta_{ij}^k\vert2)、路径长度(L^k)以及量子信息素启发因子(\gamma)有关，当蚂蚁经过路径((i,j))时，该路径上的信息素概率幅(\beta_{ij})值会增大，信息素得到加强，反之则挥发。

3. 路径的矩阵表示与最优解选择

   • 对于(n)个城市的TSP问题，用矩阵(R^{k)表示第(k)只蚂蚁构建的路径，(R}k[i,j]=1)表示存在从城市(i)到(j)的路径。所有蚂蚁构建完路径后，根据路径长度排序选出当前最优解，其路径矩阵记为(R^{best})。

4. 量子旋转门操作
   

三、代码实现

（一）数据准备

1. 城市坐标生成
   • create_cities函数用于生成(n)个城市的随机坐标，坐标范围在(0)到(100)之间，模拟TSP问题中的城市分布情况。

（二）关键函数实现

1. 路径长度计算函数
   • calculate_distance函数计算给定路径的长度，通过计算路径中相邻城市间的欧几里得距离之和（考虑循环路径，最后一个城市与第一个城市相连），使用numpy的linalg.norm函数计算向量的范数来获取距离。
2. 信息素矩阵初始化函数
   • init_pheromone函数创建一个三维的信息素矩阵，初始值为(1)，用于存储蚂蚁在不同路径上留下的信息素浓度。
3. 信息素矩阵更新函数
   • update_pheromone函数根据信息素挥发率(\rho)和蚂蚁留下的信息素增量(\Delta\tau_{ij})更新信息素矩阵，使信息素浓度随时间变化，引导蚂蚁选择更优路径。
4. 量子旋转门函数
   • quantum_rotation_gate函数实现量子旋转门操作，根据给定的旋转角(\theta)对信息素概率幅(\alpha_{ij})和(\beta_{ij})进行旋转，更新信息素编码矩阵，使当前解向最优解靠近。
5. 量子蚁群算法主函数
   • quantum_ant_colony_optimization函数是算法的核心，执行以下操作：
     • 初始化参数，包括信息素矩阵、最优距离和路径等。
     • 进行迭代，在每次迭代中：
       • 所有蚂蚁构建路径，随机初始化路径并计算路径长度，更新最优解。
       • 更新信息素矩阵，计算蚂蚁在路径上留下的信息素增量。
       • 使用量子旋转门更新信息素矩阵，使信息素编码向最优解靠近。
       • 信息素挥发，根据挥发率更新信息素矩阵。
     • 迭代结束后，返回最优路径和最短距离。

（三）结果可视化

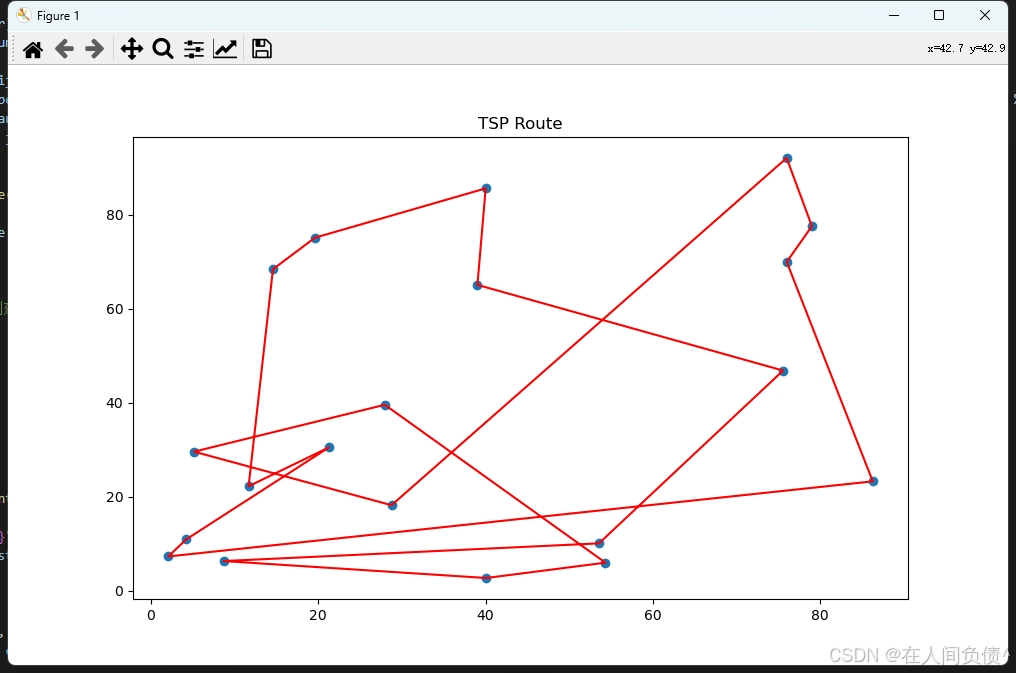
1. 路径绘制
   • 在主程序中，使用matplotlib库绘制城市坐标点和最优路径，将城市显示为散点，最优路径显示为红线，直观展示算法找到的最优路径。

四、实验结果

（一）实验设置

1. 参数调整
   • 在quantum_ant_colony_optimization函数中，可调整参数包括蚂蚁数量(N)、城市数量(n)、最大迭代次数(max_iter)、信息素挥发率(\rho)、信息素沉积常数(Q)、信息素重要度(\alpha)、启发式信息重要度(\beta)和量子信息素启发因子(\gamma)。增加蚂蚁数量和迭代次数可能提高解的质量，但会增加计算时间；调整(\rho)、(\alpha)、(\beta)和(\gamma)的值会影响信息素的更新和蚂蚁的路径选择策略，进而影响算法的收敛速度和搜索能力。

（二）结果展示

1. 最优路径和距离

   • 运行代码后，输出最优路径（Best route）和最佳距离（Best distance），展示算法在给定城市分布下找到的最优旅行商路径及其长度。通过多次运行代码或调整参数，可以进一步分析算法在不同条件下的性能表现，如最优解的稳定性、收敛速度等。与传统蚁群算法对比，可以验证量子蚁群算法在求解TSP问题上的有效性和优势，例如在收敛速度、搜索效率和避免陷入局部最优解方面的改进效果。

   • 

   • 

部署方式

• python 3.8以上

资源获取

详细复现过程的项目源码、数据和预训练好的模型可从该文章下方附件地址获取。

附件地址：量子蚁群算法复现