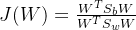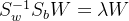一、LDA的基础介绍
LDA是一种有监督的降维方法,和它比较类似的是PCA(一种无监督的降维方法),如果对PCA不熟悉的朋友可以看看下面关于PCA的介绍。
1、PCA介绍和基本思想
主成分分析(PCA)是一种利用正交变换把由线性相关变量表示的观测数据转化为少数几个由线性无关变量表示的数据。
在主成分分析中,首先对给定的数据进行规范化,使得数据的每一变量的平均值为0,方差为1。之后对数据进行正交变换,原来由线性相关变量表示的数据,通过正交变换变成若干个线性无关的新变量表示的数据,新变量是可能的正交变换中变量的方差最大的,方差表示在新变量上信息的大小,将变量依次成为第一主成分,第二主成分。
2、PCA的相关定义
总体主成分分析的定义:
1 系数向量 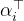
2 变量 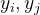
3 变量 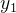
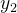
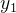
主成分分析的求法
假设 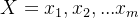
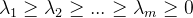
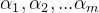
则𝑥的第𝑘主成分是:
则𝑥的第𝑘主成分的方差是:
其中𝑢=𝐸(𝑥),上式子为:
因此:
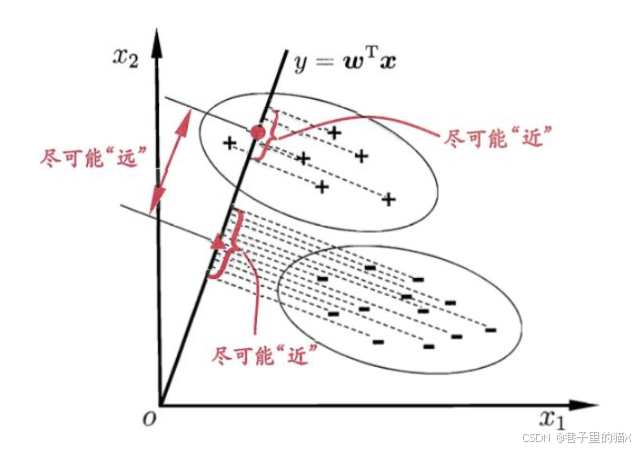
简单地介绍完PCA之后我们回到LDA地介绍。LDA与PCA相似的地方在于都是降维方法,参考的都是方差。不同的是LDA是有监督的,LDA的降维是:在投影之后,同类别的数据内方差尽可能小,不同类别之间的方差尽可能大。如果是将所有样本的X(特征)投影在同一条直线的话,那么就是label相同的数据投影结果应该很接近,反之label不一样的数据投影结果应该远一点。说起来很抽象,我们可以看一下下图:
"+"和"-"是两种label的类别。图中的位置是数据的坐标(数据的X(特征)是二维的,可以直接在坐标上表示),现在我们需要将二维的数据投影到一维,这意味着我们要将其映射到一条直线上面。如上图所示,我们映射到一条直线上面,同时保证:"+","-"类别内部所有的数据投影后结果比较靠近,"+"数据与"-"数据投影后离得较远。很明显,映射到不同的直线就有不同的结果:
为什么我们要做LDA?
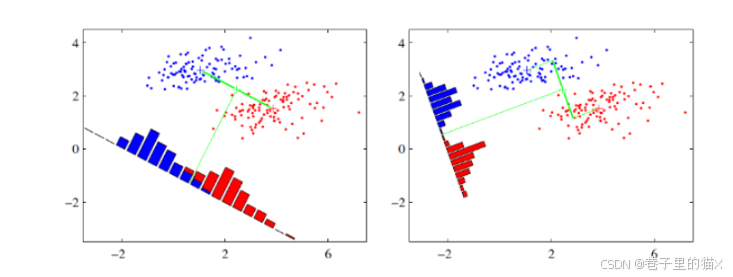
降维最直观的目的是减少数据维度,这样可以减少内存花销和计算时间。但是,降维的目的不仅仅是降维,我们需要信息不能损失。如上所示,当我们数据是二维的时候,我们需要分类的话,很容易使用逻辑回归做一个分类器。但是当我们降维到一维之后,我们的信息肯定有了一定的损失,但是对于我们将降维后的数据进行分类的话,尽量不减少分类精度。简单来说:就是又要速度,又要精度。有时候经过降维还能起到人为增加误差,防止过拟合的作用。
有这么好的事情嘛?在一些情况下确实有:比如上图右侧将二维数据映射到一维后,我们很容易区分哪些数据为蓝色,哪些数据为红色。
二、LDA模型介绍以及推导
我们怎么保证某条直线是最优的。或者我们怎么求出最优的直线。如果在更高维度中,我们怎么得到一个映射关系?
1、LDA二分类的介绍
既然是直接的映射关系,我们可以定义 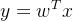
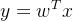
假设我们数据集 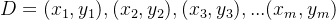
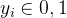
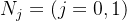
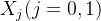
均值 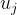
方法 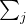
其中𝑗=(0,1)。
由于我们只需要分别两类,最好的分类方法就是将其投影到一条直线即可。我们使用𝑤进行投影。此时,投影后的均值为:
同理方差为:
我们的目标是:同类之间均值尽可能地大,即:
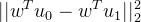
同类之间方差尽可能地小,即:
最小化
综上所述:可以定义我们的优化目标为:
一般我们定义:
为"类内散度矩阵"
为"类间散度矩阵"
因此我们可以将J(w)可以表示为:
由于分子分母都是𝑤的二次项,因此最后的结果和𝑤的大小无关(假设𝑤是最优解,那么𝛼𝑤也一定是最优解)。所以我们可以令:
于是我们的优化目标为:
由拉格朗日乘子法:
𝐹(𝑤)对𝑤求导:
我们可以发现: 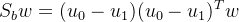
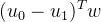
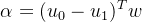
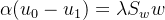
于是:
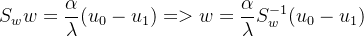
由于 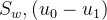
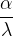
注: 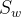
2、推广到多分类
当类别为多个时:
有时候我们也可以写作这样:
其中𝑢为所以样本平均值, 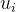
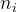
最优公式为:
根据上文的推导,我们有:
假设我们有: ![$W=[w_1,w_2,..w_k]$](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lMjRXJTNEJTVCd18xJTJDd18yJTJDLi53X2slNUQlMjQ%3D)
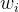
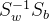
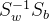
三、LDA的代码
import numpy as np
from sklearn import datasets
from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
X = datasets.load_iris()['data']
Y = datasets.load_iris()['target']
class LDA:
def __init__(self, k_after):
"""
x: 样本x
y: 样本y
n_i: 第i类样本的个数
u_i: 第i类样本均值,格式为{i:[]}
n_label: 样本的类别
k_after: 降维后的维度
k_before: 降维前的维度]
labels: 不同的类别,比如[1,2,3]
"""
self.n_i = {}
self.u_i = {}
self.k_after = k_after
self.k_before = X.shape[0]
self.labels = None
self.sigmas = {}
self.S = None # S_w
self.B = None # S_b
self.w = None
def fit(self, X, y):
self.n = len(np.unique(y))
self.n_label = len(set(y))
labels = np.unique(y)
self.labels = labels
N = X.shape[0] # 样本的个数
means = []
for label in labels:
tmp = np.mean(X[y == label], axis=0) ##第i类的平均u_i
means.append(tmp)
self.u_i[label] = tmp ##记录第i类样本的均值
self.n_i[label] = len(X[y == label]) #记录第i类样本的个数
if len(labels) == 2:
tmp = (means[0] - means[1])
tmp = tmp.reshape(-1, 1) # 转化为(k_before,1)维度的列向量
B = np.dot(tmp, tmp.T) # (u[0]-u[1])(u[0]-u[1])^T
else:
mean_all = np.mean(X, axis=0)
B = np.zeros((X.shape[1], X.shape[1]))
for label in self.u_i:
n_i = self.n_i[label]
tmp = self.u_i[label] - mean_all
tmp = tmp.reshape(-1, 1)
B += n_i * np.dot(tmp, tmp.T)
S = np.zeros((X.shape[1], X.shape[1]))
for label in self.u_i:
u_i = self.u_i[label]
for row in X[y == label]:
tmp = (row - u_i)
tmp = tmp.reshape(-1, 1)
S += np.dot(tmp, tmp.T)
self.S = S
S_inv = np.linalg.inv(S) # 矩阵S_w的逆
S_inv_B = S_inv @ B # S_w*B
diag, p = np.linalg.eig(S_inv_B) ## 特征值,特征向量
ind = diag.argsort()[::-1] ##按照特征值大小排序
diag = diag[ind]
w = p[:, ind] # 按照特征值大小将特征向量排序
self.w = w[:, :self.k_after]
def predict(self, x):
x = np.asarray(x)
return np.dot(x, self.w)
model = LDA(2)
model.fit(X, Y)
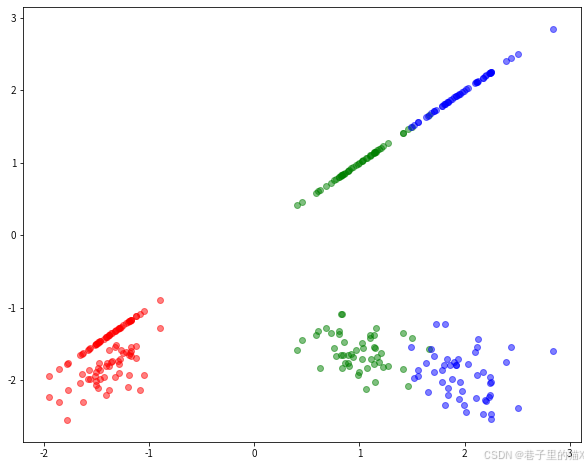
X2=model.predict(X)将数据X,Y映射到一维或者2维的结果如下图所示:
model = LDA(2)
model.fit(X, Y)
X2=model.predict(X)
model2 = LDA(1)
model2.fit(X, Y)
X3=model2.predict(X)
colors = ['red', 'green', 'blue']
fig, ax = plt.subplots(figsize=(10, 8))
for i in range(len(X)):
point=X2[i]
pred=Y[i]
ax.scatter(point[0], point[1], color=colors[pred], alpha=0.5)
ax.scatter(X3[i][0], X3[i][0], color=colors[pred], alpha=0.5)
# ax.scatter(proj[0], proj[1], color=colors[pred], alpha=0.5)
plt.show()from sklearn.discriminant_analysis import LinearDiscriminantAnalysis as LDA
lda = LDA(n_components=2)#设置转换后的维度
X2 = lda.fit_transform(X,Y)
![var(y_k)=E[(y_k-E(y_k))^2]=E[(\alpha^{\top}_kx-\alpha_k^{\top}u)^2]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT92YXIlMjh5X2slMjklM0RFJTVCJTI4eV9rLUUlMjh5X2slMjklMjklNUUyJTVEJTNERSU1QiUyOCU1Q2FscGhhJTVFJTdCJTVDdG9wJTdEX2t4LSU1Q2FscGhhX2slNUUlN0IlNUN0b3AlN0R1JTI5JTVFMiU1RA%3D%3D)
![var(y_k)=E[(\alpha_k^{\top}(x-u))^2]=E[\alpha^{\top}_k(x-u)^2\alpha_k]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT92YXIlMjh5X2slMjklM0RFJTVCJTI4JTVDYWxwaGFfayU1RSU3QiU1Q3RvcCU3RCUyOHgtdSUyOSUyOSU1RTIlNUQlM0RFJTVCJTVDYWxwaGElNUUlN0IlNUN0b3AlN0RfayUyOHgtdSUyOSU1RTIlNUNhbHBoYV9rJTVE)
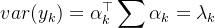
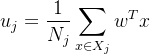
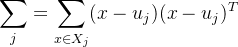
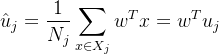
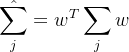
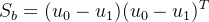
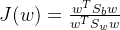
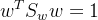
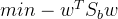
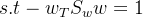
![S_b=\sum_{i,j|i\neq j}[(u_i-u_j)(u_i-u_j)^T]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT9TX2IlM0QlNUNzdW1fJTdCaSUyQ2olN0NpJTVDbmVxJTIwaiU3RCU1QiUyOHVfaS11X2olMjklMjh1X2ktdV9qJTI5JTVFVCU1RA%3D%3D)
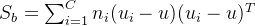
![S_w=\sum_{i}[\sum_{x \in X_i}(x-u_i)(x-u_i)^T]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT9TX3clM0QlNUNzdW1fJTdCaSU3RCU1QiU1Q3N1bV8lN0J4JTIwJTVDaW4lMjBYX2klN0QlMjh4LXVfaSUyOSUyOHgtdV9pJTI5JTVFVCU1RA%3D%3D)