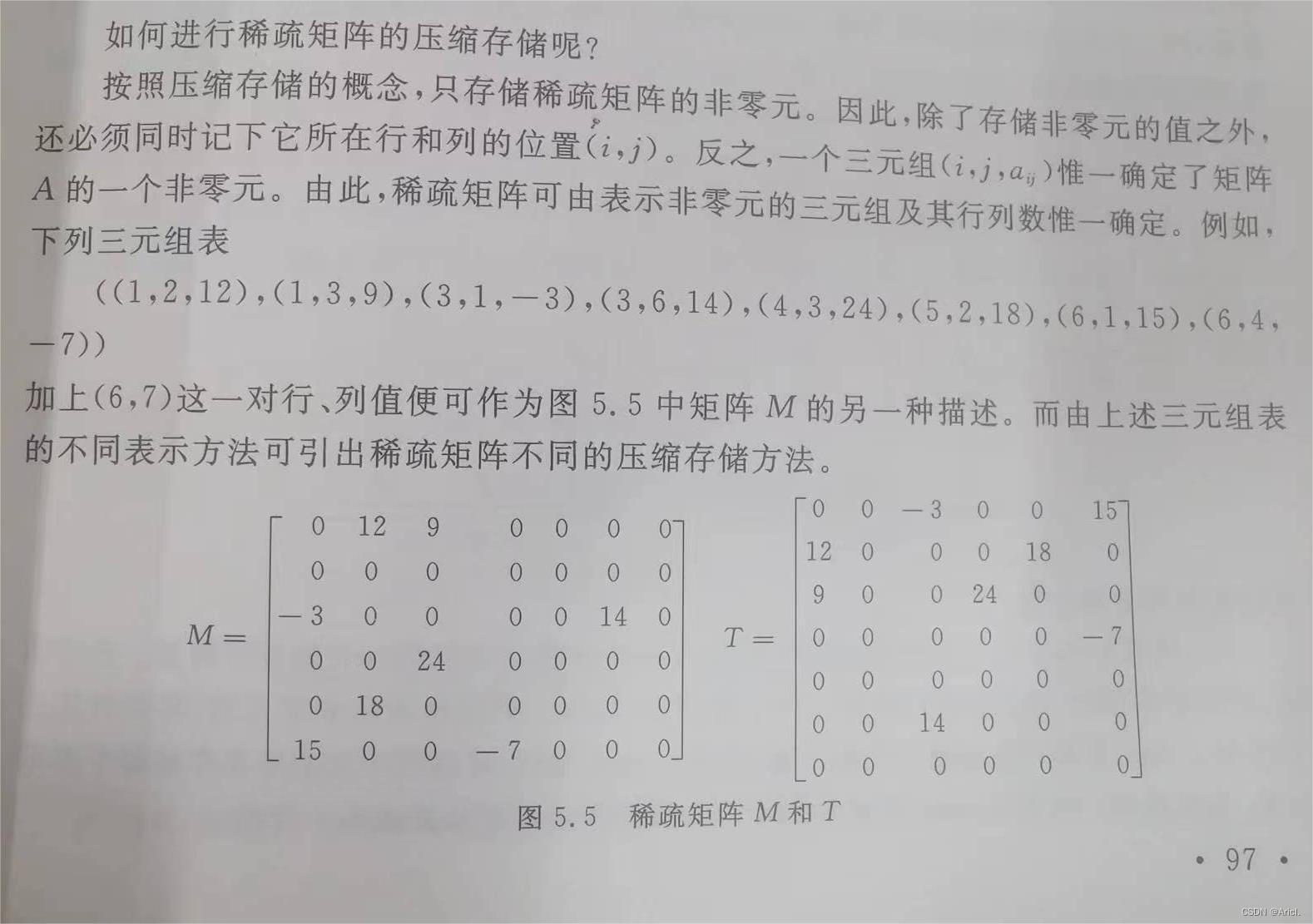
题目:三元组表示的稀疏矩阵快速转置
考点:矩阵的压缩与存储
难度:★★★
稀疏矩阵压缩存储
三元组结构
//三元组结构
typedef struct {
int row;
int col;
int value;
} Term;核心代码
// 转置函数,a为原矩阵,b存放转置后的矩阵
void transpose(Term a[], Term b[]) {
int rowTerms[100], startingPos[100];
int numCols = a[0].col, numRows = a[0].row, numTerms = a[0].value;
b[0].row = numCols; // 转置后的矩阵行数等于原矩阵的列数
b[0].col = numRows; // 转置后的矩阵列数等于原矩阵的行数
b[0].value = numTerms; // 转置后的矩阵非零元素个数等于原矩阵非零元素个数
if (numTerms > 0) {
// 统计每一列非零元素的个数
for (int i = 0; i < numCols; i++)
rowTerms[i] = 0;
for (int i = 1; i <= numTerms; i++)
rowTerms[a[i].col]++;
// 计算转置后每一列非零元素的起始位置
startingPos[0] = 1;
for (int i = 1; i < numCols; i++)
startingPos[i] = startingPos[i - 1] + rowTerms[i - 1];
// 执行转置操作(核心)
for (int i = 1; i <= numTerms; i++) {
int j = startingPos[a[i].col]++;
b[j].row = a[i].col; // 转置后的元素行下标等于原矩阵元素列下标
b[j].col = a[i].row; // 转置后的元素列下标等于原矩阵元素行下标
b[j].value = a[i].value; // 转置后的元素值不变
}
}
}完整代码
#include <stdio.h>
#define MAX_TERMS 100
//三元组结构
typedef struct {
int row;
int col;
int value;
} Term;
// 转置函数,a为原矩阵,b存放转置后的矩阵
void transpose(Term a[], Term b[]) {
int rowTerms[100], startingPos[100];
int numCols = a[0].col, numRows = a[0].row, numTerms = a[0].value;
b[0].row = numCols; // 转置后的矩阵行数等于原矩阵的列数
b[0].col = numRows; // 转置后的矩阵列数等于原矩阵的行数
b[0].value = numTerms; // 转置后的矩阵非零元素个数等于原矩阵非零元素个数
if (numTerms > 0) {
// 统计每一列非零元素的个数
for (int i = 0; i < numCols; i++)
rowTerms[i] = 0;
for (int i = 1; i <= numTerms; i++)
rowTerms[a[i].col]++;
// 计算转置后每一列非零元素的起始位置
startingPos[0] = 1;
for (int i = 1; i < numCols; i++)
startingPos[i] = startingPos[i - 1] + rowTerms[i - 1];
// 执行转置操作(核心)
for (int i = 1; i <= numTerms; i++) {
int j = startingPos[a[i].col]++;
b[j].row = a[i].col; // 转置后的元素行下标等于原矩阵元素列下标
b[j].col = a[i].row; // 转置后的元素列下标等于原矩阵元素行下标
b[j].value = a[i].value; // 转置后的元素值不变
}
}
}
void printMatrix(Term a[]) {
int numRows = a[0].row, numCols = a[0].col, numTerms = a[0].value;
for (int i = 0; i <= numTerms; i++) {
printf("%3d", a[i].value);
printf("%3d", a[i].row);
printf("%3d", a[i].col);
printf("\n");
}
printf("\n");
}
int main() {
Term a[MAX_TERMS];
Term b[MAX_TERMS];
// 初始化原始矩阵
a[0].row = 6;
a[0].col = 6;
a[0].value = 8;
a[1].row = 0;
a[1].col = 0;
a[1].value = 15;
a[2].row = 0;
a[2].col = 3;
a[2].value = 22;
a[3].row = 0;
a[3].col = 5;
a[3].value = -15;
a[4].row = 1;
a[4].col = 1;
a[4].value = 11;
a[5].row = 1;
a[5].col = 2;
a[5].value = 3;
a[6].row = 2;
a[6].col = 3;
a[6].value = -6;
a[7].row = 4;
a[7].col = 0;
a[7].value = 91;
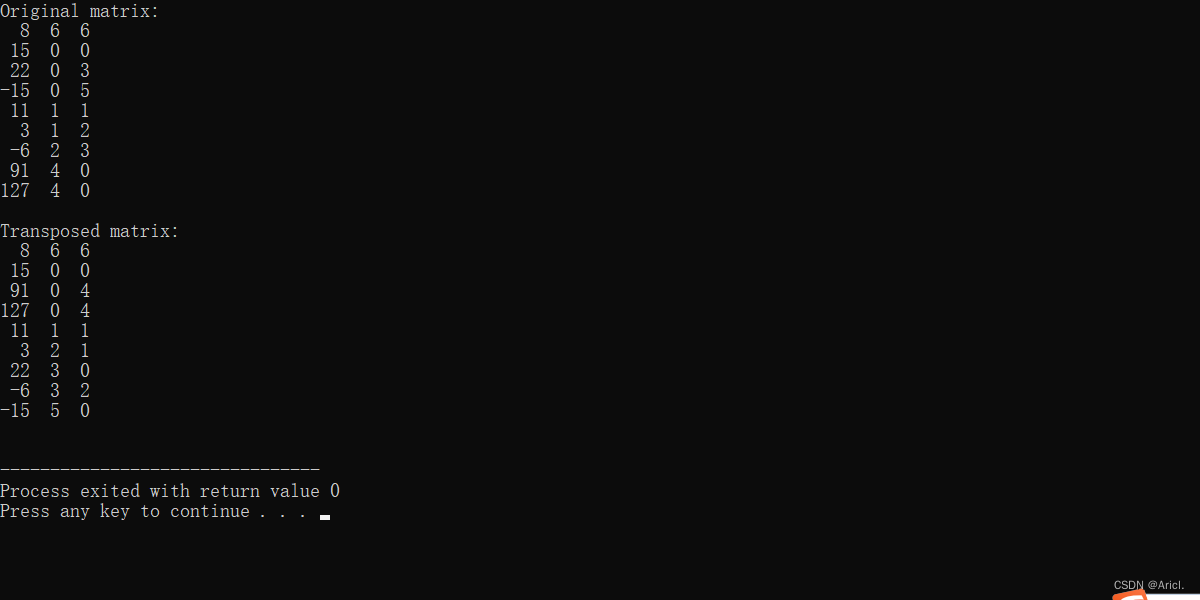
printf("Original matrix:\n");
printMatrix(a);
// 转置矩阵
transpose(a, b);
printf("Transposed matrix:\n");
printMatrix(b);
return 0;
}