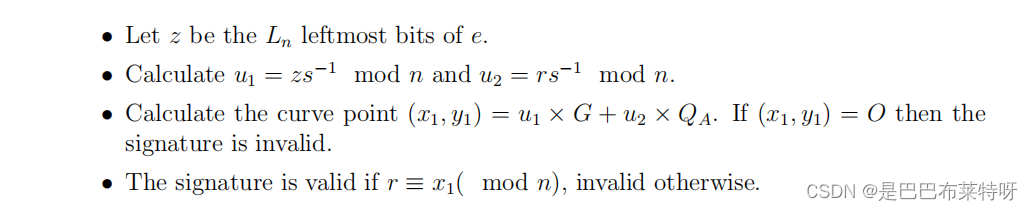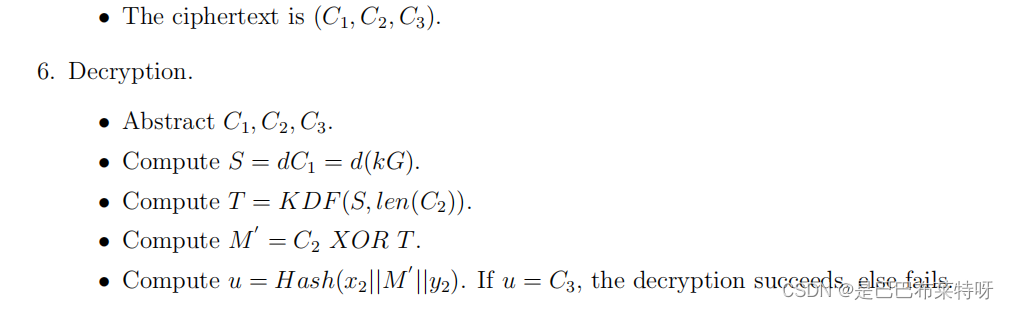Bootstrap

ECC算法与ECDSA签名、SM2签名、SM2加密、ElGamal加密的C/C++实现

一、原理

ECDSA

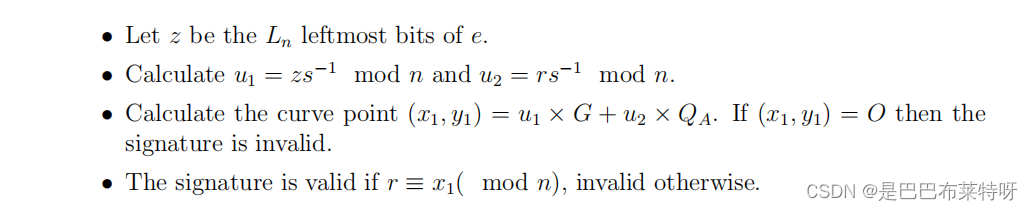
SM2

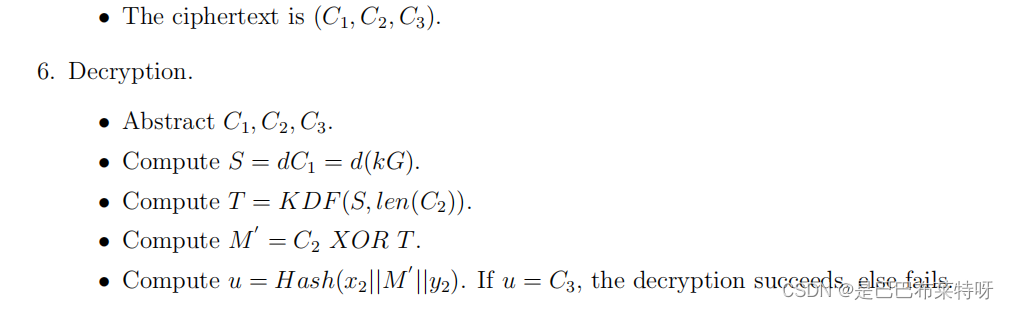
ElGamal

二、C/C++实现

头文件

POperation.h

#ifndef POPERATION_H
#define POPERATION_H

// 定义点的结构
typedef struct {
    long long x;
    long long y;
} Point;

// 定义椭圆曲线的结构
typedef struct {
    long long a, b; // 曲线参数 y^2 = x^3 + ax + b
    long long p;    // 有限域的素数
} EllipticCurve;

// 模逆运算的函数声明
long long mod_inverse(long long a, long long m);

// 点加运算的函数声明
Point point_add(Point P, Point Q, EllipticCurve ec);

// 点乘运算的函数声明
Point point_multiply(long long scalar, Point P, EllipticCurve ec);

#endif // POPERATION_H

ECDSA.h

#ifndef ECDSA_H
#define ECDSA_H

#include "POperation.h" // 包含 EllipticCurve 和 Point 结构的定义

// ECDSA签名函数声明
void ecdsa_sign(char* message, long long d, EllipticCurve ec, Point G, long long n, long long* r, long long* s);

// ECDSA验证函数声明
int ecdsa_verify(char* message, Point Q, EllipticCurve ec, Point G, long long n, long long r, long long s);

// 简单哈希函数声明
long long simple_hash(char* message);

#endif // ECDSA_H

ElGamal.h

#ifndef ELGAMAL_H
#define ELGAMAL_H

#include <gmpxx.h>
#include <vector>
#include <iostream>

// 检测原根
bool is_primitive_root(const mpz_class& g, const mpz_class& p);

// 生成大质数和其原根
void generate_prime_and_primitive_root(mpz_class& p, mpz_class& g);

// 生成公钥和私钥
void generate_keys(mpz_class& p, mpz_class& g, mpz_class& y, mpz_class& x);

// 加密
void encrypt(const mpz_class& p, const mpz_class& g, const mpz_class& y, const mpz_class& m, mpz_class& c1, mpz_class& c2);

// 解密
void decrypt(const mpz_class& p, const mpz_class& x, const mpz_class& c1, const mpz_class& c2, mpz_class& m);

#endif  // ELGAMAL_H

SM2.h

#pragma once
#ifndef SM2_H
#define SM2_H

#include <openssl/evp.h>
#include <openssl/ec.h>
#include <openssl/pem.h>
#include <openssl/err.h>
#include <iostream>
#include <cstring>

// 错误处理函数
void handleOpenSSLErrors();

// 生成SM2密钥对
EVP_PKEY* generateSM2KeyPair();

// SM2签名
bool sm2Sign(EVP_PKEY* pkey, const unsigned char* data, size_t dataLen, unsigned char** sig, size_t* sigLen);

#endif // SM2_H

源文件

POperation.cpp

#include <stdio.h>
#include <stdlib.h>
#include "POperation.h"

//typedef struct {
//    long long x;
//    long long y;
//} Point;
//
//typedef struct {
//    long long a, b; // 曲线参数 y^2 = x^3 + ax + b
//    long long p;    // 有限域的素数
//} EllipticCurve;

// 模逆运算
long long mod_inverse(long long a, long long m) {
    long long m0 = m, t, q;
    long long x0 = 0, x1 = 1;

    if (m == 1) {
        return 0;
    }

    while (a > 1) {
        q = a / m;
        t = m;
        m = a % m, a = t;
        t = x0;
        x0 = x1 - q * x0;
        x1 = t;
    }

    if (x1 < 0) {
        x1 += m0;
    }

    return x1;
}

// 点加运算
Point point_add(Point P, Point Q, EllipticCurve ec) {
    Point R;

    if (P.x == Q.x && P.y == Q.y) { // 点倍运算
        if (P.y == 0) {
            R.x = 0;
            R.y = 0;
            return R;
        }

        long long s = (3 * P.x * P.x + ec.a) * mod_inverse(2 * P.y, ec.p) % ec.p;
        R.x = (s * s - 2 * P.x) % ec.p;
        R.y = (s * (P.x - R.x) - P.y) % ec.p;
    }
    else { // 一般点加运算
        if (P.x == Q.x) {
            R.x = 0;
            R.y = 0;
            return R;
        }

        long long s = (Q.y - P.y) * mod_inverse(Q.x - P.x, ec.p) % ec.p;
        R.x = (s * s - P.x - Q.x) % ec.p;
        R.y = (s * (P.x - R.x) - P.y) % ec.p;
    }

    R.x = (R.x + ec.p) % ec.p;
    R.y = (R.y + ec.p) % ec.p;
    return R;
}

// 点乘运算
Point point_multiply(long long scalar, Point P, EllipticCurve ec) {
    Point result = { 0, 0 }; // 无穷远点
    Point temp = P;

    while (scalar != 0) {
        if (scalar % 2 != 0) {
            if (result.x == 0 && result.y == 0) {
                result = temp;
            }
            else {
                result = point_add(result, temp, ec);
            }
        }

        temp = point_add(temp, temp, ec);
        scalar /= 2;
    }

    return result;
}

ECDSA.cpp

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include "POperation.h"  // 假设之前定义的椭圆曲线结构和函数在这个头文件中
#include "ECDSA.h"

// 简单的哈希函数（仅用于示例）
long long simple_hash(char* message) {
    long long hash = 0;
    while (*message) {
        hash = (hash * 31 + *message) % LONG_MAX;
        message++;
    }
    return hash;
}

void ecdsa_sign(char* message, long long d, EllipticCurve ec, Point G, long long n, long long* r, long long* s) {
    long long z = simple_hash(message); // 获取消息的哈希值

    long long k, x1, y1;
    do {
        k = rand() % (n - 1) + 1;      // 随机数 k
        Point kG = point_multiply(k, G, ec); // 计算 k * G
        x1 = kG.x; y1 = kG.y;

        *r = x1 % n;
    } while (*r == 0);

    long long k_inv = mod_inverse(k, n);
    *s = (k_inv * (z + *r * d)) % n;

    if (*s == 0) {
        ecdsa_sign(message, d, ec, G, n, r, s); // 如果 s 为 0，则重新签名
    }
}


int ecdsa_verify(char* message, Point Q, EllipticCurve ec, Point G, long long n, long long r, long long s) {
    if (r <= 0 || r >= n || s <= 0 || s >= n) {
        return 0; // 验证 r 和 s 是否在合法范围内
    }

    long long z = simple_hash(message); // 获取消息的哈希值

    long long w = mod_inverse(s, n);
    long long u1 = (z * w) % n;
    long long u2 = (r * w) % n;

    Point u1G = point_multiply(u1, G, ec);
    Point u2Q = point_multiply(u2, Q, ec);
    Point P = point_add(u1G, u2Q, ec);

    if (P.x == LONG_MAX && P.y == LONG_MAX) {
        return 0; // 如果 P 是无穷远点
    }

    return (P.x % n == r); // 验证 r 是否等于 P.x mod n
}

ElGamal.cpp

#include <gmpxx.h>
#include <cstdlib>
#include <ctime>
#include <vector>
#include <iostream>
#include "ElGamal.h"

using namespace std;

// 检测原根
bool is_primitive_root(const mpz_class& g, const mpz_class& p) {
    vector<mpz_class> factors;
    mpz_class phi = p - 1;
    mpz_class n = phi;

    // 计算p - 1的所有质因数
    for (mpz_class i = 2; i * i <= n; ++i) {
        if (n % i == 0) {
            factors.push_back(i);
            while (n % i == 0)
                n /= i;
        }
    }
    if (n > 1)
        factors.push_back(n);

    for (mpz_class factor : factors) {
        mpz_class res;
        mpz_powm(res.get_mpz_t(), g.get_mpz_t(), mpz_class(phi / factor).get_mpz_t(), p.get_mpz_t());
        if (res == 1)
            return false;
    }
    return true;
}



// 生成大质数和其原根
void generate_prime_and_primitive_root(mpz_class& p, mpz_class& g) {
    // 生成大质数
    gmp_randclass rr(gmp_randinit_default);
    rr.seed(time(NULL));
    p = rr.get_z_bits(512);
    mpz_nextprime(p.get_mpz_t(), p.get_mpz_t());

    // 寻找原根
    g = 2;
    while (!is_primitive_root(g, p))
        g += 1;
}

// 生成公钥和私钥
void generate_keys(mpz_class& p, mpz_class& g, mpz_class& y, mpz_class& x) {
    // 随机生成大质数p和其原根g
    // 由于寻找原根的效率问题，这里简化为固定的质数和原根
    p = 23;  // 实际应用中应该是大质数
    g = 5;   // 实际应用中应该是p的原根

    // 随机选择私钥x
    x = rand() % (p - 2) + 1;

    // 计算公钥y
    mpz_powm(y.get_mpz_t(), g.get_mpz_t(), x.get_mpz_t(), p.get_mpz_t());
}

// 加密
void encrypt(const mpz_class& p, const mpz_class& g, const mpz_class& y, const mpz_class& m, mpz_class& c1, mpz_class& c2) {
    mpz_class k = rand() % (p - 1) + 1;  // 随机选择k
    mpz_class s;

    // 计算c1
    mpz_powm(c1.get_mpz_t(), g.get_mpz_t(), k.get_mpz_t(), p.get_mpz_t());
    // 计算s (共享密钥)
    mpz_powm(s.get_mpz_t(), y.get_mpz_t(), k.get_mpz_t(), p.get_mpz_t());
    // 计算c2
    c2 = (m * s) % p;
}

// 解密
void decrypt(const mpz_class& p, const mpz_class& x, const mpz_class& c1, const mpz_class& c2, mpz_class& m) {
    mpz_class s, s_inv;

    // 计算s (共享密钥)
    mpz_powm(s.get_mpz_t(), c1.get_mpz_t(), x.get_mpz_t(), p.get_mpz_t());
    // 计算s的逆
    mpz_invert(s_inv.get_mpz_t(), s.get_mpz_t(), p.get_mpz_t());
    // 解密消息
    m = (c2 * s_inv) % p;
}

SM2.cpp

#include "openssl/evp.h"
#include "openssl/ec.h"
#include "openssl/pem.h"

#include <iostream>
#include <cstring>
#include "SM2.h"


// 错误处理
void handleOpenSSLErrors() {
    ERR_print_errors_fp(stderr);
    abort
    ();
}

// 生成SM2密钥对
EVP_PKEY* generateSM2KeyPair() {
    EVP_PKEY_CTX* pctx = EVP_PKEY_CTX_new_id(EVP_PKEY_EC, nullptr);
    EVP_PKEY* pkey = nullptr;
    if (EVP_PKEY_keygen_init(pctx) <= 0) {
        handleOpenSSLErrors();
    }

    if (EVP_PKEY_CTX_set_ec_paramgen_curve_nid(pctx, NID_sm2) <= 0) {
        handleOpenSSLErrors();
    }

    if (EVP_PKEY_keygen(pctx, &pkey) <= 0) {
        handleOpenSSLErrors();
    }

    EVP_PKEY_CTX_free(pctx);
    return pkey;
}

// SM2签名
bool sm2Sign(EVP_PKEY* pkey, const unsigned char* data, size_t dataLen, unsigned char** sig, size_t* sigLen) {
    EVP_MD_CTX* mdctx = EVP_MD_CTX_new();
    EVP_PKEY_CTX* pctx = nullptr;
    bool result = false;
    if (EVP_DigestSignInit(mdctx, &pctx, EVP_sm3(), nullptr, pkey) <= 0) {
        handleOpenSSLErrors();
    }

    if (EVP_DigestSign(mdctx, nullptr, sigLen, data, dataLen) <= 0) {
        handleOpenSSLErrors();
    }

    *sig = (unsigned char*)OPENSSL_malloc(*sigLen);
    if (EVP_DigestSign(mdctx, *sig, sigLen, data, dataLen) <= 0) {
        handleOpenSSLErrors();
    }
    else {
        result = true;
    }

    EVP_MD_CTX_free(mdctx);
    return result;
}

ECCtest.cpp

 main.c
//#include "ecc.h"
//#include <stdio.h>
//
//int main() {
//    EllipticCurve ec = {/* 初始化曲线参数 */ };
//    Point p = {/* 初始化点 */ };
//
//    // 测试点乘
//    Point result = point_multiply(2, p, ec);
//    printf("Result of Point Multiply: (%lld, %lld)\n", result.x, result.y);
//
//    // 测试ECDSA签名和验证
//
//    return 0;
//}

#include<cstdio>
#include <gmp.h>
#include <time.h>
//#include "openssl/ec.h"
//#include "openssl/evp.h"

#include "POperation.h"
#include "SM2.h"
#include "ECDSA.h"
#include "ElGamal.h"

#define P "23"
#define G "5"


int main() {
     示例：定义椭圆曲线参数和点
    //EllipticCurve ec = { 1, 6, 11 }; // 曲线 y² = x³ + x + 6 (mod 11)
    //Point P = { 2, 4 }; // 初始点
     执行点乘运算
    //Point Q = point_multiply(3, P, ec);
    //printf("3P = (%lld, %lld)\n", Q.x, Q.y);

     执行点加运算
    //Point R = point_add(P, Q, ec);
    //printf("P + 3P = (%lld, %lld)\n", R.x, R.y);



    //auto key = EC_KEY_new_by_curve_name(NID_secp256k1);
    //EC_KEY_generate_key(key);

    //unsigned char* pub_key = nullptr;

    //auto size = i2o_ECPublicKey(key, &pub_key);
    //for (int i = 0; i < size; ++i) {
    //    std::printf("%02x", pub_key[i]);
    //}

    // EC_KEY_free(key);









    ECDSA sign and verify
    // // 定义椭圆曲线参数（简化版secp256k1）
    //EllipticCurve ec = { 0, 7, 17 };  // y^2 = x^3 + 7 (mod 17)
    //Point G = { 1, 1 };              // 基点G
    //long long n = 19;              // 基点的阶

     定义私钥（随机选取，但必须小于n）
    //long long d = 13; // 私钥

     计算公钥
    //Point Q = point_multiply(d, G, ec);

     要签名的消息
    //char message[] = "Hello, ECDSA!";

     签名
    //long long r, s;
    //ecdsa_sign(message, d, ec, G, n, &r, &s);
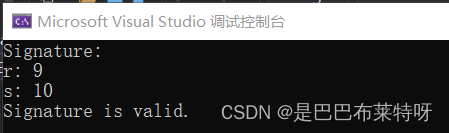
    //printf("Signature:\n");
    //printf("r: %lld\n", r);
    //printf("s: %lld\n", s);

     验证
    //int valid = ecdsa_verify(message, Q, ec, G, n, r, s);
    //if (valid) {
    //    printf("Signature is valid.\n");
    //}
    //else {
    //    printf("Signature is invalid.\n");
    //}



    SM2加密和签名
    //OpenSSL_add_all_algorithms();
    //ERR_load_crypto_strings();
     生成密钥对
    //EVP_PKEY* pkey = generateSM2KeyPair();

     要签名的数据
    //const char* data = "Hello, SM2!";
    //unsigned char* sig = nullptr;
    //size_t sigLen = 0;

     签名
    //if (sm2Sign(pkey, (const unsigned char*)data, strlen(data), &sig, &sigLen)) {
    //    std::cout << "Signature successful!" << std::endl;
    //}
    //else {
    //    std::cout << "Signature failed!" << std::endl;
    //}

     清理
    //OPENSSL_free(sig);
    //EVP_PKEY_free(pkey);
    //EVP_cleanup();
    //ERR_free_strings();




    //ElGamal测试
    mpz_t p, g, x, y, m, c1, c2, decrypted_m;
    mpz_inits(p, g, x, y, m, c1, c2, decrypted_m, NULL);

    // 设置p和g
    mpz_set_str(p, P, 10);
    mpz_set_str(g, G, 10);

    // 生成密钥
    generate_keys(p, g, x, y);
    gmp_printf("Public Key (y): %Zd\n", y);
    gmp_printf("Private Key (x): %Zd\n", x);

    // 设置消息m
    mpz_set_ui(m, 13); // 设置一个示例消息

    // 加密消息
    encrypt(p, g, y, m, c1, c2);
    gmp_printf("Encrypted Message (c1, c2): (%Zd, %Zd)\n", c1, c2);

    // 解密消息
    decrypt(p, x, c1, c2, decrypted_m);
    gmp_printf("Decrypted Message: %Zd\n", decrypted_m);

    mpz_clears(p, g, x, y, m, c1, c2, decrypted_m, NULL);


    return 0;
}

三、运行结果

POperation测试

SM2测试

ECDSA测试

悦读

道可道，非常道；名可名，非常名。 无名，天地之始，有名，万物之母。 故常无欲，以观其妙，常有欲，以观其徼。 此两者，同出而异名，同谓之玄，玄之又玄，众妙之门。

最新收录
华为OD机试 - 求最小公倍数（Python/JS/C/C++ 牛客练习题 HJ108）
聊一聊 .NET高级调试 内核模式堆泄露
2023年第十四届蓝桥杯C++B组复盘
JMeter进行WebSocket压力测试
8位微控制器上的轻量级SM2加密算法实现：C语言详细指南与完整代码解析
Cacheline技术浅析
Oracle 低代码平台 Apex 最新版本 23.2 安装过程
python爬虫用redis去重多种方法
蓝桥杯基础练习 回形取数（Java）---东北 墙
11.Docker 之分布式仓库 Harbor
;