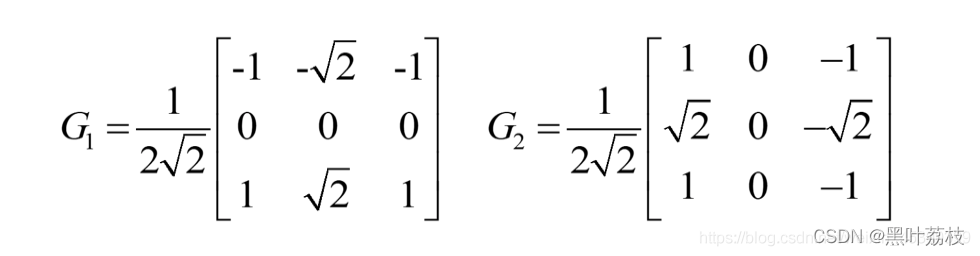本文转载自
【边缘检测——sobel索伯算子 数学原理和应用】https://mbd.baidu.com/ma/s/kJPWKq8G
索伯算子(sobel operator)常用于边缘检测,在粗精度下,是最常用的边缘检测算子,以广泛应用几十年。sobel算子由两个3X3的卷积核构成,分别用于计算中心像素邻域的灰度加权差。分为垂直方向和水平方向的索伯滤波器Gx and Gy。
sobel 算子的用途主要为:
边缘检测时: Gx用于检测纵向边缘, Gy用于检测横向边缘.
计算法线时: Gx用于计算法线的横向偏移, Gy用于计算法线的纵向偏移
sobel算子应用时进行给定图像的卷积操作,卷积为计算图像大矩阵周围像素和滤波器矩阵对应位置元素的乘积, 然后把结果相加到一起, 最终得到的值就作为该像素的新值, 这样就完成了一次
卷积,之后继续移动卷积核,直到把大矩阵每个位置都运算完毕,因为相邻像素卷积结果一般具有相似输出,会产生大量冗余信息,一般为减少输出值会进行求取最大小值或者平均值的池化操作。
经sobel算子处理的图像(图像来源于网路,侵删)
值得注意的是,一般卷积操作会伴随卷积核的翻转,而sobel却不需要翻转,因为绕中心点旋转180°,并不影响结果。
sobel算子的卷积核的值是如何确定的呢?其实并不是经验数值,而是具有严格的数学推导,大部分教科书停留在对算子的直观解释上,一般描述为隔行或隔列的差分运算,然后做中心像素位置的2倍加权。实际上,并不是现行教科书上描述的简单的隔行/列的差分运算,中心像素位置也并未参与运算。目前流传的说法中以科学网 彭真明老师提出的曼哈顿距离表述的推导更为准确。
以下对这一过程进行简单推导:
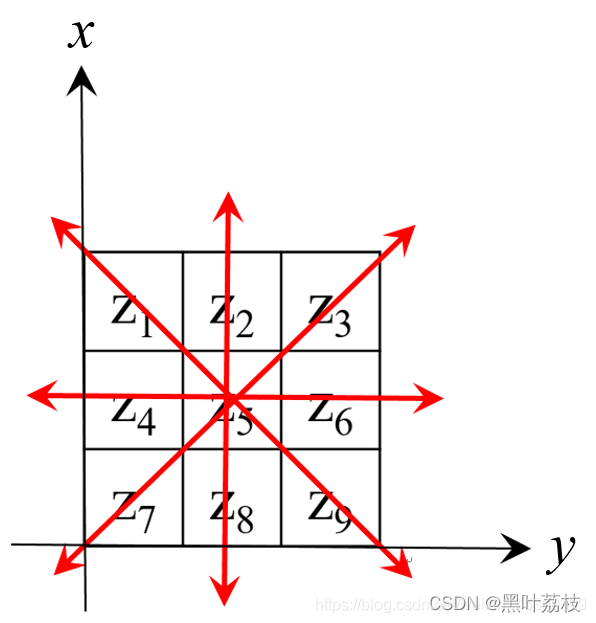
对中心像素Z5求取多个方向的灰度差分,对于Z5的8个邻域,分为4个方向,即对角线和水平垂直4个方向对: (z1, z9) ,(z2, z8), (z3, z7), (z6, z4)。
定义一个给定邻域方向梯度矢量g的幅度为
|g| = <像素灰度差分>/<相邻像素的距离>
这里特别注意的是,距离为曼哈顿距离,而非欧氏距离(欧氏距离将推导出Frei和Chen(1991)提出的边缘检测器,见附图3)
由曼哈顿距离得出,相邻对角线像素的距离为2,水平与垂直距离为1,即在中心像素周围邻域像素的对角线距离为4,垂直水平距离为2,带入上述梯度矢量g计算公式求平均梯度矢量有:
G = {(z3-z7)/4 * [1, 1]+ (z1-z9)/4 * [-1, 1]+ (z2-z8)/2 * [0, 1]+ (z6-z4)/2 * [1, 0] }/4
式中, 4个单位向量 [1, 1],[-1, 1],[0, 1], [1, 0] 控制差分的方向.
上式展开后,有
G = [(z3- z7- z1+ z9)/4 + (z6-z4)/2, (z3- z7+ z1- z9)/4 + (z2-z8)/2] /4
为保留低位字节和加速运算,去除分母,即扩大16倍。
这样,计算公式变为:
G’ = 16*G
= [z3 - z7- z1+ z9 + 2*( z6 - z4), z3 - z7 + z1- z9 + 2*( z2-z8)]
= [z3 + 2z6 + z9 - z1 - 2z4-z7, z1 + 2z2 + z3 - z7 - 2z8 - z9]
按x-y方向,可分别写成:
G’x = (z3 + 2z6 + z9) - (z1 + 2z4 + z7)
G’y = (z1 + 2z2 + z3) - (z7 + 2z8 + z9)
由上式可得sobel垂直水平卷积核。
附图3:
参考:
http://blog.sciencenet.cn/blog-425437-1139187.html
https://baike.baidu.com/item/索伯算子/22735660?fr=aladdin
https://www.cnblogs.com/freeblues/p/5738987.html
https://www.zhihu.com/question/49376084