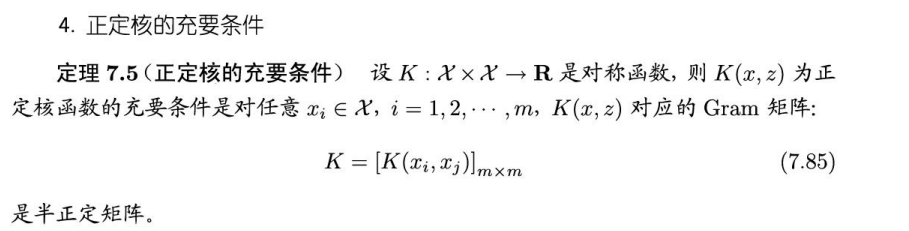本节介绍非线性支持向量机与核函数,这部分还是比较难的数学功底需要比较深厚。
目录
前言
对解线性可分问题,线性支持向量机是一种非常好的分类方法,但是在很多情况中都是线性不可分的,那么又该怎么处理呢?
数学家最常用的思想就是将问题转化成以被解决的问题,那对于非线性可分的问题,怎样转化成线性可分的问题呢?
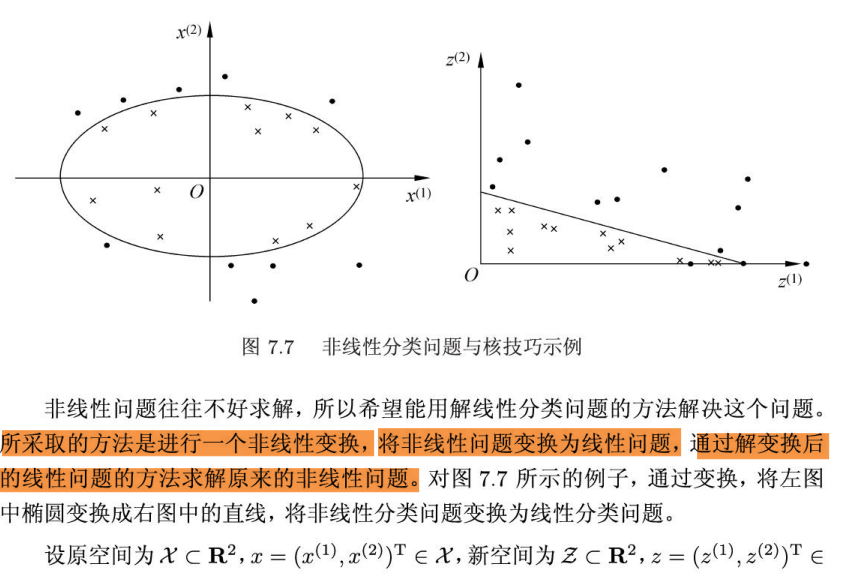
这里就有一个重要结论:在低维一个线性不可分的数据集映射到高维线性可分的概率越大,如果映射到无穷维,可认为线性可分的概率为一,即一定能找到一个超平面使数据可分。
这就是非线性支持向量机与核函数的思想应用。
一、为什么映射到高维线性可分。
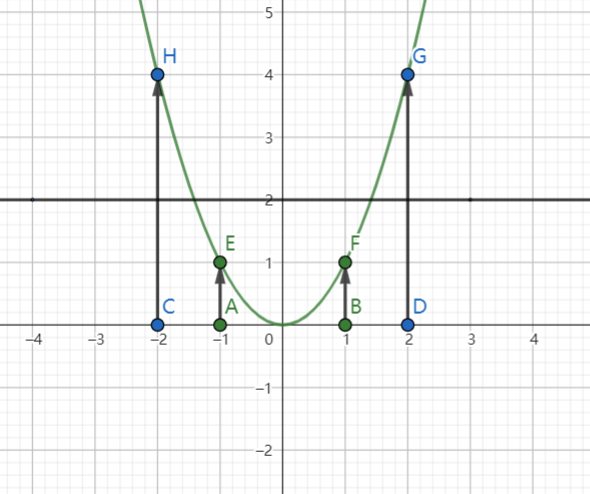
初始有A、B、C、D四个点,颜色代表分类,在一维的角度我们没法找到一个点使得两类点线性可分,但经过y = x^2的映射到二维空间,我们可以看到数据集线性可分了。一维映射到二维。
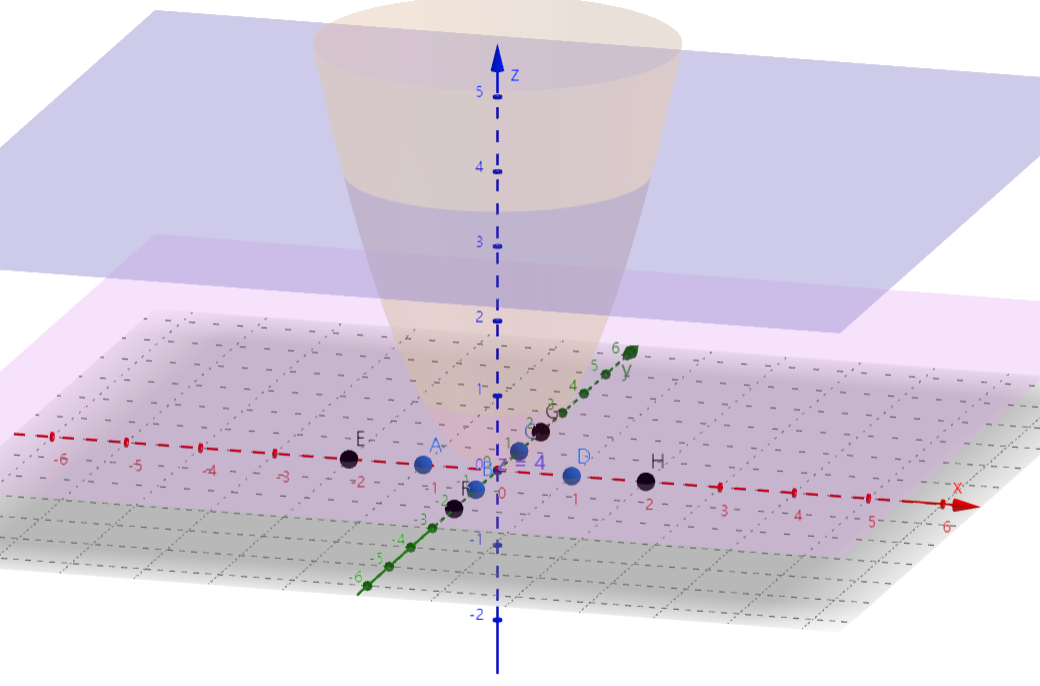
二维映射到三维。
二、核技巧
三、正定核的充要条件
这部分还是有看不懂,数学基础知识还是比较弱,只简单介绍少核函数需要满足什么条件。
这里用线性代数的知识很好证明,不多说。Gram矩阵就是内积矩阵,所以是对称矩阵。
四、常用核函数
五、非线性支持向量机
总结
主要介绍非线性支持向量机与核函数方法,为什么核技巧要用到原问题的对偶问题来求解呢?因为可以大幅度减少计算量。下一节介绍优化算法,呜呜真是太难了,坚持住!