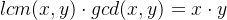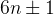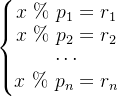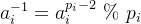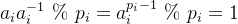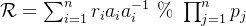2022 年省赛:我估计 48.5 分左右 (满分 150)。广东总共 78 个省一,我只排到了第 33 (42.3%)
2022 年国赛:最后一道大题没时间写 —— 暴力就能满分的题,血亏,最后国三
2023 年省赛:居然是全省第二 (广东 B 组省一共 91 人,前 2.1%),差点没把我笑死
2023 年国赛:倒数第二题交的时候多了一个 print,只拿了国二
2024 年省赛:F 题列表越界访问了……省一但没什么好名次。赛前只是复习了 5 天,感觉太久没练新题题感下降了不少。9 月读研了没时间刷新题目,加上本校不办赛点了,应该不参加国赛了
在本篇文章中,我将从“知识预备”、“刷题网站”、“函数模板”三个方面为大家讲解怎样准备蓝桥杯 Python 组的比赛 —— 为什么不三连?!?
知识预备
开发环境
官方要求的是 IDLE,截至 2023 都是可以用 PyCharm 的 (具体还是要找组委会问清楚,不要问“能不能用”,要问“算不算作弊”)
2024.03.30 组委会 - 张老师:不能用 PyCharm,用了不算作弊
2024.04.03 组委会 - 刘老师:用 PyCharm 按作弊处理,函数名称补全不算作弊
2024.04.12 组委会 - 陈老师 (粤 / 宁):用 PyCharm 不算作弊,但是结果自负
2024.04.12 组委会 - 刘老师:不能用
组委会没统一口径真的难顶
可以使用以下代码查看自己的 Python 版本
import sys
print(sys.version_info[:3])以下是 PyCharm 和 IDLE 常用的快捷键 (如果以后比赛可以用 PyCharm 的话)
| PyCharm: | |||||||||
| Ctrl + F | 查找 | Tab | 加缩进 | Ctrl + J | 代码提示 | Ctrl + Alt + L | 格式化文件 | ||
| Ctrl + R | 替换 | Shift + Tab | 减缩进 | Ctrl + / | 注释 | Ctrl + Alt + O | 导入优化 | ||
| F11 | 书签 | Ctrl + Shift + F10 | 运行 | ||||||
| IDLE: | |||||||||
| Ctrl + F | 查找 | Ctrl + ] | 加缩进 | Ctrl + N | 文件编辑 | Alt + M | 代码模块 | F1 | 帮助文档 |
| Ctrl + H | 替换 | Ctrl + [ | 减缩进 | F5 | 运行 | ||||
IDLE 代码提示
打开 IDLE 的代码提示,需要修改以下文件的代码 (假设 Python 的安装路径为 ~):
- ~/Lib/idlelib/autocomplete.py:import <目标模块>
- ~/Lib/idlelib/config-extensions.def:popupwait= 0
帮助文档 (推荐)
IDLE 的代码提示有限,任何别名都会导致代码提示失效。比如 x = collections.Counter,x 会无法识别。所以建议结合 help("modules")、help、dir 函数使用
模块名称:help("modules")
关键字列表:keyword.kwlist
内置函数:dir(builtins)
函数 / 类 / 模块文档:help(func_cls_mod)
忘记某个函数的用法时,可以使用 help 函数查看说明文档
help 也可以用于查找模块的函数列表
类 / 模块属性:dir(cls_mod)
dir 函数既可查看模块的函数 / 对象列表,也可以查看对象的属性 / 方法列表
算法知识
具体考点可以看这篇文章:
蓝桥杯大赛软件类备赛指南
【蓝桥杯比赛】视频教程(入门学习+算法辅导)
贪心算法的话,比较玄学,练习为主:LeetCode:贪心算法题集
Python 组和其它组的不同点在于,代码简洁在很多情况下约等于高效,例如:
- 求一个列表的最大值及其索引时,暴力的 max + index 比 for 循环更快
- 使用 class 写的线段树减少运算量时,运行时间反倒比暴力写法还长 (也有可能是我的类写得太烂)
所以在准备 Python 组的比赛时,一些算法是不需要学的。同时,因为 Python 的效率并不是和运算量直接挂钩,所以还要多对比不同写法所花费的时间:
import math
class timer:
def __init__(self, repeat: int = 1, avg: bool = True):
self.repeat = max(1, int(repeat) if isinstance(repeat, float) else repeat)
self.avg = avg
def __call__(self, func):
import time
def handler(*args, **kwargs):
t0 = time.time()
for i in range(self.repeat): func(*args, **kwargs)
cost = (time.time() - t0) * 1e3
return cost / self.repeat if self.avg else cost
return handler
# 求 x! 关于 1398173074 的余数
mod = 1398173074
@timer(repeat=2)
def fun1(x):
return math.factorial(x) % mod
@timer(repeat=10)
def fun2(x):
result = 1
for i in range(2, x + 1):
result = result * i % mod
return result
for f in [fun1, fun2]:
print(f'Cost:\t{f(540880):.2f}\tms')
Cost: 3238.52 ms
Cost: 91.90 ms
对于 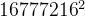
比赛中题目的测评时间一般是 10 s 以上 (甚至有 30 s),解题时根据问题规模设计好代码的时间复杂度
然后比赛答题时,一定要过一遍整份考题,因为题目的难度不一定是递增的 —— 要知道我 22 年国赛看见全卷最简单的题在最后、分值最高、还没时间做有多绝望
标准库
学标准库之前,首先还得会 Python 的一些基础数据类型:str、list、tuple、dict、set
还有文件相关的操作,填空题可能会碰到需要读取 .txt 的题目,运气不好的话碰到超长文本的是复制不了的 (超出剪切板长度限制)
而且对于类和实例的认识是越深越好 (如类似 __call__ 这种名字的类方法),这有利于你直接阅读源代码,提高对标准库的认知
网课:【Python教程】《零基础入门学习Python》最新版
tips:
- 学好迭代器 (包括生成器) 的概念和用法,迭代器的内存占用远远小于 list 等容器,可以大幅度提升性能
- 代码越多越容易出错,利用标准库的函数简化你的代码
- Python 的 for、while 效率低下,尽可能利用标准库的函数规避这些循环
- 避坑 statistics 库,底层代码都是 Python 实现的,效率上求平均不如 sum,中位数和 sorted 差不多,众数和 Counter 差不多
如果不知道以下的这些代码怎么用,可以在我的主页搜索相关代码,就可以看到相应的例题
二分 bisect
对于有序数列 (也可以是有 __lt__ 方法的对象),二分法查找的速度会快很多
| 升序 | bisect_left(array, x) | 二分法查找x | 已有x时 → x位置 |
| bisect(array, x) | 已有x时 → x右侧 | ||
| insort(array, x) | 二分法插入x | ||
复数 cmath
| 数值操作: | |||||||
| pi | п | isnan(z) | 判断nan | isinf(z) | 判断inf | isfinite(z) | 是否有限 |
| tau | 2п | nan | nan | inf | ∞ | isclose(a, b) | 是否相近 |
cmath 库是复数运算库,在蓝桥杯比赛里面很实用
蓝桥杯经常出现一些 x-y 坐标系求两点间距离、角度的题,利用复数的模、相角求解可以简化代码和提高运算速度
| 属性访问: | |
| z.real | 复数实部 |
| z.imag | 复数虚部 |
| z.conjugate() | 对应共轭复数 |
| abs(z) | 复数的模 |
| phase(z) | 复数相角 (-п, п] |
| 运算函数: | |||
| rect(r, phi) | 极坐标 → 复数 | ||
| polar(z) | 复数 → 极坐标 (r, φ) | ||
| sqrt(z) / isqrt(z) | z ^ 0.5 | pow(z, a) | z ^ a |
| sin(z) / cos(z) / tan(z) | 三角函数 | 正运算 | |
| asin(z) / acos(z) / atan(z) | 逆运算 | ||
| exp(z) / log(z, base=e) | 指数运算 | ||
容器 collections
Counter 可快速统计序列 (如字符串) 中的元素,而 deque 优化了队列端点的相关操作 (还可以自动限定长度)
| 计数器: | |||
| Counter(var, **kwargs) | 实例化计数器 (dict子类) | ||
| 实例方法 | elements() | 返回元素迭代器 | |
| most_common(int=None) | 返回指定数量高频值 | ||
| update(var, **kwargs) | 更新计数器 | 加法 | |
| subtract(var, **kwargs) | 减法 | ||
| 队列: | ||
| deque(iter, maxlen) | 实例化限长队列 | |
| 实例方法 | append / appendleft(obj) | 入队 |
| extend / extendleft(iter) | 迭代入队 | |
| pop / popleft() | 出队 | |
| insert(i, obj) | 插入元素 | |
| count(obj) | 返回元素出现次数 | |
| index(obj, start, end) | 返回元素的位置 | |
拷贝 copy
主要是 deepcopy 比较有用,特别是对于维度大于 1 的 list、多重 dict 的 copy
| copy(obj) | 浅拷贝变量 |
| deepcopy(obj) | 深拷贝变量 |
日期 datetime
蓝桥杯有时会有一些关于日期的题,这个库配合 try - except 语句可以判断某个日期的合法性
| 日期: | ||
| datetime(year, month, day, hour=0, minute=0) | 实例化日期 | |
| 类方法 | today() | 当前日期 |
| fromtimestamp(t) | 秒数 → 日期 | |
| strptime(date_string, format) | 字符串 → 日期 | |
| 实例方法 | date() | 返回日期实例 |
| time() | 返回时间实例 | |
| weekday() | 返回0 ~ 6 (Mon ~ Sun) | |
| timetuple() | 返回时间元组 | |
| timestamp() | 返回秒数 | |
| replace(year, month, day, hour, minute) | 更新日期 | |
两个 datetime 实例 (日期) 相减可以得到 timedelta 实例 (时间差)
| 时间差: | ||
| timedelta(days, seconds, minutes, hours, weeks) | 实例化时间差 同类可加减比较,可与int乘除 | |
| 实例属性 | days | 天数 |
| seconds | 秒数 | |
函数 functools
lru_cache 用于记忆化 DFS 时,可以自动存储函数在不同参数下的运行结果,效率比自己写的 dict 快很多
| partial(func, *args, **kwargs) | 返回部分应用给定参数的函数 |
| reduce(func, seq, init=None) | 返回序列值逐次二元运算的结果 (比itertools.accumulate快) |
| lru_cache(maxsize=None) | 返回结果缓存修饰器 (记忆化DFS神器) |
堆 heapq
堆在解决“前 n 大”、“前 n 小”的问题上有很高的效率
这个库只提供了小根堆的函数 (大根堆都是隐藏函数),要使用大根堆的话对所有元素取负就行了
heapq 不仅可以针对数值类型,还可以用于有 __lt__ 方法的自定义类
| 小根堆: | |
| heapify(list) | 原地小根堆化 |
| heappush(heap, item) | 添加堆结点 |
| heappop(heap) | 弹出堆顶,并重排 |
| merge(*sorted, key, reverse) | 合并有序数列 |
| nsmallest(n, iter, key) | 返回升序前n元素 |
| nlargest(n, iter, key) | 返回降序前n元素 |
| heapreplace(heap, item) | pop → push |
| heappushpop(heap, item) | push → pop |
迭代 itertools
迭代工具库封装了一些迭代操作,避免使用 Python 的 for 循环可以大大加速
| 运算: | ||
| accumulate(iter, oper=int.__add__) | 返回前缀和 | |
| groupby(iter, key) | 返回分组结果 (dict) | |
| permutations(iter, k) | 返回全排列 | |
| combinations(iter, k) | 返回全组合 | 元素无重复 |
| combinations_with_replacement(iter, k) | 元素有重复 | |
| 过滤: | ||
| compress(iter, bool_seq) | 返回压缩过滤序列 | |
| takewhile(filter, iter) | 筛选满足条件的值 | while - break |
| dropwhile(filter, iter) | 滤除满足条件的值 | |
| 迭代器: | ||
| count(start, step) | 无尽线性序列 | |
| product(*iter) | 返回笛卡尔积 | |
| islice(iter, start, stop, step) | 返回切片迭代器 | |
| chain(*iter) | 返回级联迭代器 | |
| cycle(iter) | 返回循环迭代器 | 级联迭代器 |
| repeat(obj, times=None) | 重复元素 | |
实数 math
| 数值操作: | |||||||
| pi | п | isnan(x) | 判断nan | isinf(x) | 判断inf | isfinite(x) | 是否有限 |
| tau | 2п | nan | nan | inf | ∞ | isclose(a, b) | 是否相近 |
开方的速度:math.isqrt 函数 (取整) > math.sqrt 函数 > 运算符
求幂的速度:
- 取整:运算符 > pow 函数 > int(math.pow) > 自编二分快速幂 (无取模)
- 无取整:math.pow > 运算符 > pow 函数 > 自编二分快速幂 (无取模)
- 取模:pow 函数 > 自编二分快速幂
当用到取模的幂运算时,只有内置的 pow 函数提供了 “mod” 参数,math.pow 则没有
| 运算函数: | |||
| sqrt(x) / isqrt(x) | x ^ 0.5 | pow(x, a) | x ^ a |
| factorial(x) | x! | prod(iter) | 累乘 |
| perm(n, k) | 排列数,P = n! / (n - k)! | ||
| comb(n, k) | 组合数,C = P / k! | ||
| sin(x) / cos(x) / tan(x) | 三角函数 | 正运算 | |
| asin(x) / acos(x) / atan(x) | 逆运算 | ||
| exp(x) / log(x, base=e) | 指数运算 | ||
| ceil(x) / floor(x) | 取整 | ||
| degrees(x) / radians(x) | 弧度 <-> 角度 | ||
| dist(p, q) | 欧式距离 | 点 → 点 | |
| hypot(*coord) | 点 → 原点 | ||
| gcd(a, b) / lcm(*int) | 最大公约数 / 最小公倍数 | ||
其中的 lcm 只有在 Python 3.9.0 以上才可以用,而 gcd 的用法也在 Python 3.9.0 更新为 gcd(*int),可以求解多个整数的最大公约数。准备一个 Python 3.9.0 可以在填空题省下不少功夫
正则 re
我觉得这是个必学的库,在字符串的处理上有很高的效率
会这个的话考试碰上乱杀 (比如 22 年国赛的内存管理),不会的话等着被乱杀
| 正则表达式: | |||||
| . | 换行符之外的任意字符 | ||||
| \d | 数字 (\D表非) | ||||
| \s | 空白符 (\S表非) | ||||
| \w | 字母、数字、下划线、汉字 (\W表非) | ||||
| ^ | 置于开头,只匹配前缀 | ||||
| $ | 置于结尾,只匹配后缀 | ||||
| | | 或 | ||||
| ( ) | 捕获组 (findall有效 / <Match>.group(1)读取) | ||||
| [ ] | 字符类 | - | 在中间则表范围 (\u4e00-\u9fa5表中文) | ||
| ^ | 在首位表不在其中的字符 | ||||
| { } | 数字 / 范围表前一字符重复次数 | ||||
| * | 等价 {0,} | + | 等价 {1,} | ? | 等价 {0,1} |
| 编译标志RegexFlag: | |||
| I | 忽略字母大小写 | M | '^'、'$'跨行匹配 |
| S | '.'可匹配换行符 | X | 忽略表达式中的空格和注释 |
| 匹配函数: | |
| compile(pattern, flags) | 返回编译的正则表达式 |
| findall(pattern, string, flags) | 返回匹配的字符串列表 |
| sub(pattern, repl, string, count, flags) | 替换子字符串 |
| split(pattern, string, maxsplit, flags) | 分割字符串 |
| 匹配实例: | ||
| search(pattern, string, flags) | 返回匹配结果 | |
| match(pattern, string, flags) | 返回前缀的匹配结果 | |
| finditer(pattern, string, flags) | 返回所有的匹配结果 | |
| 实例方法 | group(i=0) / groups() | 匹配内容 |
| start(i=0) | 起始位置 | |
| end(i=0) | 结束位置 | |
| span(i=0) | 匹配范围 | |
时间 time
经过 24 年省赛,发现 time 库还是有必要学的
时间元组的相关内容不用背,了解就行,help(time.struct_time) 和 help(time.strptime) 可以查
| 时间元组struct_time: | ||
| tm_sec | %S | 0~61 |
| tm_min | %M | 0~59 |
| tm_hour | %H | 0~23 |
| tm_mday | %d | 1~31 |
| tm_mon | %m | 01~12 |
| %b | Jan ~ Dec | |
| %B | January ~ December | |
| tm_year | %Y | 2001 |
| tm_wday | %a | Mon ~ Sun (0 ~ 6) |
| %A | Monday ~ Sunday | |
| tm_yday | 年中第几天 | 1 ~ 366 |
| tm_isdst | 夏令时真值 | 0,1,-1 (代表夏令时) |
| 时间转换: | |||
| 秒数 | ctime(seconds=None) | 秒数 → 字符串 | %a %b %d %H:%M:%S %Y |
| gmtime(seconds=None) | 秒数 → 时间元组 | 格林威治时间 | |
| localtime(seconds=None) | 当地时间 | ||
| 时间元组 | mktime(t_tuple) | 时间元组 → 秒数 | |
| strftime(format, t_tuple) | 时间元组 → 字符串 | ||
| 字符串 | strptime(str, format) | 字符串 → 时间元组 | |
刷题网站
经过 2022 的省赛国赛,还是得说:要相信 Python 暴力算法的力量
在刷题的时候,要把有价值的题目记录下来 (e.g. 写博客),方便日后复习
如果没时间记录的话,可以跟着我的 数据结构与算法专栏 练习、复习
蓝桥杯练习系统
网站链接:http://lx.lanqiao.cn/problemsets.page
“基础练习”里面虽然都是无脑题,但是还是得刷一下的,主要是了解蓝桥杯的测评方法
然后刷题以“历届试题”为主,但是这份题不太全面,建议在 CSDN 上找别人的题解跟着练
我自己在准备蓝桥杯的时候也写了不少题解,可以看我的专栏:数据结构与算法专栏
力扣
网站链接:https://leetcode.cn/problemset/all
力扣的题型和蓝桥杯真题的题型很不一样 (主刷力扣 = 完蛋),但是力扣有很多的优点:
- 测评透明度高:哪个样例没通过可以看得清清楚楚,会提升你对特例的认知
- 性能排名:力扣会把你的代码性能和其它用户做比较,可以提升代码性能优化能力
- 题解全面:评论区有官方、民间题解,有多个解法的性能比较
我写的题集涉及到了较多的数据结构,这些在蓝桥杯测评系统、C 语言网是学不到的
有些题目比较简单,可以选择性地刷一些:LeetCode:算法面试题汇总
C 语言网
网站链接:https://www.dotcpp.com/oj/lanqiao/
C 语言网的题集收录了蓝桥杯的考试真题,而且比较全面,强力推荐
但是 C 语言网 Python 版本比较低 (3.8 以下),不支持 math 库的一些函数 (如 isqrt)
函数模板
考试是不能带模板的,而且绝大多数时候都是不能直接套用的 (需要根据题目微改),所以建议理解构造思路,自己多默写 (标 * 的表示重要性较低)
排列组合
字典序算法
以 [8, 3, 7, 6, 5, 4, 2, 1] 为例,这个函数完成的工作就是:
- 从右到左开始查找,因为 3 < 右边第一个数,所以记 3 的索引为 left
- 从右到左开始查找比 3 大的数,得到 4 的索引记为 right
- 交换 left 和 right 对应的数,此时序列变为 [8, 4, 7, 6, 5, 3, 2, 1]
- 可以看到 left 右侧全是逆序的 (即 4 的右侧),所以逆转 seq[left + 1: ] 得到 [8, 4, 1, 2, 3, 5, 6, 7]
def next_perm(seq):
""" 找到下个字典序
e.g.: 8 3 7 6 5 4 2 1
| | """
n = len(seq)
filt1 = lambda i: seq[i] >= seq[i + 1]
try:
l = next(it.dropwhile(filt1, range(n - 2, -1, -1)))
# 找到交换位
filt2 = lambda r: seq[l] >= seq[r]
r = next(it.dropwhile(filt2, range(n - 1, l, -1)))
seq[l], seq[r] = seq[r], seq[l]
# 逆转逆序区
seq[l + 1:] = seq[-1:l:-1]
return seq
except StopIteration:
return None数论
前 n 项平方和:
最小公倍数:
费马小定理: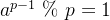
乘法逆元: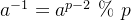
裴蜀定理:
大于 3 的质数可被表示成
质数筛法
网上比较推荐的算法是欧拉筛 (线性复杂度,无重复枚举) 和埃氏筛 (有重复枚举),但是在 Python 代码中,代码较为简单的埃氏筛有更高的效率
def prime_filter(n):
""" 质数筛选 (埃氏筛法)
:return: 质数标志
:example:
>>> is_prime = prime_filter(10000)
>>> sum(is_prime[2:])
1229"""
is_prime = [True] * (n + 1)
# 枚举 [2, sqrt(n)]
for i in filter(is_prime.__getitem__, range(2, math.isqrt(n) + 1)):
for c in range(i ** 2, n + 1, i):
is_prime[c] = False
return is_prime质因数分解
试除法是最基本的分解方法,在 Python 中 Pollard rho 算法对 7e5 以上的大数分解更快:大数的质因数分解 Python
def try_div(n):
""" 试除法分解"""
factor = {}
i, bound = 2, math.isqrt(n)
while i <= bound:
if n % i == 0:
# 计数 + 整除
cnt = 1
n //= i
while n % i == 0:
cnt += 1
n //= i
# 记录幂次, 更新边界
factor[i] = cnt
bound = math.isqrt(n)
i += 1
if n > 1: factor[n] = 1
return factor所有因数
def all_factor(n):
""" 所有因数"""
prime = try_div(n)
factor = [1]
for i in prime:
tmp = []
for p in map(i.__pow__, range(1, prime[i] + 1)):
tmp += [p * j for j in factor]
factor += tmp
return factor中国剩余定理 *
求满足以下条件的数 (其中 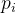
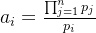
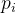
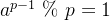
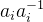
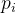
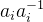
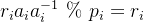
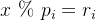
将每个余数单元乘以对应的余数累加起来,便可得到满足条件的数的余数项:
def rem_theorem(mods, rems, lcm_fcn=math.prod):
""" 中国剩余定理
:param mods: 模数集
:param rems: 余数集
:param lcm_fcn: 最小公倍数的求解函数 (模数集全为质数时使用 math.prod)
:return: lcm, 余数项"""
lcm = lcm_fcn(mods)
# 费马小定理求逆元, 要求 a,p 互质
inv = lambda a, p: pow(a, p - 2, p)
result = 0
for p, r in zip(mods, rems):
a = lcm // p
result += r * a * inv(a, p)
return lcm, result % lcm在用这个函数的时候一定要注意模数集的规模,因为是累乘所以数位会暴增,这会大幅度影响运行耗时
字符串
最长回文子串
Manacher 算法用于求解最长回文子串问题,但其中有个点比较难记忆,在此引用一个示例辅助
对于字符串 s="babba",先扩充为 s="^#b#a#b#b#a#$",并创建以下变量:
- 数组 p:以 p[i] 表示对应位置字符的“臂长”,s[i - p[i]: i + p[i] + 1] 范围内的字符串为回文串
- 指针 center, border:分别表示回文串的中心、右端点,总是表示最靠右的回文串
现给出两个示例,求解 p[10] 的初始值 (紫色格子),s 中的加深部分即为 center, border 所表示的回文串 (记为 sub)
因为回文串的对称性质,p[10] 可以根据 p[4] = 3 进行初始化:
- 示例 1:由于 10 + p[4] > border,所以 p[10] = min(p[4], border - 10)
- 示例 2:由于 10 + p[4] ≤ border,所以 p[10] = p[4],等价于 p[10] = min(p[4], border - 10)
得到 p[10] 的初始值之后,利用中心扩展法即可得到 p[10] 的最终值,结合 center, border 标记的更新即可写完 Manacher 算法
def manacher(s):
""" 最长回文子串"""
s = "#".join(s.join("^$"))
# 以对应字符为中心 最长回文串的半径
p = [0] * len(s)
center, border = 0, 0
for i in range(1, len(s) - 1):
# 利用回文串的对称性进行赋值, 利用 min 防止越界
p[i] = min(p[max(0, 2 * center - i)], max(0, border - i))
# 中心扩展法
while s[i - p[i] - 1] == s[i + p[i] + 1]: p[i] += 1
# 更新回文串中心, 回文串右端点 ("#")
if i + p[i] > border: center, border = i, i + p[i]
return max(p)图论
单源最短路
Dijkstra:使用额外的空间记录“单源最短路”,主体使用 while 循环
def dijkstra(src: int,
adj: Dict[int, Dict]):
""" 单源最短路径 (不带负权)
:param src: 源点
:param adj: 图的邻接表"""
n, undone = len(adj), [(0, src)]
# 单源最短路, 未访问标记
info = [[float("inf"), True] for _ in range(n)]
info[src][0] = 0
while undone:
# 找到离源点最近的点作为中间点 m
m = heapq.heappop(undone)[1]
if info[m][1]:
info[m][1] = False
# 更新单源最短路
for i in filter(lambda j: info[j][1], adj[m]):
tmp = info[m][0] + adj[m][i]
if info[i][0] > tmp:
info[i][0] = tmp
heapq.heappush(undone, (tmp, i))
return infoSPFA:使用额外的空间记录“单源最短路”、“顶点队列”、“在队标记”、“入队次数”,主体使用 while 循环 (队列非空)
def spfa(src: int,
adj: Dict[int, Dict]):
""" 单源最短路径 (带负权)
:param src: 源点
:param adj: 图的邻接表"""
n, undone = len(adj), [(0, src)]
# 单源最短路, 在队标记, 入队次数
info = [[float("inf"), False, 0] for _ in range(n)]
info[src][0] = 0
while undone:
# 队列: 弹出中间点
m = heapq.heappop(undone)[1]
info[m][1] = False
# 更新单源最短路
for i in adj[m]:
tmp = info[m][0] + adj[m][i]
if info[i][0] > tmp:
cnt = info[i][2]
# 入队: 被更新点
if not info[i][1]:
cnt += 1
heapq.heappush(undone, (tmp, i))
# 终止: 存在负环
if cnt > n: return None
info[i] = [tmp, True, cnt]
return info多源最短路
def floyd(adj: List[List]):
""" 多源最短路径 (带负权)
:param adj: 图的邻接矩阵"""
# import itertools as it
n = len(adj)
for m in range(n):
for i, j in it.combinations(it.chain(range(m), range(m + 1, n)), 2):
# 有向边写法
# adj[i][j] = min(adj[i][j], adj[i][m] + adj[m][j])
# adj[j][i] = min(adj[j][i], adj[j][m] + adj[m][i])
# 无向边写法
adj[i][j] = adj[j][i] = min(adj[i][j], adj[i][m] + adj[m][j])拓扑排序
def topo_sort(in_degree: List[int],
adj: Dict[int, Dict]):
""" AOV 网拓扑排序 (最小字典序)
:param in_degree: 入度表
:param adj: 图的邻接表"""
order = []
undone = [i for i, v in enumerate(in_degree) if v == 0]
heapq.heapify(undone)
while undone:
m = heapq.heappop(undone)
order.append(m)
# 删除该结点, 更新入度表
for i in adj[m]:
in_degree[i] -= 1
if in_degree[i] == 0: heapq.heappush(undone, i)
return order if len(order) == len(in_degree) else None最小生成树 *
def prim(src: int,
adj: Dict[int, Dict]):
""" 最小生成树
:param src: 源点
:param adj: 图的邻接表"""
n, edges = len(adj), []
# 未完成搜索的边
undone = [(v, i) for i, v in adj[src].items()]
heapq.heapify(undone)
# 和树的最小距离, 最近结点, 未完成标志
info = [[adj[src].get(i, float("inf")), src, True] for i in range(n)]
info[src][2] = False
while undone:
# 未被选取的顶点中, 离树最近的点
m = heapq.heappop(undone)[1]
if info[m][2]:
info[m][2] = False
edges.append((info[m][1], m))
# 更新最近结点
for i in adj[m]:
if info[i][0] > adj[m][i]:
info[i][:2] = adj[m][i], m
heapq.heappush(undone, (adj[m][i], i))
return edges并查集
目前我还没有遇见用并查集的题目,有备无患嘛:
- __init__:写入实例属性,_pre 为前驱结点列表 (初始均为自身),_rank 为结点级别
- find:查找某个结点的根结点
- is_same:检查两个结点是否属于同一棵树
- join:合并两个结点的根结点,根据根结点级别进行合并
- __repr__:规定并查集的字符串形式,调试时使用
class DisjointSet:
""" 并查集"""
def __init__(self, length):
# 记录前驱结点, 结点级别
self._pre = list(range(length))
self._rank = [1] * length
def find(self, i):
while self._pre[i] != i:
i = self._pre[i]
return i
def is_same(self, i, j):
return self.find(i) == self.find(j)
def join(self, i, j):
i, j = map(self.find, [i, j])
# 前驱不同, 需要合并
if i != j:
# 访问前驱级别
rank_i, rank_j = self._rank[i], self._rank[j]
# 前驱级别相同: 提高一个前驱的级别, 作为根结点
if rank_i == rank_j:
self._rank[i] += 1
self._pre[j] = i
# 前驱级别不同: 级别高的作为根结点
else:
self._pre[j] = i if rank_i > rank_j else j
def __repr__(self):
return str(self._pre)