目录
1 数字信号处理
数字信号处理:利用计算机或专用设备,以数值计算的方法对信号进行采集、变换、估值和识别等加工处理,借以达到提取信息和便于应用的目的。
信号:传递信息的函数,数学上表示为一个或多个自变量的函数。
- 连续时间信号:在连续的时间集合上有定义的信号;
- 模拟信号:时间连续,幅值连续;
- 离散时间信号:时间为离散变量的信号;
- 数字信号:时间离散,幅值离散。
2 离散时间信号
2.1 序列
离散时间信号的表示方法:序列表示法,函数表示法和图形表示法。
离散时间信号的基本运算:
- 移位:x(n-m)延时,x(n+m)超前;
- 反转/折叠:x(n)->x(-n);
- 序列求和与乘积{x(n)+y(n)},{x(n)*y(n)};
- 累加和计算:
- 尺度变换:x(n)->x(mn)抽取,x(n)=x(n/m)插值;
- 序列能量:归一化能量,表示信号在1欧姆电阻上产生的能量
2.2 离散时间信号
1. 单位取样序列
任意序列皆可以表示成各延迟单位取样序列的幅度加权和:
2. 单位阶跃序列
3. 矩形序列
4. 实指数序列
5. 正弦序列
其中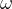
6. 复指数序列
,等幅震荡;
,实指数信号;
,
,直流信号。
7. 周期序列
3 离散时间系统
3.1 离散时间系统时域分析
3.1.1 线性非移变系统
线性系统:
非移变系统:
3.1.2 线性卷积
线性卷积(离散卷积):
即
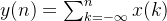
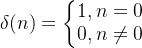

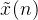
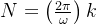
![T[x(n-k)]=y(n-k)](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT9UJTVCeCUyOG4tayUyOSU1RCUzRHklMjhuLWslMjk%3D)