贪心算法入门（一）

1.什么是贪心算法？

贪心算法是一种解决问题的策略，它将复杂的问题分解为若干个步骤，并在每一步都选择当前最优的解决方案，最终希望能得到全局最优解。这种策略的核心在于“最优”二字，意味着我们追求的是以最少的时间和精力，快速获得正确的结果。

然而，“希望得到全局最优解”就表示贪心算法并不意味着一定能得到全局最优解。实际上，并不是所有问题都可以通过贪心策略解决。为了确保贪心策略的有效性，需要对其进行严格的证明。而且，不同的问题往往需要采用不同的贪心策略。

如果你觉得这一点仍然比较抽象，接下来我将通过五道具体的例题来详细说明贪心算法的应用及其背后的思路。

2.柠檬水找零

通过示例和问题描述，理解这个问题并不难，所以我就不过多阐述了。就是看能不能给bills数组里面的每个顾客正确的找零，并且一开始我们手上是没有零钱的，也就意味着如果bills[0] > 5, 那么我们是没有办法给顾客找零的，因为此时我们还没有任何零钱。以此类推，当检索完整个数组都能正确找零时返回true，否则返回false。

在理清问题后，不要急于去想出一个贪心策略，也不要急于去想用代码如何实现。而是首先在你脑子里面去想示例里面的答案是如何一步一步得到的。

示例1中，第1位顾客用5美元买柠檬水，不用找零，与此同时我们手上多了一张5元的零钱。以此类推，直到第4位顾客付了10美元，我们需要找零5美元，此时我们的零钱库中有3张5美元，可以正确找零，此时零钱库变为2张5美元，1张10美元。最后一位顾客，我们只需找1张10美元和1张5美元，故可以实现正确找零，返回true。

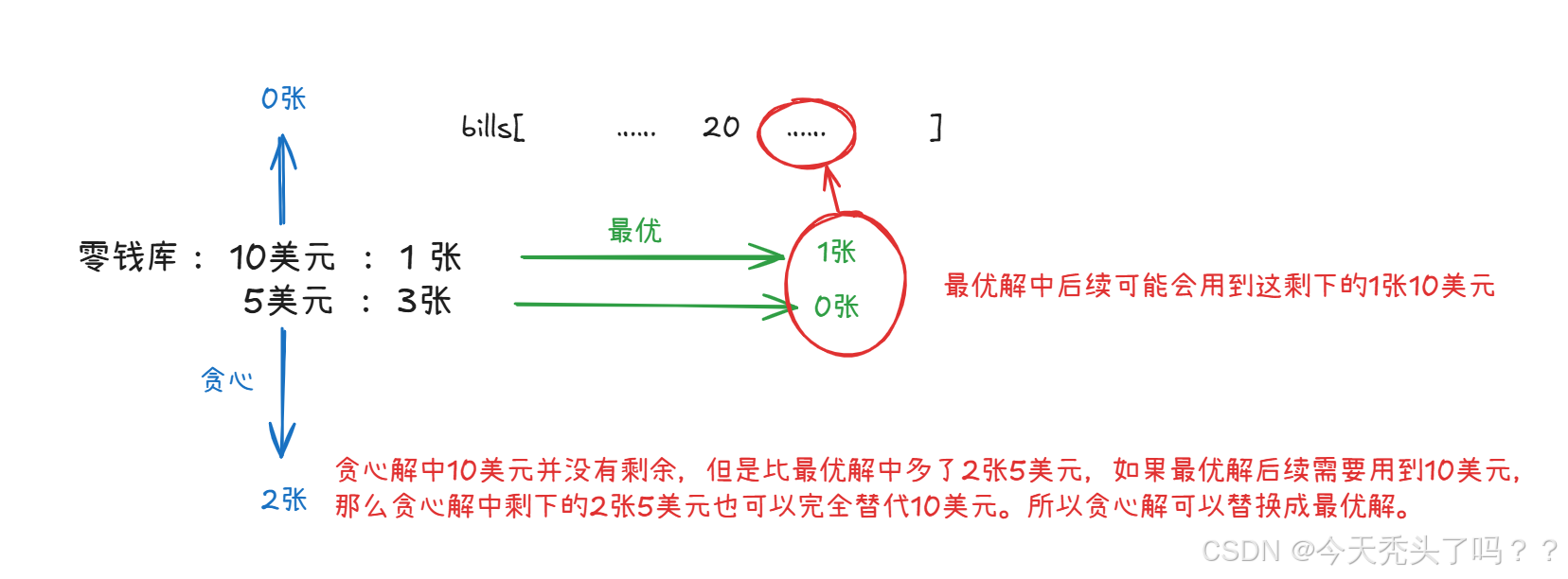
再把以上思路，变现为代码即可。但其实还有一个细节问题需要我们考虑，就是如果顾客支付20元，而此时我们的零钱库中有3张5美元和1张10美元，那么我们应该选择3张5美元还是1张10美元1张5美元进行找补呢？这时可能会想到用递归的方式将两种方式递归下去，只要有一种的结果为true那么就为true。但同时递归这种方式时间复杂度就会大大提升。此时能不能有一种贪心策略去简化呢？

3张5美元和1张10美元1张5美元，应该更优先选择1张10美元1张5美元进行找补。这就是我们贪心的地方，因为5美元的用处比10美元更大，当顾客支付10美元时，5美元可以找补，同时5美元也可以为20找补。所以我们应该留着用处更大的5美元，以备不时之需。

那么这种策略对不对呢，这个贪心策略得到的结果是不是正确的，需要证明。我们可以反推假设，假设在最优解中，我们在某一次找补20美元的选择中，并没有选择1张10美元和1张5美元，而是选择了3张5美元。而我们的贪心策略是要选择1张10美元和1张5美元的，我们把贪心的选择往假设的最优解中进行替换，看是否会影响后续结果。

代码实现

class Solution {
    public boolean lemonadeChange(int[] bills) {
        int five = 0, ten = 0; // five表示零钱库中5美元的张数，ten表示10美元的张数
        for(int i = 0; i < bills.length; i++){ 
            if(bills[i] == 5) five++; // 更新零钱库
            else if(bills[i] == 10){
                if(five == 0) return false; // 如果零钱库没有5美元返回false
                five--;ten++; // 更新零钱库
            }
            else{
                if(ten > 0 && five > 0) {ten--;five--;} // 优先选择用10美元和5美元找补
                else if(five >= 3) five -= 3; // 次选3张5美元（在没有10美元的情况下）
                else return false; // 上述条件都不满足则没有合适的零钱找补返回false
            }
        }
        return true;
    }
}

3. 将数组和减半的最少操作次数

2208. 将数组和减半的最少操作次数 - 力扣（LeetCode）

这道题的贪心策略并不难想，要让操作次数最少，只需每次都挑出数组最大的数进行减半，但是需要注意的是，减半后的数也需要放回原数组，然后挑出最大值。所以不能直接将数组用sort方法进行排序，因为还需要将减半后的数重新放回数组进行比较。采取使用大根堆的数据结构即可。

代码实现

class Solution {
    public int halveArray(int[] nums) {
        PriorityQueue<Double> q = new PriorityQueue<>((a, b) -> Double.compare(b, a));
        int ret = 0;
        double sum = 0;
        for(int x : nums){sum += x;q.add((double) x);} // 原数组总和
        sum /= 2.0; // 计算总和的一半
        while(sum > 0){
            double t = q.poll() / 2.0; // 拿出堆中最大的数
            sum -= t;
            ret++;
            q.offer(t);// 减半后的数重新放回大根堆
        }
        return ret;
    }
}

4.最大数

179. 最大数 - 力扣（LeetCode）

以示例1为例，10和2我们很容易看出来，应该让2在高位，10放在2后面。所以实现的逻辑就是，把两个数从高位到低位的数字挨个比较，直至数字不同，并把数字大的放在前面。比如10和2的比较逻辑就是，10的第一位数字1和2比较，2比1大所以放前面。再比如23和22, 23的第一位是2,22的第一位也是2，所以继续向后比较就3和2比较，所以23和22组成的最大值应该是2322。

但还存在一种情况就是，2和20，这种情况应该把谁放在前面呢，肉眼观察最大值应该是220，所以应该把2放前面20放后面。但是这个结论我们应该用逻辑推敲出来而不是凭空想。难道遇到这种情况就是把位数少的放前面吗？那2和24就显然不是这种情况，因为224比242要小。但是从这两个例子就可以看出端倪了，如果多出的数字比首位大那么就是位数多的排前面，否则排后面。2和20中0比2小，所以20应该排在后面，而2和24中4比2大，所以24应该排前面。

所以我们只要按照这种方法对数组进行降序排序，再依次遍历数组就可以得到最终结果值。其实还有一种更简单的比较方法，就是将数a和数b都转换为字符串，然后比较 a + b（a在前，b在后）大还是（b + a）大即可。

代码实现

class Solution {
    public String largestNumber(int[] nums) {
        String[] s = new String[nums.length];
        for(int i = 0; i < nums.length; i++) s[i] = "" + nums[i]; // 将数转换为字符串存入字符数组
        Arrays.sort(s, (a, b) -> (b + a).compareTo(a + b)); // 按照比较方法对字符数组进行降序排序
        if(Objects.equals(s[0],"0")) return "0"; // 判断特殊情况，如果排序后的最大值是0就返回0
        StringBuilder ret = new StringBuilder();
        for(String t : s) ret.append(t); // 依次添加
        return ret.toString();
    }
}

5.摆动序列

376. 摆动序列 - 力扣（LeetCode）

摆动序列其实就是一种波浪型曲线，要你找的这个子序列必须是先升再降再升再...,或者先降再升再降...。而且子序列就表示中间可以不用是连续的，也就表明你可以在数组里面跳着挑满足摆动的数。最终找出最长的子序列即可。

我先说一下我一开始看到这道题的思路，就是用动态规划。但其实这道题用贪心的思路是更简单的，但是动态规划和贪心的时间复杂度是一样的。我在力扣上跑的结果所花的时间也是差不多的。只是贪心的逻辑会更简单，但是贪心的策略是比较扩散性思维才能想到的，但是也不难。这里想讲一下动态规划的思路是因为是比较容易想和常规的。如果想直接看贪心策略的可以直接跳到贪心的思路。

动态规划思路：

首先明确状态表示，最开始想的是dp[i]表示以i位置为结尾的摆动最长子序列长度，但是很快被否定了，因为这样我没有办法写状态转移方程，因为我不知道以i位置结尾的是上升趋势还是下降趋势，就没有办法知道后续那个数可以加在这个状态之上。所以用两个数组表示不同的状态。

 int[] f = new int[n]; // 以i结尾并且为上升趋势的摆动序列最长长度
 int[] g = new int[n]; // 以i结尾并且为下降趋势的摆动序列最长长度

当nums[ j ] < nums[ i ] （j 表示在 i 之前的所有索引值），为上升趋势，所以应该连上为下降趋势的序列组成新的摆动序列，即更新 f[ i ] = g[ i ] + 1, 当nums[ j ] > nums[ i ] 时，更新g[ i ] = f[ i ] + 1。需要注意的是在更新i位置的值时，需要把i之前的所有的f[ j ] 和 g[ j ]都遍历比较一遍，看接在哪个位置后才能组成最长的摆动子序列。还有就是初始值问题，每个数自己也能单独组成摆渡序列，所以f [ i ] 和 g [ i ] 的初始值都应该为1。

动规代码实现：

class Solution {
    public int wiggleMaxLength(int[] nums) {
        int n = nums.length;
        int[] f = new int[n]; // 以i结尾并且为上升趋势
        int[] g = new int[n]; // 以i结尾并且为下降趋势
        for(int i = 0; i < n; i++) f[i] = g[i] = 1;
        int ret = 1;
        for(int i = 1; i < n; i++){
            for(int j = 0; j < i; j++){
                if(nums[j] > nums[i]) g[i] = Math.max(g[i], f[j] + 1);
                if(nums[j] < nums[i]) f[i] = Math.max(f[i], g[j] + 1);
            }
            ret = Math.max(ret, Math.max(f[i], g[i]));
        }
        return  ret;
    }
}

以上实现思路时间复杂度为n², 因为多了一个找出最合适j位置的循环。所以我的优化思路就是想把这个寻找j位置的循环省掉。如果我的f 和 g函数表示在0 - i区间内最长摆动子序列的值，我就不用去找j位置了，直接用这个值往上加即可。但是这样的话我的判断条件又会缺少值，因为不知道最长子序列的最后一位数是什么，就没有办法判断哪些数可以接在后面，所以又新开一个二维数组hash，hash[i][0]表示在0-i区间内最长摆动序列且结尾为下降趋势的最后一位数的值，hash[i][1]表示在0-i区间内最长摆动序列且结尾为上升趋势的最后一位数的值。

所以条件判断变成了，nums[ i ] 和 hash [ i - 1] [ 0 ] 、 hash [ i - 1] [ 1 ] 进行比较，如果nums[ i ] > hash [ i - 1] [ 0 ], 表示当前位置的值大于在0 - i - 1区间内结尾为下降趋势的最长摆动序列的最后一位数，满足条件则更新f[ i ] 的值，并且hash [ i ] [ 1 ] 也要更新为当前数。

f[i] = g[i - 1] + 1; hash[i][1] = nums[i];

如果不满足,f[ i ] 的值应该延续 f[ i - 1] 的值，并且hash [ i ] [ 1 ] 也应该延续hash [ i - 1] [ 1 ] 的值。

g[i]同理。

优化后的代码：

class Solution {
    public int wiggleMaxLength(int[] nums) {
        int n = nums.length;
        int[] f = new int[n]; // 在0-i区间内 结尾为上升趋势
        int[] g = new int[n]; // 在0-i区间内 结尾并且为下降趋势
        for(int i = 0; i < n; i++) f[i] = g[i] = 1;
        int[][] hash = new int[n][2];
        hash[0][0] = hash[0][1] = nums[0];
        for(int i = 1; i < n; i++){
           if(nums[i] > hash[i - 1][0]) { f[i] = g[i - 1] + 1; hash[i][1] = nums[i]; }
           else { f[i] = f[i - 1];  hash[i][1] = hash[i - 1][1];}
           if(nums[i] < hash[i - 1][1]) { g[i] = f[i - 1] + 1; hash[i][0] = nums[i]; }
           else { g[i] = g[i - 1];  hash[i][0] = hash[i - 1][0];}
        }
        return  Math.max(f[n -1], g[n - 1]);
    } 
}

贪心思路：

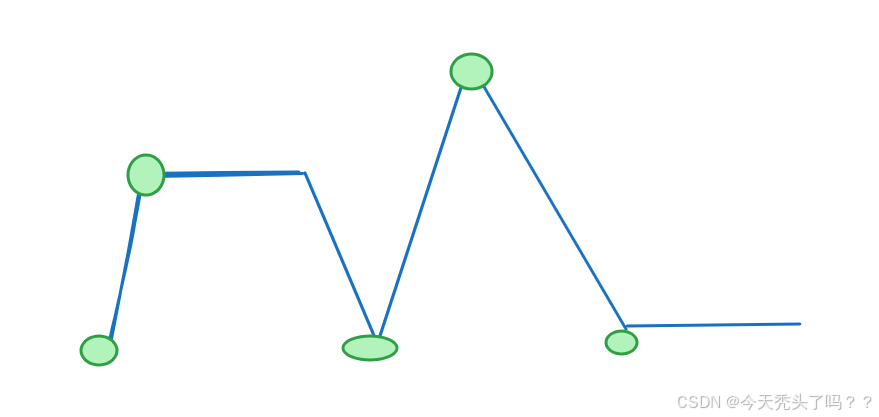
把数组用折线表示，下图是我随便画的一种情况，你可以随便用折线画你假设的数组，从图中可以看出我们要要找的摆动序列长度的最大值就是一共有多少个拐点，但是连续的相同拐点只能算一个。这些拐点也叫极点，判断是不是极点的方式：该点和左区间值的差值left和和右区间的差值right相乘是否小于0，小于0则为极点，大于0说明一直都是上升趋势或下降趋势，等于0则说明是连续相等的区间。

贪心代码实现

class Solution {
    public int wiggleMaxLength(int[] nums) {
        int n = nums.length;
        if (n < 2) return n;
        
        int ret = 0, left = 0, right = 0;
        for(int i = 0; i < n - 1; i++){ // 注意没有考虑最后一个
            right = nums[i + 1] - nums[i]; 
            if(right == 0) continue; // 先将右区间更新到拐点位置
            if(right * left <= 0) ret++; // 条件中等于0是为了第一次循环左区间为0的特殊情况
            left = right;
        }
        return ret + 1; // 要加上最后一个位置，因为最后一个位置必为极点
    }
}

6.最长递增子序列

300. 最长递增子序列 - 力扣（LeetCode）

这道题依然会讲解动态规划和贪心两种方法思路，再在动态规划的基础上去优化得到贪心。

动态规划思路：

dp[ i ] 表示以i位置为结尾的最长递增子序列，状态转移方程为j < i && nums[ j ] < nums[ i ] ,dp [ i ] = max( dp [ j ] + 1) 。

动态规划代码实现

class Solution {
    public int lengthOfLIS(int[] nums) {
        int n = nums.length;
        int[] dp = new int[n]; // 表示以dp[i]位置结尾的最长递增子序列长度
        Arrays.fill(dp,1);
        int ret = 1;
        for(int i = 1; i < n; i++){
            for(int j = 0; j < i; j++){
                if(nums[i] > nums[j]) dp[i] = Math.max(dp[i], dp[j] + 1); // 满足条件表示i位置的值可以跟在j位置后形成递增序列
            }
            ret = Math.max(ret, dp[i]); // 更新最大值
        }
        return ret;
    }
}

时间复杂度是n²。因为多了找最合适的j位置的循环，需要想办法把这个循环省掉。根据上一题给的思路，依然可以把状态表示dp[ i ] 重新定义为在0 - i区间的最长递增子序列长度。但是依然需要考虑判断条件是跟谁比较，由于这里定义为区间内并不知道结尾的数是多少，所以新开一个数组key[i]表示在0 - i区间内最长递增子序列的最后一个数。看似很合理但是实际上状态转移方程还是写不出来的。

key[0] = nums[0];
        for(int i = 1; i < n; i++){
           if(nums[i] > key[i - 1]) { dp[i] = dp[i - 1] + 1; key[i] = nums[i]; }
           else (nums[i] < key[i - 1]) { dp[i] = dp[i - 1]; key[i] = key[i - 1]; }
        }

nums[ i ] > key[i - 1] 这种情况是可以正确写出状态转移方程的，只需在上一个区间的最长序列长度加1即可，并且更新结尾值为当前i位置的值。但如果是小于的情况，dp[ i ] = dp[ i - 1]继续延续上一个区间的状态没错，可是 key[ i ] 的值却不能简单的用延续处理。例如数组为【10， 1 ，3】这种情况，当i = 1 的时候如果简单的把key[ i ] 的值延续上一次的状态为10，那么最终肯定是不能得到正确答案长度为2的序列1,3的。那么key[ i ] 的值在这种情况下应该怎么更新呢？你会发现需要处理很多种情况，并且只记录递增子序列最后的数根本不能应对这些情况，因为有可能最长递增子序列需要以另外一个位置为起点开头，或者说在中间把一些点替换掉。例如【9,10,1,2,3】，【1,2,11,12,5,6,7】。

贪心思路

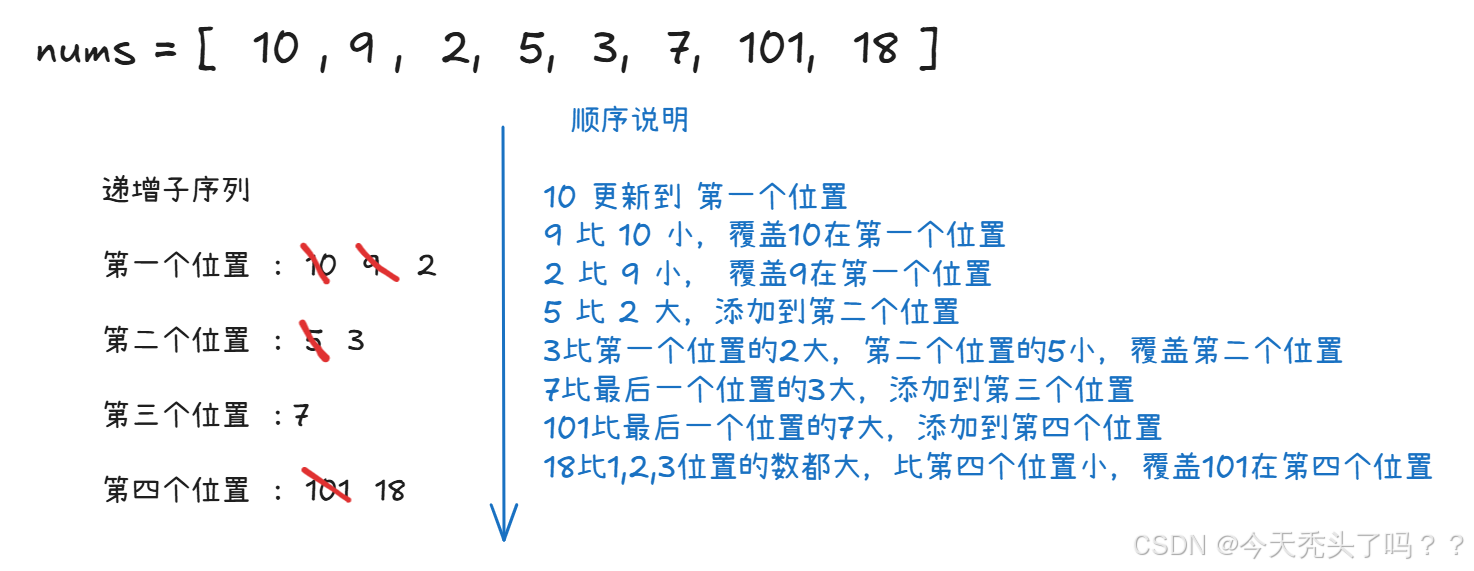
贪心策略就是在以上思路发散扩展得来的。以示例1为例：

从左至右扫描数组，10可以看成一个单独的递增序列，长度为1。再扫描到9, 9 比 10 小，此时也能单独看成长度为1的递增序列。这时我们把10这个单独递增序列剔除掉，保留9的序列。因为在长度同样的情况下，保留越小的数，能够加在该数后形成递增的情况越多。扫描到2同理，保留2的单独序列，扫描到5，比2大，直接让长度加1，扫描到3，比2大比5小，此时可以把最长递增序列的第二位换成3，最长长度依然为2。以此类推。

通过扫描数组不断地更新每个位置的数，和添加新位置，最终得到最长递增子序列长度。

添加位置的时机：只要比最后一个位置的数大就添加位置。

更新某个位置的时机：从第一个位置依次往后比较，找到一个小于等于该数的位置，在该位置更新，更新的值为当前扫描的数。

贪心代码实现

class Solution {
    public int lengthOfLIS(int[] nums) {
        List<Integer> list = new ArrayList<>();
        for(int x : nums){
            if(list.size() == 0) list.add(x); // 第一个数直接放入list
            else{
                if(x > list.get(list.size() - 1)) list.add(x); // 如果大于最后一个位置，直接添加放到新位置
                else{ // 否则从第一个位置开始依次比较找到放入的位置
                    for(int i = 0; i < list.size(); i++){
                        if(x <= list.get(i)) { list.set(i,x); break;} // 找到第一个小于等于的位置更新该位置的值
                    }
                }
            }
        }
        return list.size();// list的大小表示在过程中最多添加了多少位置
    }
}

优化：
在更新某个位置的数时，可以使用二分查找，快速找到该位置进行更新。需要注意的是，找出的位置是严格大于上个位置的数的，在更新left和right的时候需要注意这个细节。

class Solution {
    public int lengthOfLIS(int[] nums) {
        List<Integer> list = new ArrayList<>();
        for(int x : nums){
            if(list.size() == 0) list.add(x);
            else{
                if(x > list.get(list.size() - 1)) list.add(x);
                else{
                    int left = 0, right = list.size() - 1, mid = (left + right) / 2;
                    while(left < right){
                        if(x > list.get(mid)) left = mid + 1;
                        else if(x < list.get(mid)) right = mid;
                        else break;
                        mid = (left + right) / 2;
                    }
                    list.set(mid,x);
                }
            }
        }
        return list.size();
    }
}

结语

欢迎大家在评论区讨论留言，有不理解的地方可以私信或者评论。