深度优先遍历——Depth First Search是图论中非常重要的算法之一。

应用场合：拓扑排序、走迷宫、搜索引擎、爬虫等。

图是什么？

1.图是一种逻辑结构，由有限个顶点与边连接组成；

2.图中，点与点之间的边不存在顺序关系，即是无序的；

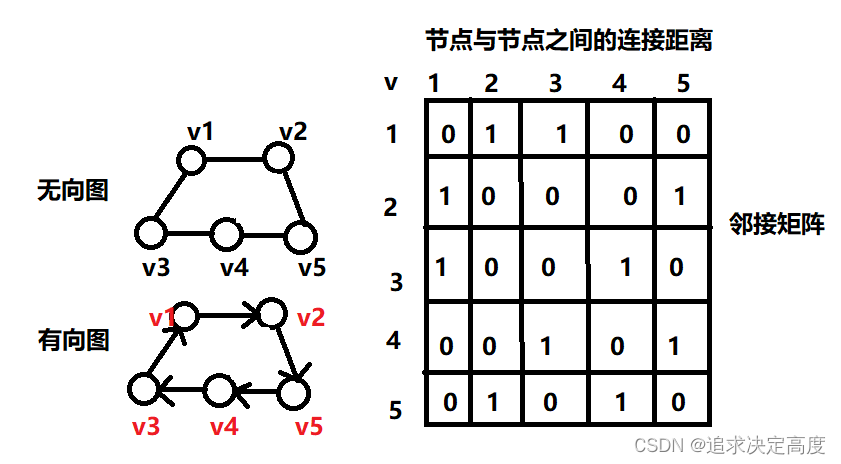
3.图可以用邻接矩阵实现顺序存储，也可以通过邻接表来实现链式存储。

其中，图可以分为有向图与无向图：

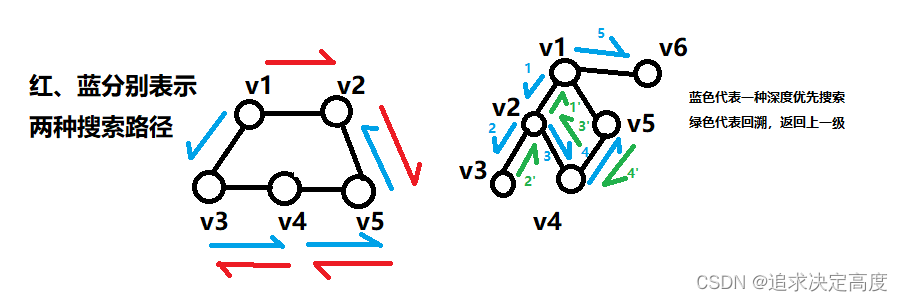
深度优先搜索搜索路径为：

 由上图可知，深度优先搜索就是一条路走到黑，如果走到头了，将通过一遍又一遍的返回上级，来寻找另一种可以走通的路，继续走到黑，如此反复，直到全部遍历完结点为止。

注意：在图的遍历过程中，需要额外创建一个数组，如果已经遍历该结点，则在数组中将该节点的位置标志1，用来说明这个结点已经访问过，不能再作为寻路方案。

如果已经走到头了，回溯【返回上一级】时，将该节点置位0，以便于其他的寻路方案可以经过该节点。

深度优先搜索的代码实现：

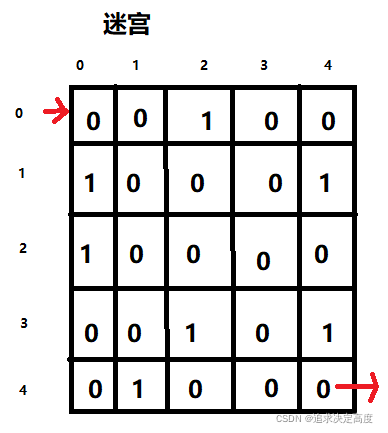
输入一个5*5的迷宫，其中1表示障碍，0表示此路可走，利用DFS实现起点到终点的寻路方案，求出方案总数 以及 最短方案步数。

#include<iostream>

using namespace std;

int startx,starty;//定义起点坐标
int endx ,endy;//定义终点坐标
int step=0;//定义一个步长，用来判断最短距离
int num=0;//用来记录方案总数
int minstep=99999;//用来更新最小值
int isWalked[10][10];//定义一个检查是否走过的数组，内部元素默认为0
int a[5][5];//定义 一个5行5列的数组 存放迷宫
//定义四个寻路方向，用两个一维数组表示
int dx[]={0,0,1,-1};
int dy[]={1,-1,0,0};

//3.深搜
void dfs(int x,int y, int step)
{
    //深度优先遍历用递归，所以确定了返回值和参数后，需要确定判断终止条件
    if(x==endx&&y==endy)//如果传入的 x,y 为终点坐标，表示已经找到了一种方案
    {
        num++;//找到了方案就加
        if(step<minstep)//如果当前到达终点的步长小于最短距离，此时该步长为最短距离
        {
            minstep=step;
        }
        return; //结束
    }
    
    for(int k=0;k<4;k++)//表示四种寻路方向
    {
//表示下一步需要经过的结点
        int tx=x+dx[k];
        int ty=y+dy[k];
        if(tx<0||ty<0||tx>4||ty>4||a[tx][ty]==1||isWalked[tx][ty]==1)//边界条件
            continue;
        isWalked[tx][ty]=1;//走过该节点，将该节点置位1
        dfs(tx,ty,step+1);//把当前节点做递归，回到判断是否到达终点，如果到达终点就进行回溯
        isWalked[tx][ty]=0;//回溯时，将该点置位0；
    }
      return;//结束
}
int main()
{
      // 1. 输入迷宫
    for(int i=0;i<5;i++)
    { 
        for(int j=0;j<5;j++)
        {
            cin>>a[i][j];
        }
    }
      //2.输入起点与终点
    cin>>startx>>starty>>endx>>endy;
    isWalked[startx][starty]=1;//从起点开始出发，所以起点先置位1
    dfs(startx,starty,step);//将起始点引入深度优先搜索函数中，此时最短距离为0

    cout<<minstep<<endl;
    cout<<num<<endl;

    return 0;
}