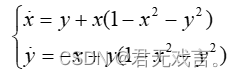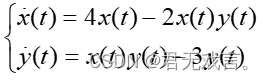| 一、实验目的: 理解并掌握利用MATLAB绘制生物数学相关方程中的解曲线。 |
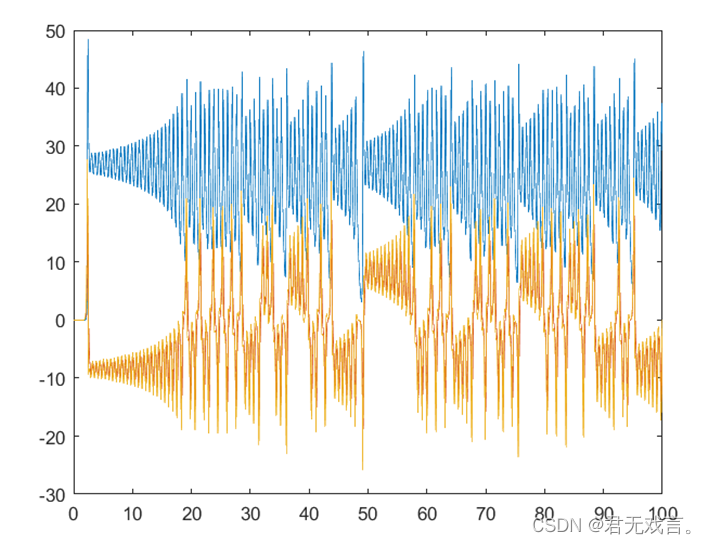
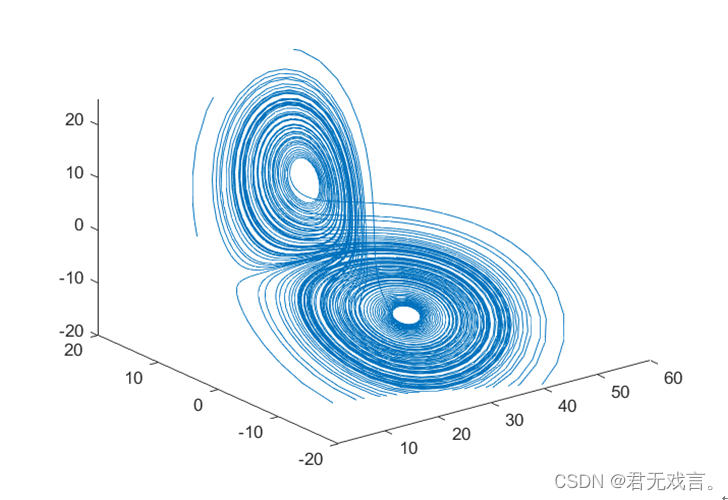
| 二、实验内容 例 著名的Lorenz模型的状态方程表示如下
其中,设 练习 (选做两个) 1、极限环是二阶非线性常微分方程中一种常见现象,对某些非线性微分方程来说,不论初始状态为何值,微分方程的相轨迹都将稳定在一条封闭的曲线上,该曲线称为微分方程的极限环。试取初值,绘制出微分方程
的极限环,并将plot函数换成comet函数,观察绘制动画式轨迹的过程。 2、Lotka-Volterra捕食模型方程为
初值为 3、画出《生物数学原理》50页图3.2.5中两种情况。 4、画出《生物数学原理》54、55页的三个图(按所给参数去验证)。 |
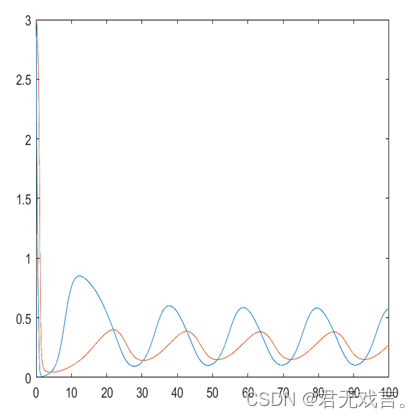
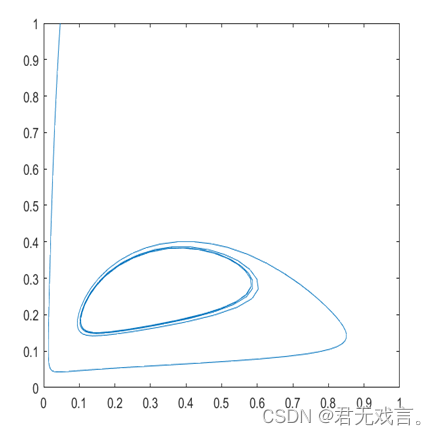
| 程序代码: 例1 f=@(t,x)[-8/3*x(1)+x(2)*x(3);-10*x(2)+10*x(3);-x(1)*x(2)+28*x(2)-x(3)]; t_final=100;x0=[0;0;1e-10]; [t,x]=ode45(f,[0,t_final],x0);plot(t,x),figure; plot3(x(:,1),x(:,2),x(:,3)); axis([1 60 -20 20 -20 25]); 练习1. f=@(t,x)[x(2)+x(1)*(1-x(1)^2-x(2)^2);-x(1)+x(2)*(1-x(1)^2-x(2)^2)]; t_final=100;x0=[0;1e-10]; [t,x]=ode45(f,[0,t_final],x0);plot(t,x),figure; plot(x(:,1),x(:,2)); axis([-1 1 -1 1]) 练习3. a=1 b=0.3 d=0.1 f=@(t,x)[x(1)*(1-x(1))-a*x(1)*x(2)/(x(1)+d);b*x(2)*(1-x(2)/x(1))] t_final=100;x0=[3,3]; [t,x]=ode45(f,[0,t_final],x0);plot(t,x),figure; plot(x(:,1),x(:,2)); axis([0 1 0 1]) clear;clc a=1 b=0.2 d=0.1 f=@(t,x)[x(1)*(1-x(1))-a*x(1)*x(2)/(x(1)+d);b*x(2)*(1-x(2)/x(1))] t_final=100;x0=[3,3]; [t,x]=ode45(f,[0,t_final],x0);plot(t,x),figure; plot(x(:,1),x(:,2)); axis([0 1 0 1]) |
| 例1. |
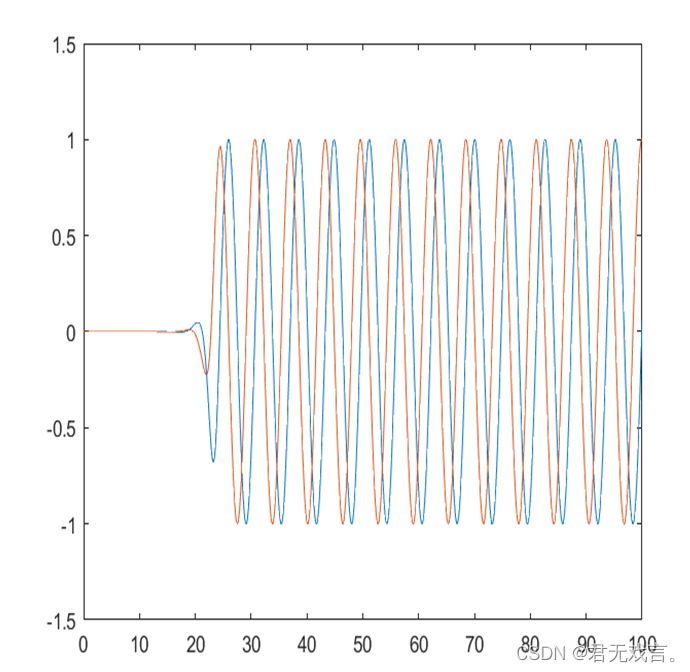
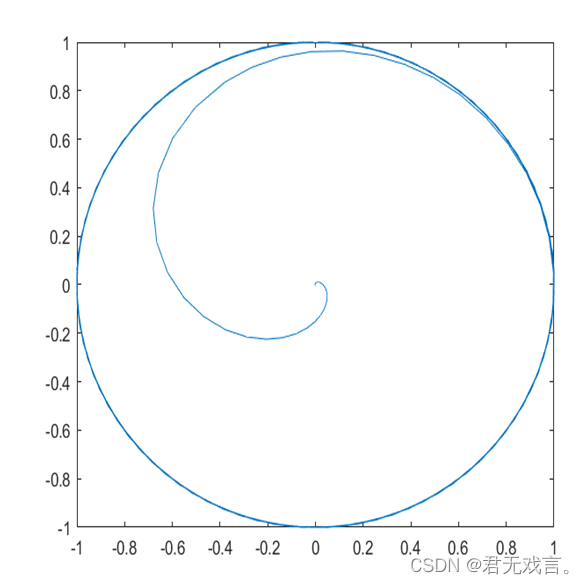
| 练习1.
|
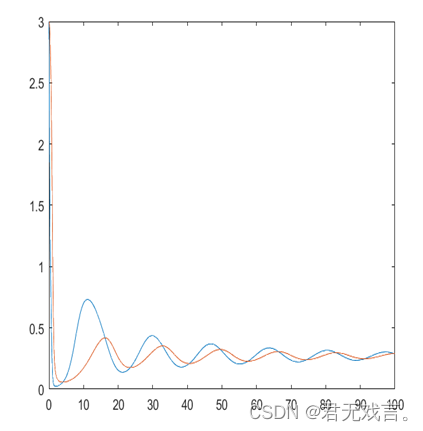
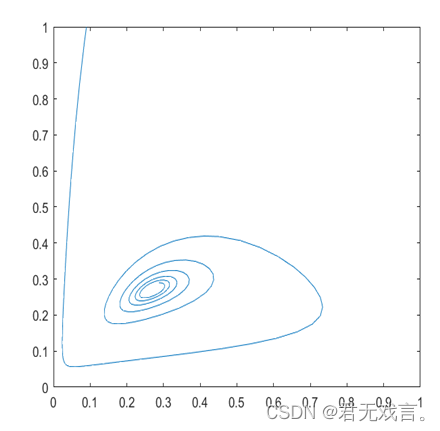
| 练习3. a = 1 b = 0.300000000000000 d = 0.100000000000000 f = 包含以下值的 function_handle: @(t,x)[x(1)*(1-x(1))-a*x(1)*x(2)/(x(1)+d);b*x(2)*(1-x(2)/x(1))]
a = 1 b = 0.200000000000000 d = 0.100000000000000 f = 包含以下值的 function_handle: @(t,x)[x(1)*(1-x(1))-a*x(1)*x(2)/(x(1)+d);b*x(2)*(1-x(2)/x(1))] |
| 分析与讨论:
|
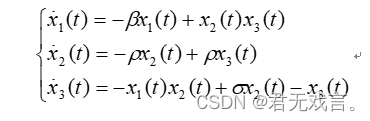
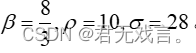 。若令其初值为
。若令其初值为