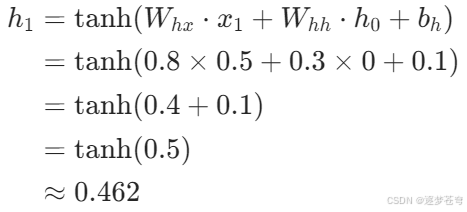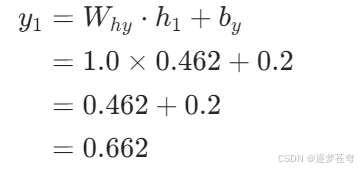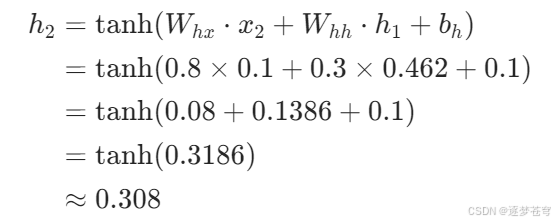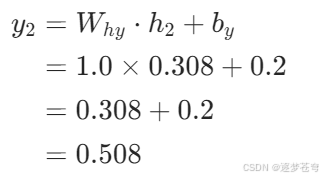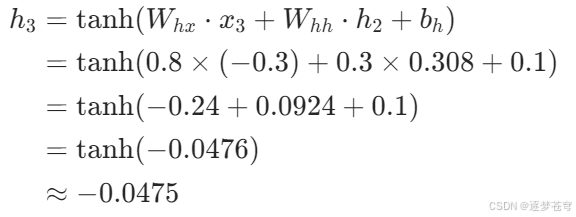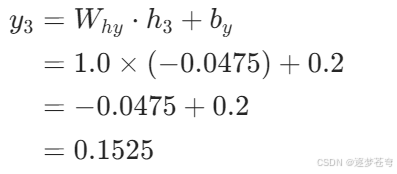文章目录
🍃作者介绍:双非本科大三网络工程专业在读,阿里云专家博主,专注于Java领域学习,擅长web应用开发、数据结构和算法,初步涉猎人工智能和前端开发。
🦅个人主页:@逐梦苍穹
📕所属专栏:人工智能
🌻gitee地址:xzl的人工智能代码仓库
✈ 您的一键三连,是我创作的最大动力🌹
1、学习介绍
循环神经网络(Recurrent Neural Networks, RNNs)是一类用于处理序列数据的神经网络模型。
它们在处理诸如时间序列分析、自然语言处理和语音识别等任务时表现出色。
RNN的核心特性是它们能够在序列中保存状态信息,从而捕捉输入序列中的时间依赖关系。
在循环神经网络的这部分,后续的文章主要包含内容如下:
- 了解词嵌入层的作用
- 了解循环网络层的作用
- 穿插各种数学原理和python代码
最后,将会有一篇文章来使用前面学习的知识来构建一个 循环神经网络,实现对歌词数据的学习,并能够根据给出的词来预测出指定长度的歌词。
2、RNN的基本结构
RNN与传统的前馈神经网络(文末讲解)不同,它的每个神经元 不仅 接收来自 输入层的信号,还接收来自 自身或其他神经元的反馈信号。
这种反馈机制使RNN能够在处理序列数据时保留之前的信息,从而在时间步之间共享信息。
2.1、图例
这张图展示了一个典型的循环神经网络(RNN)结构,以及它在时间步上的展开(unfolding)
图中元素的解释:
- 输入层(input):
- 标记为 x x x(单个时间步的输入)。
- 在展开的图中,每个时间步 t t t 的输入标记为 x t x_t xt。
- 隐藏层(hidden):
- 标记为 s s s(表示隐藏状态)。
- 图中,隐藏层的状态在每个时间步用 s t s_t st 表示。隐藏层保存了当前输入和之前隐藏状态的信息。
- 权重 W W W 用于在时间步之间传播隐藏状态。
- 输出层(output):
- 标记为 o o o。
- 在展开的图中,每个时间步的输出标记为 o t o_t ot。
- 权重 V V V 用于将隐藏状态转换为输出。
- 权重矩阵:
- U U U:输入到隐藏层的权重矩阵。
- W W W:隐藏层之间的循环权重矩阵,用于将先前的隐藏状态 s t − 1 s_{t-1} st−1 传播到当前时间步的隐藏状态。
- V V V:隐藏层到输出层的权重矩阵。
2.2、公式
在RNN中,隐藏状态 h t h_t ht 的更新公式为: h t = f ( W h x x t + W h h h t − 1 + b h ) h_t = f(W_{hx} x_t + W_{hh} h_{t-1} + b_h) ht=f(Whxxt+Whhht−1+bh)
- h t h_t ht 是时间步 t t t 的隐藏状态。
- x t x_t xt 是时间步 t t t 的输入。
- W h x W_{hx} Whx 是输入到隐藏层的权重矩阵。
- W h h W_{hh} Whh 是隐藏层到隐藏层的权重矩阵。
- b h b_h bh 是偏置项。
- f f f 是激活函数,通常使用 tanh \tanh tanh 或 ReLU \text{ReLU} ReLU。
输出 y t y_t yt 通常由以下公式给出: y t = f ( W h y h t + b y ) y_t = f(W_{hy} h_t + b_y) yt=f(Whyht+by)
- W h y W_{hy} Why 是隐藏层到输出层的权重矩阵。
- b y b_y by 是输出层的偏置项。
所以实际上RNN就是
x
t
x_t
xt 和
h
t
−
1
h_{t-1}
ht−1线性组合后,通过tanh函数向前传递。
2.3、公式计算示例
一个简单的RNN计算示例,通过给定的输入序列、初始状态和权重矩阵,演示如何计算每个时间步的隐藏状态和输出。
2.3.1、给定参数
- 输入序列: x = [ 0.5 , 0.1 , − 0.3 ] x = [0.5, 0.1, -0.3] x=[0.5,0.1,−0.3]
- 初始隐藏状态: h 0 = 0 h_0 = 0 h0=0
- 权重矩阵:
- W h x = 0.8 W_{hx} = 0.8 Whx=0.8
- W h h = 0.3 W_{hh} = 0.3 Whh=0.3
- W h y = 1.0 W_{hy} = 1.0 Why=1.0
- 偏置项:
- b h = 0.1 b_h = 0.1 bh=0.1
- b y = 0.2 b_y = 0.2 by=0.2
- 激活函数:使用 tanh \tanh tanh,其定义为 tanh ( z ) = e z − e − z e z + e − z \tanh(z) = \frac{e^z - e^{-z}}{e^z + e^{-z}} tanh(z)=ez+e−zez−e−z
2.3.2、时间步计算
时间步 1 (
t
=
1
t = 1
t=1):
输入:
x
1
=
0.5
x_1 = 0.5
x1=0.5
-
隐藏状态计算:
-
输出计算:
时间步 2 (
t
=
2
t = 2
t=2):
输入:
x
2
=
0.1
x_2 = 0.1
x2=0.1
-
隐藏状态计算:
-
输出计算:
时间步 3(
t
=
3
t = 3
t=3):
输入:
x
3
=
−
0.3
x_3 = -0.3
x3=−0.3
-
隐藏状态计算:
-
输出计算:
通过这几个时间步的计算,我们可以看到 RNN如何利用之前的隐藏状态和当前的输入来计算当前的隐藏状态,并进一步生成输出
3、序列依赖与梯度消失/爆炸
3.1、序列依赖
概念:
- 序列依赖指的是序列数据中元素之间的相互关系和依赖性。
- 在时间序列、自然语言处理、语音识别等任务中,当前数据点通常与之前的若干数据点相关联。
- RNN 利用其循环结构来捕获序列中的时间依赖性。通过记住和传递过去的隐藏状态,RNN 可以将过去的信息带入到当前的计算中。
例子:
- 自然语言处理:在句子中,当前词的含义通常取决于前面的词。例如,“我喜欢喝咖啡”中的“咖啡”与前面的“喜欢喝”密切相关。
- 时间序列预测:在预测股票价格时,前几天的价格变化可以帮助预测未来的价格趋势。
3.2、梯度消失与爆炸
概念:
- 梯度消失和梯度爆炸是反向传播算法中常见的问题,尤其是在深度神经网络和
RNN中。 - 梯度消失:在反向传播过程中,梯度逐渐衰减为接近零的值,导致早期层(或早期时间步)中的权重更新几乎停滞。这会使模型难以学习序列中
较早的依赖关系。 - 梯度爆炸:梯度在反向传播过程中
快速增大,导致权重更新过大,引起数值不稳定和训练失败。
原因:
- 在RNN中,隐藏状态之间的递归计算导致梯度的连乘。对于梯度消失,这种连乘可能导致梯度的
指数衰减;对于梯度爆炸,可能导致梯度的指数增长。 - 激活函数的选择(例如,使用sigmoid或tanh)也可能加剧梯度消失问题,因为这些函数在其饱和区间内的导数很小。
可以看一下sigmoid和tanh的函数、导数关系,直观感受一下:
sigmoid:
tanh:
解决方法:
- 使用LSTM和GRU:
- 长短时记忆网络(LSTM)和门控循环单元(GRU)是RNN的变体,通过引入门控机制有效管理信息流动。
- 这些门控单元(输入门、遗忘门、输出门)允许网络有选择地保留或遗忘信息,从而缓解梯度消失和爆炸问题。
- 梯度裁剪:
- 在反向传播中
限制梯度的最大值,以防止梯度爆炸。 - 梯度裁剪通过将过大的梯度向量
缩放到一个合理的范围来实现。
- 在反向传播中
- 使用合适的激活函数:
- 使用ReLU或其变体(如Leaky ReLU)替代sigmoid或tanh,因为ReLU在正区间的梯度不会消失。
- 正则化技术:
- 采用正则化技术(如Dropout)来减少过拟合和提高模型的泛化能力。
- 初始化技术:
- 使用合适的权重初始化方法(如Xavier初始化或He初始化)来改善训练稳定性。
3.3、总结
- RNN在处理序列依赖性上具有强大的能力,主要挑战是梯度消失和梯度爆炸问题。
- 这些问题在序列很长时尤为明显,因为反向传播通过时间(Backpropagation Through Time, BPTT)过程中,梯度会随着时间步的增加而指数级地缩小或放大。
- 为了解决这些问题,引入了先进的架构 【如LSTM(Long Short-Term Memory)和GRU(Gated Recurrent Unit)等变体】,这些模型通过门控机制有效地管理信息流,缓解了梯度消失和爆炸的问题。
- 还有优化策略(如梯度裁剪)、正则化和适当的初始化等,也能够有效缓解这些问题,从而提升模型的性能和稳定性。、
4、传统的前馈神经网络
传统的前馈神经网络(Feedforward Neural Networks,简称 FNN)是一种最基础的人工神经网络结构,主要用于监督学习任务。
它们由多个神经元(类似于生物神经元的模型)组成,按照层级结构排列,包括输入层、隐藏层和输出层。
4.1、结构
- 输入层:接收外部输入信号,每个节点代表一个特征。
- 隐藏层:介于输入层和输出层之间,可以有一个或多个。隐藏层中的神经元接收前一层的输出,通过激活函数进行处理,再输出到下一层。
- 输出层:产生网络的输出结果,输出层的节点数通常与需要预测的类别数或目标值的维度一致。
4.2、工作原理
- 前向传播:输入信号经过网络的各层,逐层计算并传递,直至输出层。每个神经元对输入的加权求和,再通过激活函数得到输出。
- 激活函数:引入非线性特性,常用的有 Sigmoid、Tanh、ReLU 等,帮助网络学习复杂的非线性关系。
- 损失函数:计算输出预测值与真实值之间的误差,常用的有均方误差(MSE)、交叉熵损失等。
- 反向传播:通过计算损失函数的梯度,将误差从输出层逐层向输入层传播,更新每个连接权重以最小化误差。这是通过梯度下降等优化算法实现的。
4.3、特点
- 单向传播:信号只从输入层向输出层传递,不会有反馈回路。
- 训练过程:基于反向传播算法,通过多次迭代来优化权重,直到损失函数收敛。
- 适用场景:适合解决分类、回归问题,如手写数字识别、图像分类等。
4.4、局限性
- 局部极小值:可能陷入局部极小值,无法找到全局最优解。
- 过拟合:在训练数据上表现良好,但在新数据上可能泛化能力较差。
- 不适合序列数据:由于缺乏记忆能力,无法有效处理时间序列或序列相关的数据(如语音、文本),此类任务通常使用循环神经网络(RNN)或长短期记忆网络(LSTM)来解决。
传统前馈神经网络是深度学习的基础,尽管其功能有限,但在理解和构建更复杂的网络结构(如卷积神经网络CNN和循环神经网络RNN)方面,它们提供了重要的基础知识。
5、CNN与RNN的关系
卷积神经网络(Convolutional Neural Networks,简称 CNN)可以被视为一种特殊类型的前馈神经网络。
它们在设计上继承了前馈神经网络的基本结构,即数据在网络中是单向流动的,从输入层通过隐藏层到输出层。
然而,CNN 在结构上引入了一些独特的层和机制,以更好地处理特定类型的数据,特别是图像数据。
5.1、二者的关系
- 前馈特性:CNN 中的数据流动方向是单向的,类似于传统的前馈神经网络。
- 层次结构:CNN 也由输入层、隐藏层和输出层组成。隐藏层通常包含卷积层、池化层和全连接层。
- 训练过程:与传统的前馈神经网络一样,CNN 也通过反向传播和梯度下降等优化算法进行训练。
5.2、CNN 的独特特性
- 卷积层:通过卷积运算提取数据中的局部特征。卷积层使用多个过滤器(或核)在输入数据上滑动,以识别不同的模式和特征。
- 池化层:进行降维处理,减少数据量和计算量,同时保留重要特征。常用的池化操作有最大池化(Max Pooling)和平均池化(Average Pooling)。
- 权重共享:CNN 的卷积层中的过滤器在整个输入上共享相同的权重,这大大减少了参数数量,提高了模型的训练效率。
- 平移不变性:由于卷积和池化操作,CNN 能够识别输入数据中的特征,即使这些特征在位置上有所变化。
5.3、适用场景
CNN 在图像处理和计算机视觉领域表现出色,如图像分类、目标检测、图像分割等任务。
其设计能够有效捕捉图像中的空间结构和局部依赖性。
5.4、总结
虽然 CNN 是一种前馈神经网络,但其独特的结构使其在处理某些类型的数据时更加高效和准确。
与传统的前馈神经网络相比,CNN 通过引入卷积和池化等操作,实现了对图像数据的更好处理。