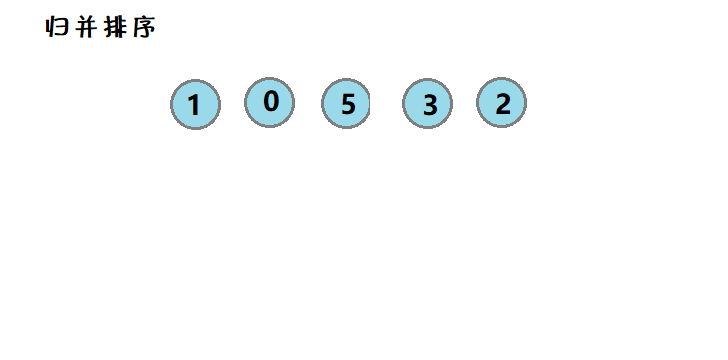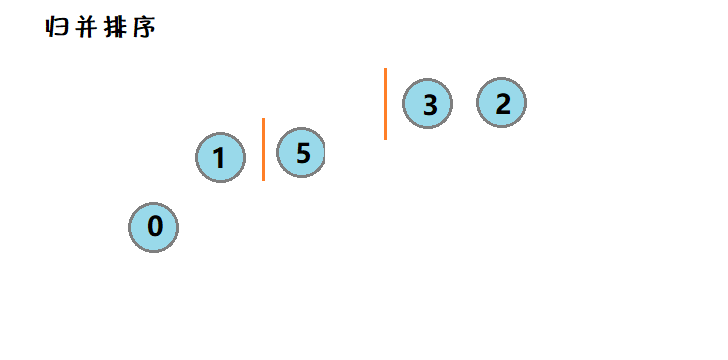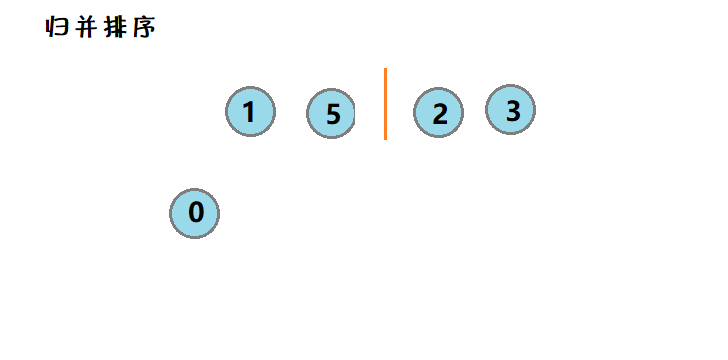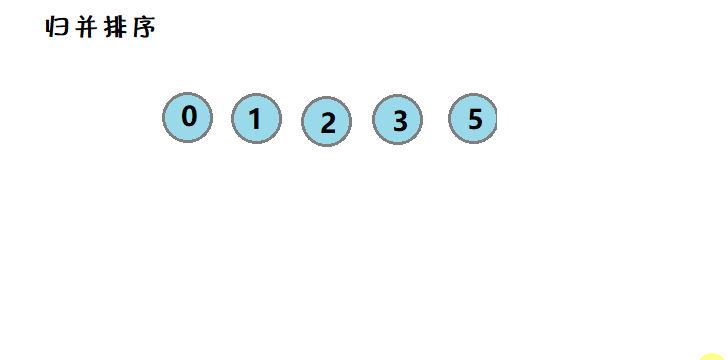目录
排序 (Sorting) 是计算机程序设计中的一种重要操作,它的功能是将一个 数据元素 (或记录)的任意序列,重新排列成一个关键字有序的序列。
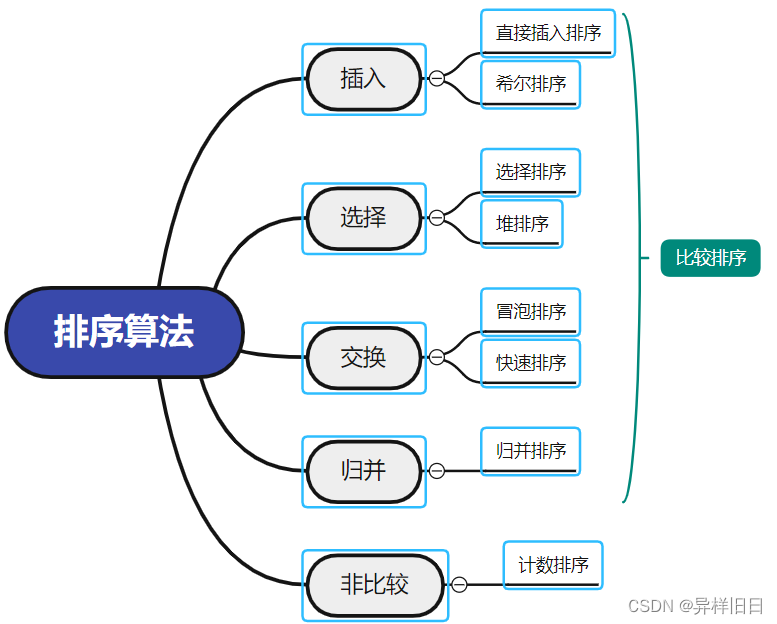
一、常见排序算法
二、实现
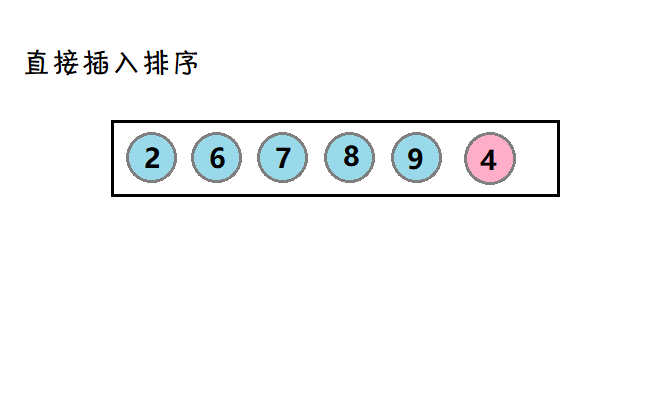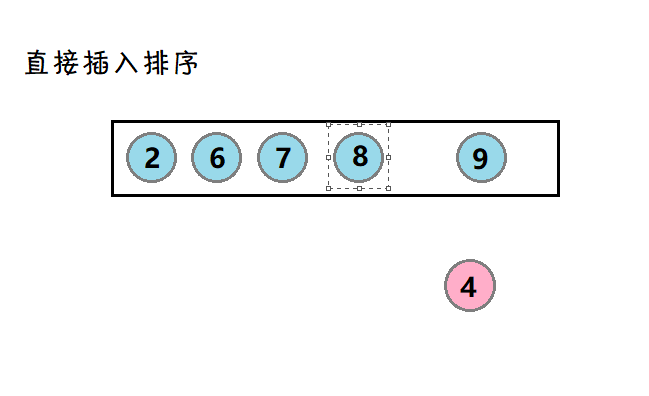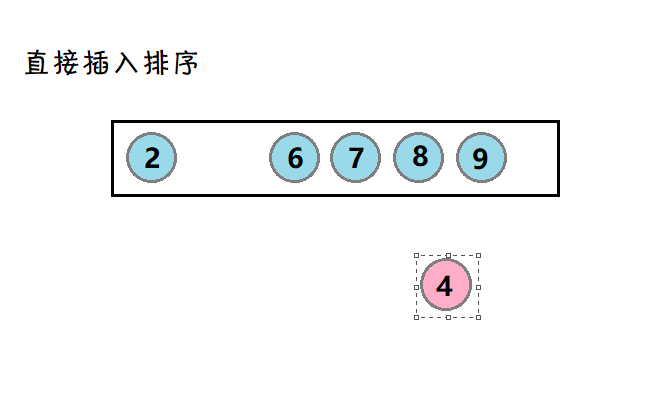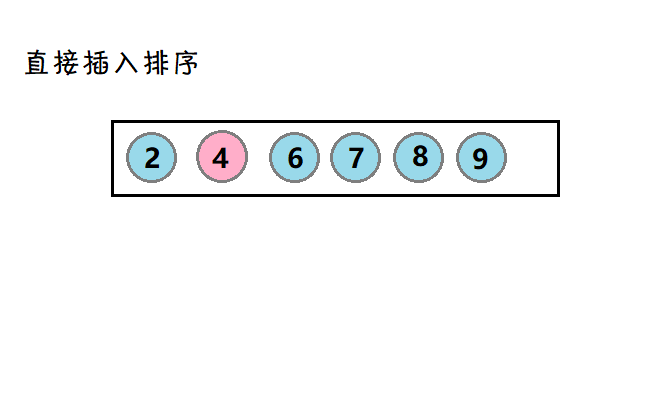
1. 直接插入排序
介绍:将待排的数,和有序的数比较,直到一个合适的位置,然后进行插入。
示图:
将待排数4,与有序数对比,然后插入到(比4小的数)2前面
代码:
// 插入排序(升序)
void InsertSort(int* a, int n)
{
for (int i = 0; i < n-1 ; ++i)
{
int end = i;
//[0,end]为有序数组
//记录下需要插入的数,将end+1的位置空出来
int temp = a[end + 1];
//将需插入的数和有序数组对比
while (end >= 0)
{
//如果大于,则向后移动一位
if (a[end] > temp)
{
a[end + 1] = a[end];
end--;
}
else//否则,退出
{
break;
}
}
//下标(end+1)就是合适的插入位置
a[end + 1] = temp;
}
}
效率:时间复杂度为 O ( N 2 ) O(N^2) O(N2)
如果原始数组为升序有序,则直接会break,时间复杂度为 O ( N ) O(N) O(N)。
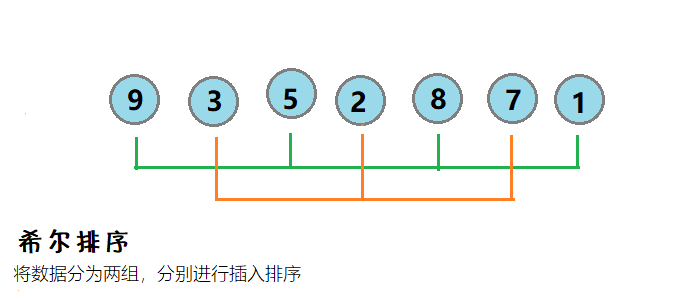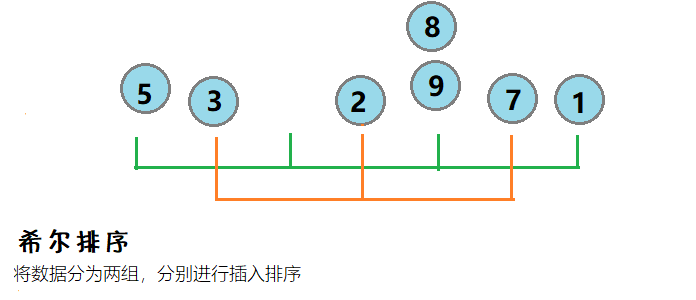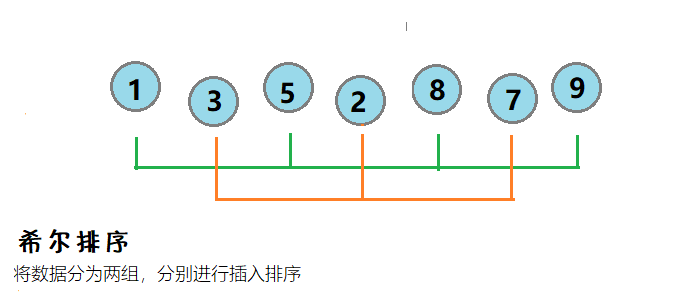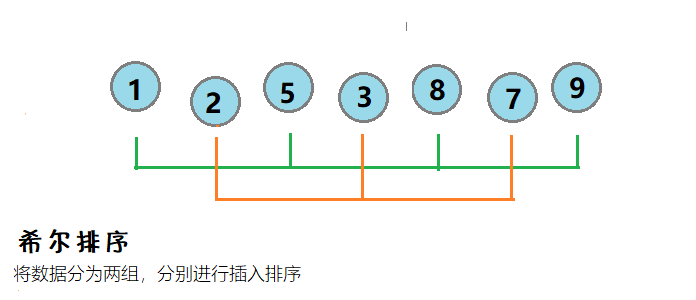
2.🌟希尔排序
介绍:利于直接插入排序的思想,如果所排的数据接近有序,则排序效率非常高。希尔排序,是将数据非为若干组,然后对每组的数据进行插入排序,使之逐渐有序。
其中如果分组为1,则等于直接插入排序
图示:
将数据分为9 5 8 1和3 2 7两组,分别进行插入排序,得到1 2 5 3 8 7 9,逐渐接近有序
代码:
void Swap(int* p1, int* p2)
{
int temp = *p1;
*p1 = *p2;
*p2 = temp;
}
// 希尔排序(升序)
void ShellSort(int* a, int n)
{
int group = n;
//逐渐将分组缩小,直至分组为1
while (group > 1)
{
//一般分组每次缩小1/3
//+1:为确保最后分组为1
group = group / 3 + 1;
//每个数依次在它所在组中插入排序
for (int i = 0; i < n - group; i++)
{
int end = i;//每组排序好的最后一个元素
int temp = a[end + group];//对应组下一个要插入的元素
//思路同插入排序,只不过操作的是对应组中的元素
while (end >= 0)
{
if (a[end] > temp)
{
a[end + group] = a[end];
end -= group;
}
else
{
break;
}
}
a[end + group] = temp;
}
}
}
效率:时间复杂度大约为 O ( N 1.3 ) O(N^{1.3}) O(N1.3)
因为希尔排序的时间复杂度非常难算,感兴趣的可以去百度。
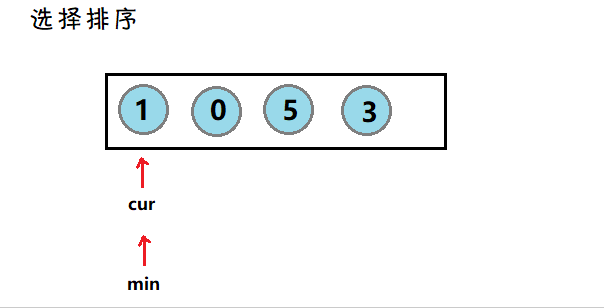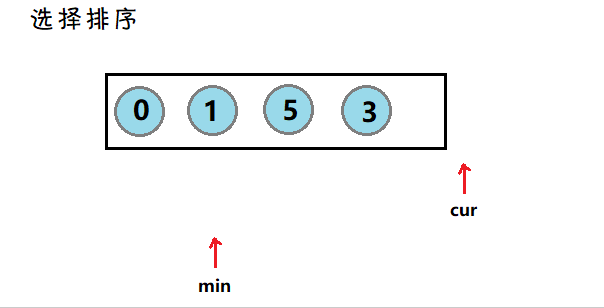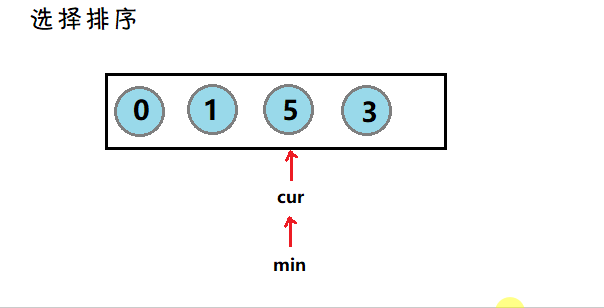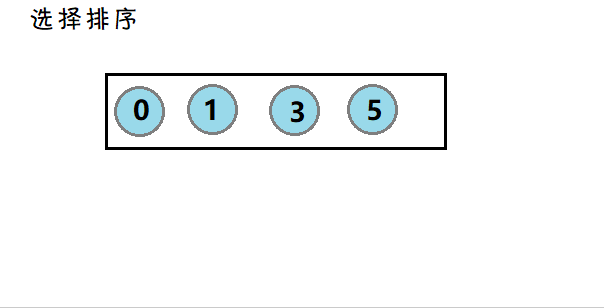
3. 选择排序
介绍:每一次都遍历一遍数据,选出最小(大)的元素,放在起始点。
图示:
代码:
// 选择排序(升序)
void SelectSort(int* a, int n)
{
int begin = 0;
int end = n - 1;
//每遍历一遍,选出最大和最小
while (begin < end)
{
int maxi = end;
int mini = begin;
for (int i = begin; i <= end; i++)
{
if (a[maxi] < a[i])
{
maxi = i;
}
if (a[mini] > a[i])
{
mini = i;
}
}
Swap(&a[begin], &a[mini]);
//如果最大的数下标为begin,被上一步改变
if (maxi == begin)
{
maxi = mini;
}
Swap(&a[end], &a[maxi]);
begin++;
end--;
}
}
效率:时间复杂度为 O ( N 2 ) O(N^2) O(N2)
虽然一次遍历找一个,优化为每趟找两个,只是每趟比较次数的等差数列的公差由1变为2,但是大 O O O的渐进表示法都为 O ( N 2 ) O(N^2) O(N2)
4.🌟堆排序
简介:该部分涉及堆的相关知识,
详情请见另一篇:堆
效率:时间复杂度为 O ( N l o g 2 N ) O(Nlog_2N) O(Nlog2N)
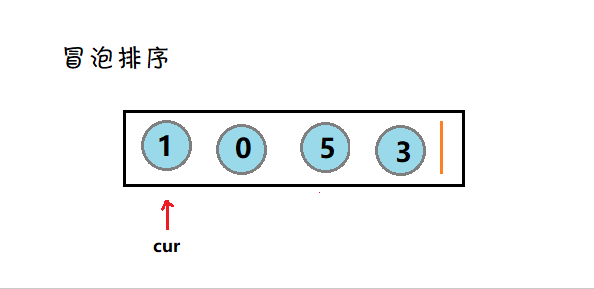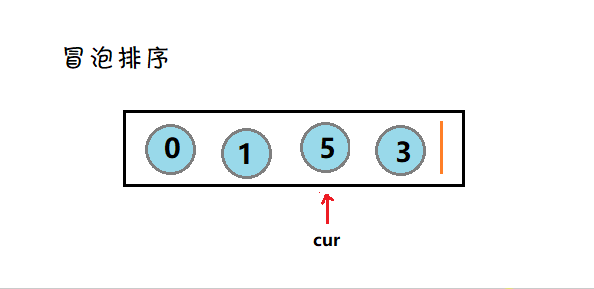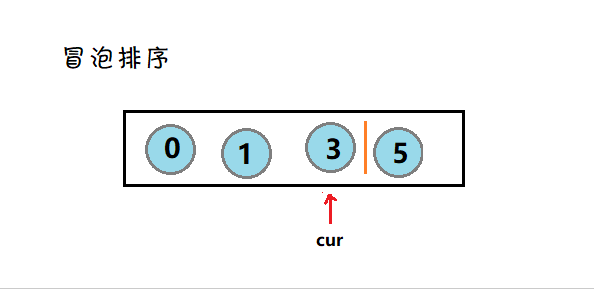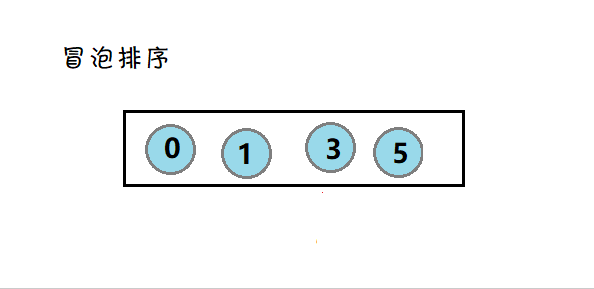
5. 冒泡排序
简介:冒泡的思想就是遍历数据进行比较,然后把最大(小)的数交换到最后位置。
图示:
代码:
// 冒泡排序(升序)
void BubbleSort(int* a, int n)
{
//最多要遍历n-1次
for (int i = 0; i < n - 1; ++i)
{
int flag = 0;
for (int j = 0; j < n - i - 1; ++j)
{
//当前的数与下一个数进行比较
if (a[j] > a[j + 1])
{
Swap(&a[j], &a[j + 1]);
flag = 1;
}
}
//如果没有进行交互,则已经排序完成了
if (flag == 0)
{
break;
}
}
}
效率:时间复杂度 O ( N 2 ) O(N^2) O(N2)
因为优化了退出条件,因此对于已排序的原始数据,时间复杂度为 O ( N ) O(N) O(N)
7. 🌟快速排序
简介:开始时,任取数据中的某一元素为基准,然后将小于该元素的放在左边,大于该元素的放在右边,把剩余数据分为两个序列。然后再对左右序列重复该过程,直到每个元素都在对应位置
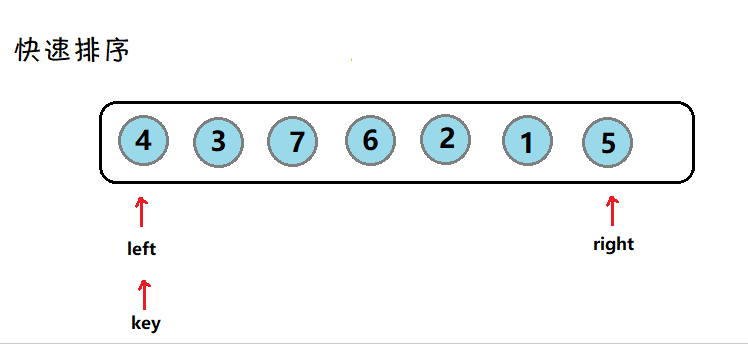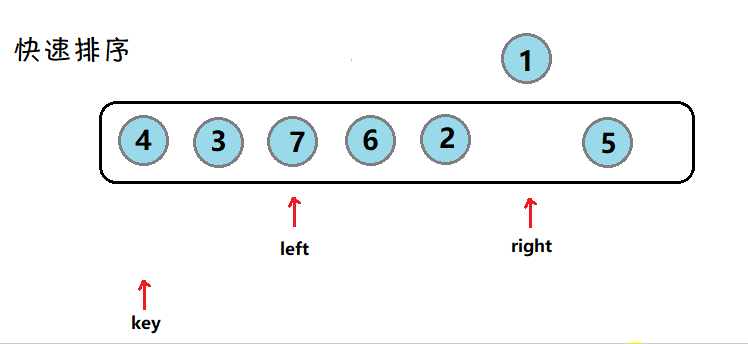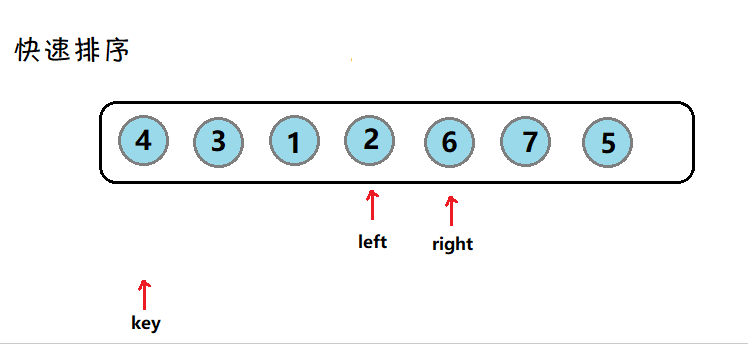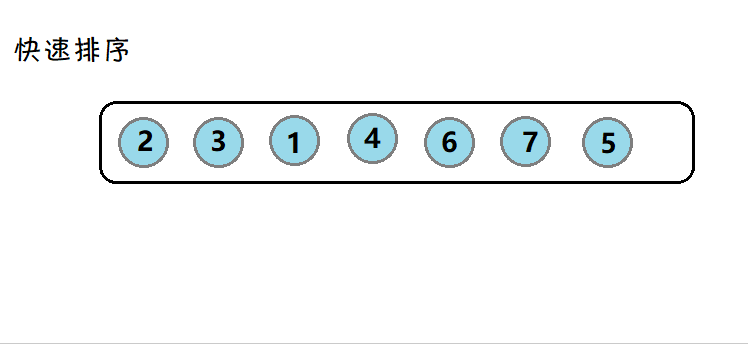
(hoare版本)图示:
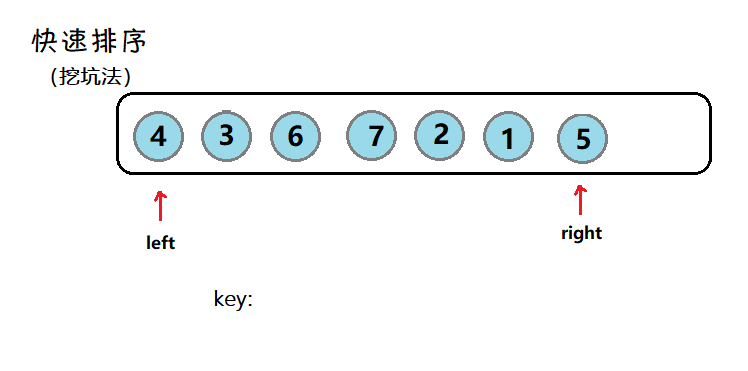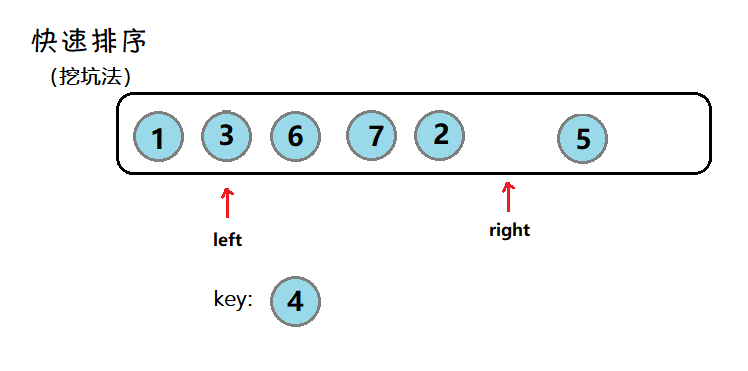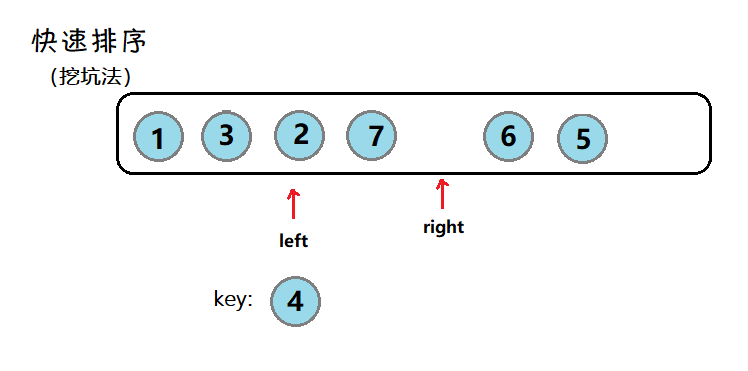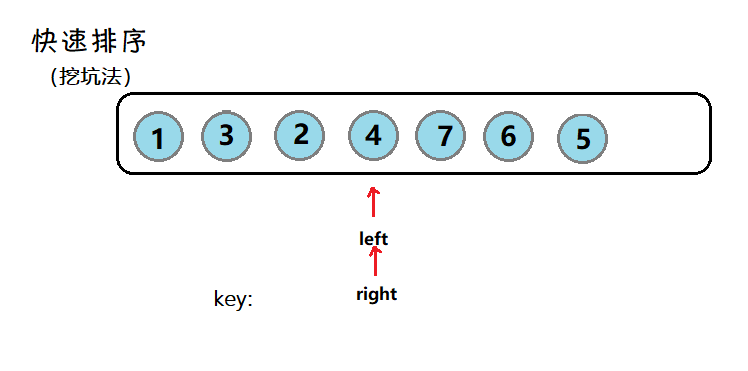
对数组4 3 6 7 2 1 5,以第一个4为关键数,升序排列,大于4的都放在右边,小于4的放在左边。得到结果2 3 1 4 6 7 5
先移动右指针,走到小于4的数停下,再移动左指针,找到大于4的数停下,交换两数,然后继续,直到左右指针相遇,因为左指针后走,因此停下的位置一定是小于等于4的,再和4交换。
代码:
void QuickSort(int* a, int left, int right)
{
//如果只有一个数,直接返回
if (left >= right)
{
return;
}
//记录起始和结束
int begin = left;
int end = right;
//默认key为第一个数
int keyi = left;
while (left < right)
{
//先移动右指针,找到比key小的数
while (left < right && a[right] >= a[keyi])
{
right--;
}
//再移动左指针,找到比key大的数
while (left < right && a[left] <= a[keyi])
{
left++;
}
Swap(&a[left], &a[right]);
}
//right位置一定小于等于keyi位置数据
Swap(&a[right], &a[keyi]);
keyi = right;
//分别排左右序列
//[left,keyi-1], keyi, [keyi-1,right]
QuickSort(a, begin, keyi - 1);
QuickSort(a, keyi + 1, end);
}
效率:时间复杂度 O ( N l o g 2 N ) O(Nlog_2N) O(Nlog2N)。每次走一趟,一共走 l o g 2 N log_2N log2N次
7.1 其他版本的快排
挖坑法:
void QuickSort(int* a, int left, int right)
{
if (left >= right) return;
int begin = left, end = right;
//默认key为第一个数
int key = a[left];
int piti = left;//坑的位置
while (left < right)
{
//右指针先走
while (left < right && a[right] >= key)
{
--right;
}
a[piti] = a[right];
piti = right;
//左指针走
while (left < right && a[left] <= key)
{
++left;
}
a[piti] = a[left];
piti = left;
}
//最后留下的坑位来存放key
a[piti] = key;
QuickSort(a, begin, keyi - 1);
QuickSort(a, keyi + 1, end);
}
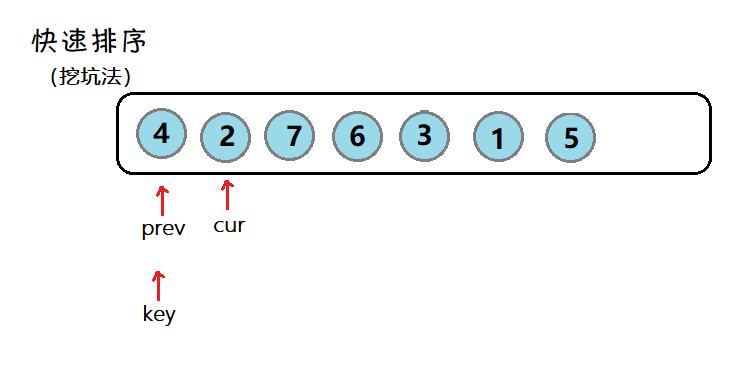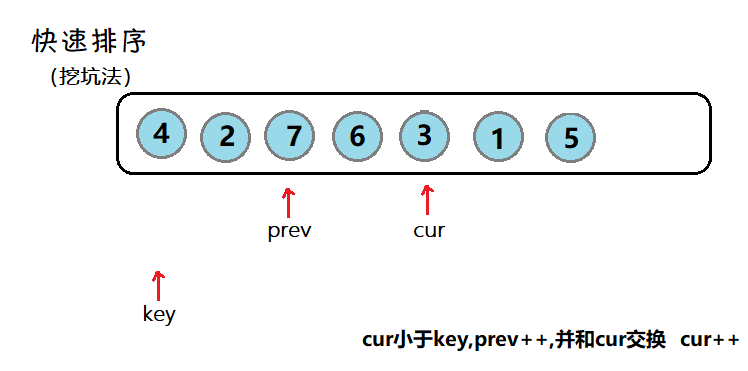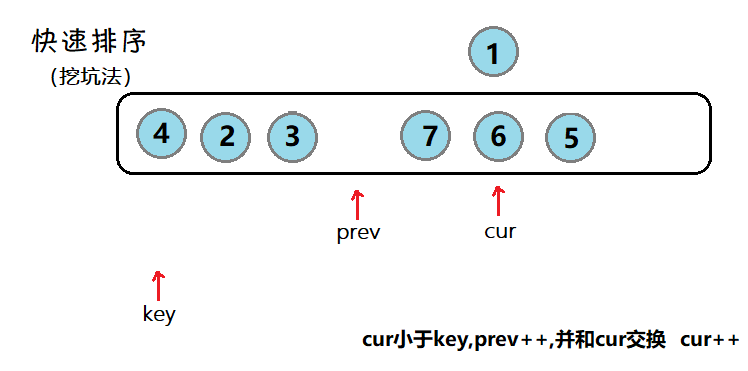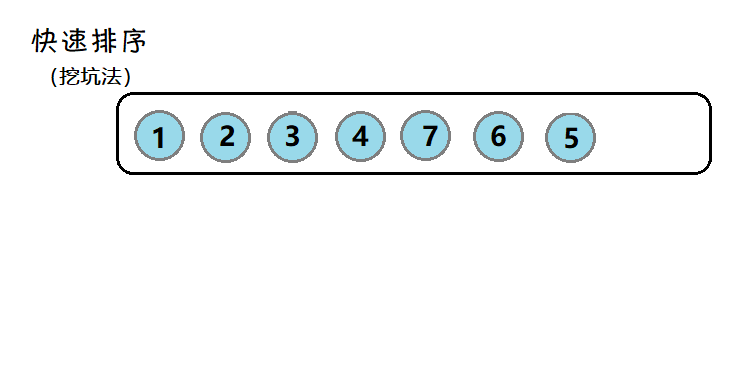
前后指针:
用cur来找到小于key的元素,prev找到大于key的元素。刚开始时,cur还未遇见大于等于key的元素时,cur和prev一起向右。(如果此步,不好理解的话,可以自己动手画画)
void QuickSort(int* a, int left, int right)
{
if (left >= right) return;
int begin = left, end = right;
int keyi = left; //默认key为第一个数
int prev = left;
int cur = left + 1;
while (cur <= right)
{
//当cur小于key,且prev++后不等于cur,才会交换
if (a[cur] < a[keyi] && ++prev!=cur)
{
Swap(&a[cur], &a[prev]);
}
++cur;//cur一直向后走
}
Swap(&a[keyi], &a[prev]);
keyi = prev;
QuickSort(a, begin, keyi - 1);
QuickSort(a, keyi + 1, end);
}
7.2 优化
三数取中:
因为key的选取会影响快速排序的效率,其中,如果key每次都是是中间的数,接近二分,效率最高 O ( N l o g 2 N ) O(Nlog_2N) O(Nlog2N);如果每次都是最小(大)的数,则效率最低 O ( N 2 ) O(N^2) O(N2),因为总会出现[key]+[未排序数据]
//找到前中后三个数中,中间的那个
int GetMid(int* a, int left, int right)
{
int mid = (left + right) / 2;
if (a[mid] < a[left])
{
if (a[right] > a[left])
{
return left;
}
else if (a[right] < a[mid])
{
return mid;
}
else
{
return right;
}
}
else
{
if (a[right] < a[left])
{
return left;
}
else if (a[right] > a[mid])
{
return mid;
}
else
{
return right;
}
}
}
结合插入排序:
对于一组比较大的数据,在递归后期,小范围的序列会有很多。因此可以在划分的范围足够小后,直接使用插入排序,避免继续向下递归。(tips:最后一次的递归次数占总递归次数的一半左右)
void QuickSort(int* a, int left, int right)
{
if (left >= right)
{
return;
}
int keyi = left;
int end = right;
//三数取中
int midi = GetMid(a, left, right);
Swap(&a[midi], &a[keyi]);
//使用插入排序
if (right - left < 13)
{
InsertSort(a + left, right - left + 1);
}
else
{
int begin = left, end = right;
while (left < right)
{
//先移动右指针,找到比key小的数
while (left < right && a[right] >= a[keyi])
{
right--;
}
//再移动左指针,找到比key大的数
while (left < right && a[left] <= a[keyi])
{
left++;
}
Swap(&a[left], &a[right]);
}
Swap(&a[right], &a[keyi]);
keyi = right;
QuickSort(a, begin, keyi - 1);
QuickSort(a, keyi + 1, end);
}
}
7.3 ⭐非递归
递归的思想,比较容易写,但是它占用栈区空间,如果数据足够大,是可能发生栈溢出错误的。
保持快速排序的思路不变,显然循环无法实现,但是我们可以用栈来模拟递归。
每次将要比较的序列的范围[bigin,end],记录到栈中,每次循环开始,出栈,结束后又将新划分的左右序列入栈。
快速排序 非递归实现
void QuickSortNonR(int* a, int left, int right)
{
Stack st;
StackInit(&st);
StackPush(&st, left);
StackPush(&st, right);
while (!StackEmpty(&st))
{
//出栈,得到要排序的范围[bigin,end]
int end = StackTop(&st);
StackPop(&st);
int begin = StackTop(&st);
StackPop(&st);
//排序,使key放到正确位置
int keyi = begin;
int prev = begin;
int cur = begin + 1;
while (cur <= end)
{
//当cur小于key,且prev++后不等于cur,才会交换
if (a[cur] < a[keyi] && ++prev!=cur)
{
Swap(&a[cur], &a[prev]);
}
++cur;//cur一直向后走
}
Swap(&a[keyi], &a[prev]);
keyi = prev;
//将新的左右序列[bigin,keyi-1],[keyi+1,end]入栈
if (begin < keyi - 1)
{
StackPush(&st, begin);
StackPush(&st, keyi - 1);
}
if (keyi + 1 < end)
{
StackPush(&st, keyi + 1);
StackPush(&st, end);
}
}
StackDestroy(&st);
}
同样的,其实可以用队列来实现快速排序的非递归。
思路:将bigen end入队列,循环开始时,出队列找到要排序的范围[begin,end],排序完成后将左右序列[bigin,keyi-1],[keyi+1,end]入队列
和栈实现不同的是:栈是以递归的方式,排完左序列后才会开始排右,而队列则是排左,排右交替进行。
7. 🌟归并排序
简介:采用分治实现,将数据划分为两等份分别有序的序列,然后合并。
图示:
对数据1 0 5 3 2,进行归并排序,首先将数据分为两份1 0 5和3 2,在向下划分,直至最小的,然后在将两两归并,逐渐形成有序序列。
代码:
void _MergeSort(int* a, int n, int begin, int end, int* temp)
{
if (begin >= end)
{
return;
}
int mid = (begin + end) / 2;
//由图示,可见,后序,深度优先
//[begin,mid] [mid+1,end]
_MergeSort(a, n, begin, mid, temp);
_MergeSort(a, n, mid+1, end, temp);
//将[begin,mid] [mid+1,end]两个序列按顺序合并
int begin1 = begin, end1 = mid;
int begin2 = mid + 1, end2 = end;
int i = begin;
while (begin1 <= end1 && begin2 <= end2)
{
// "<"升序
if (a[begin1] < a[begin2])
{
temp[i++] = a[begin1++];
}
else
{
temp[i++] = a[begin2++];
}
}
//处理某个序列的剩余数据
while (begin1 <= end1)
{
temp[i++] = a[begin1++];
}
while (begin2 <= end2)
{
temp[i++] = a[begin2++];
}
//拷贝到原数组中,也可以使用库函数
//memcpy(a + begin, tmp + begin, (end - begin + 1)*sizeof(int));
for (int j = begin; j <= end; ++j)
{
a[j] = temp[j];
}
}
// 归并排序递归实现
void MergeSort(int* a, int n)
{
//因为有两个序列归并一起,因此需要额外的空间存放,temp为额外空间
int* temp = (int*)malloc(sizeof(int) * n);
if (temp == NULL)
{
perror("malloc failed\n");
exit(-1);
}
_MergeSort(a, n, 0, n - 1, temp);
free(temp);
}
效率:时间复杂度 O ( N l o g 2 N ) O(Nlog_2N) O(Nlog2N)
严格的二分,会比快速排序更优,但是需要额外的空间 O ( N ) O(N) O(N)
7.1 ⭐非递归
递归,同样面临栈溢出的风险。
由归并排序的思想,先将数据划分为1个数一组的序列,然后将相邻的两个组合并,然后再分为2个数一组的序列,再进行合并,直到最后划分整个序列为一组。
tips:由于是按照1,2,4,8…逐渐划分的,但是原始数据的长度可能并不是严格的 2 n 2^n 2n个,所有划分出的组可能会出现越界问题,需要处理。
代码:
// 归并排序非递归实现
void MergeSortNonR(int* a, int n)
{
//需要的额外空间
int* temp = (int*)malloc(sizeof(int) * n);
int grap = 1;//开始时一组有1个数
while (grap < n)
{
//[j,j+grap-1] 与 [j+grap,j+2*grap-1] 按序合并
for (int j = 0; j < n; j += grap*2)
{
int begin1 = j, end1 = j+grap-1;
int begin2 = j + grap, end2 = j + 2 * gap - 1;
//修正
//end1数组越界
if (end1 >= n)
{
end1 = n - 1;
begin2 = n;
end2 = n - 1;
}
//begin2数组越界
else if (begin2 >= n)
{
begin2 = n;
end2 = n - 1;
}
//end2数组越界
else if (end2 >= n)
{
end2 = n - 1;
}
int i = begin1;
while (begin1 <= end1 && begin2 <= end2)
{
// "<"升序
if (a[begin1] < a[begin2])
{
temp[i++] = a[begin1++];
}
else
{
temp[i++] = a[begin2++];
}
}
while (begin1 <= end1)
{
temp[i++] = a[begin1++];
}
while (begin2 <= end2)
{
temp[i++] = a[begin2++];
}
}
//拷贝到原数组中
memcpy(a, temp, sizeof(int)*n);
//每次每组扩大2倍
grap *= 2;
}
free(temp);
}
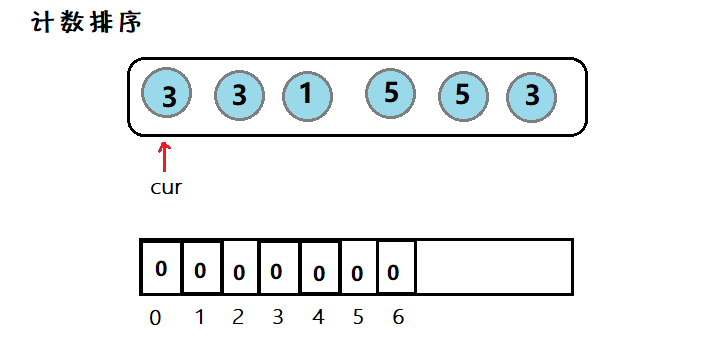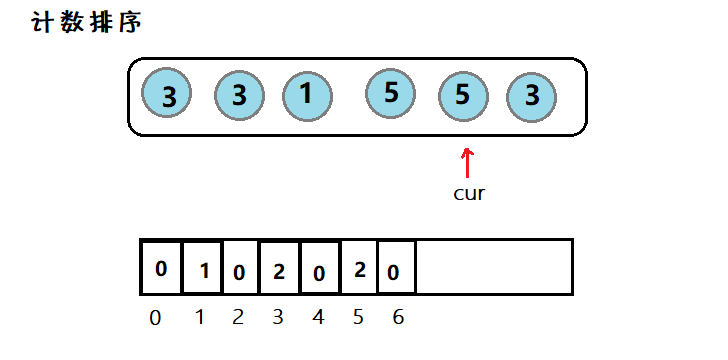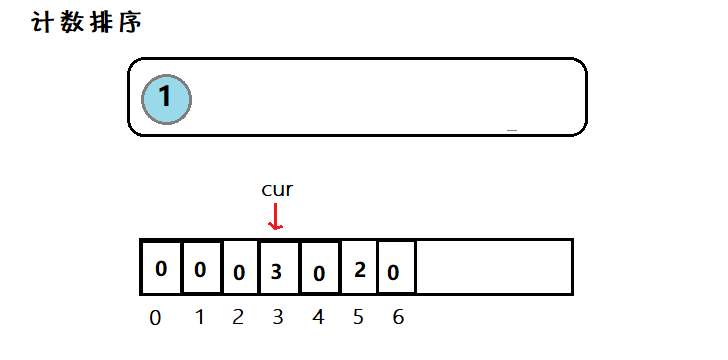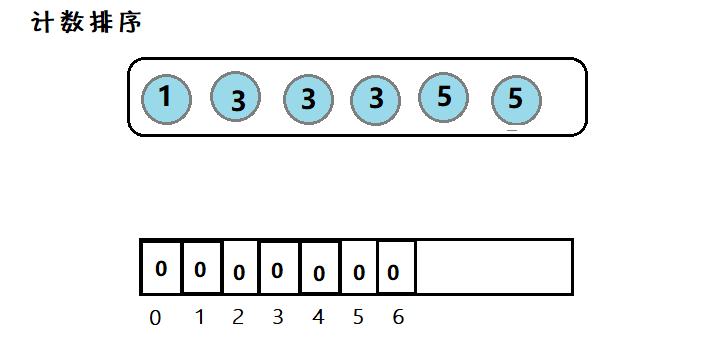
8. 计数排序
简介:因为数组下标为整数,因此对于整型数据,我们可以遍历一般然后计数,最后再遍历一般写入。
图示:
利用数组下标,来在该空间位置存放个数,然后在遍历数组,使之有序。但是适用范围有限。
代码:
// 计数排序
void CountSort(int* a, int n)
{
//找到数据中的max与min的数
int max = a[0], min = a[0];
for (int i = 1; i < n; ++i)
{
if (a[i] > max)
max = a[i];
if (a[i] < min)
min = a[i];
}
//这所需开辟数组大小为
//所开辟数组[0,range-1]
//与原数据中[mini,maxi],构成映射
int range = max - min + 1;
int* count = (int*)calloc(range, sizeof(int));
//计数
for (int i = 0; i < n; ++i)
{
count[a[i]-min]++;
}
//进行排序
int j = 0;
for (int i = 0; i < range; ++i)
{
while (count[i]--)
{
//从映射中还原
a[j++] = i + min;
}
}
free(count);
}
效率:时间复杂度为 O ( N ) O(N) O(N)
三、总结
稳定性:对于原数据中,相同值、不同先后顺序的元素,进行排序后,如果其先后顺序任未改变,则称该排序算法是稳定的。
通常稳定主要用于对一组原始数据(每个元素有多个属性值),按照不同规律进行排序时才非常重要。
1. 分析
下面👇同种算法,时间复杂度最好或最坏的情况,其代码可能不同(有无优化)
| 排序算法 | 平均时间复杂度 | 最好 | 最坏 | 空间复杂度 | 稳定性 |
|---|---|---|---|---|---|
| 直接插入排序 | O ( n 2 ) O(n^2) O(n2) | O ( n ) O(n) O(n) | O ( n 2 ) O(n^2) O(n2) | O ( 1 ) O(1) O(1) | 稳定 |
| 希尔排序 | O ( n 1.3 ) O(n^{1.3}) O(n1.3) | O ( n 1.3 ) O(n^{1.3}) O(n1.3) | O ( n 2 ) O(n^2) O(n2) | O ( 1 ) O(1) O(1) | 不稳定 |
| 选择排序 | O ( n 2 ) O(n^2) O(n2) | O ( n 2 ) O(n^2) O(n2) | O ( n 2 ) O(n^2) O(n2) | O ( 1 ) O(1) O(1) | 不稳定 |
| 堆排序 | O ( n l o g 2 n ) O(nlog_2n) O(nlog2n) | O ( n l o g 2 n ) O(nlog_2n) O(nlog2n) | O ( n l o g 2 n ) O(nlog_2n) O(nlog2n) | O ( 1 ) O(1) O(1) | 不稳定 |
| 冒泡排序 | O ( n 2 ) O(n^2) O(n2) | O ( n ) O(n) O(n) | O ( n 2 ) O(n^2) O(n2) | O ( 1 ) O(1) O(1) | 稳定 |
| 快速排序 | O ( n l o g 2 n ) O(nlog_2n) O(nlog2n) | O ( n l o g 2 n ) O(nlog_2n) O(nlog2n) | O ( n 2 ) O(n^2) O(n2) | O ( l o g 2 n ) O(log_2n) O(log2n)~ O ( n ) O(n) O(n) | 不稳定 |
| 归并排序 | O ( n l o g 2 n ) O(nlog_2n) O(nlog2n) | O ( n l o g 2 n ) O(nlog_2n) O(nlog2n) | O ( n l o g n ) O(nlog_n) O(nlogn) | O ( n ) O(n) O(n) | 稳定 |
| 计数排序 | O ( n ) O(n) O(n) | O ( n ) O(n) O(n) | O ( n ) O(n) O(n) | O ( m a x ( n , r a n g e ) ) O(max(n,range)) O(max(n,range)) | 无 |
该总结,还是要结合前面详细的讲解,自己要能够分析出来。
🦀🦀观看~~