263.丑数

如果因数包含指定质因数，就说明能被该质因数整除。

那我们就不断去除它的这几个质因数，如果已经不含它指定的质因数了且当前数值不为一，那么就不是丑数。否则为丑数

class Solution {
    public boolean isUgly(int n) {
        //非正数
        if(n <= 0){
            return false;
        }
        //一直除指定的质因数
        while(n != 1){
            //用来检测是否还能继续除指定质因数了
            int temp = n;
            //当前包含因数2
            while(n % 2 == 0){
                n >>= 1;
            }
            //当前包含因数3
            while(n % 3 == 0){
                n /= 3;
            }
            //当前包含因数5
            while(n % 5 == 0){
                n /= 5;
            }
            //已经不能被2或3或5整除了
            if(n == temp){
                return false;
            }
        }

        return true;
    }
}

264.丑数 ||

采用了哈希表去重，优先队列（小根堆）去不断存储并更新最小的丑数

class Solution {
    public int nthUglyNumber(int n) {
        //记录丑数
        int urgy = 0;
        //记录质因子
        int [] arr = {2, 3, 5};
        //优先队列存储所有丑数并自动排序
        Queue<Long> queue = new PriorityQueue<Long>();
        //用哈希表去重
        Set set = new HashSet();
        //初始化
        queue.add(1L);
        set.add(1L);
        //循环寻找第N个丑数
        for(int i = 0; i < n; i++){
            //获取当前丑数
            long curr = queue.poll();
            urgy = (int)curr;            
            //基于当前丑数产生新丑数
            for(int num : arr){
                if(set.add(curr * num)){
                    queue.add(curr * num);
                }                
            }
        }
        //返回结果
        return urgy;
    }
}

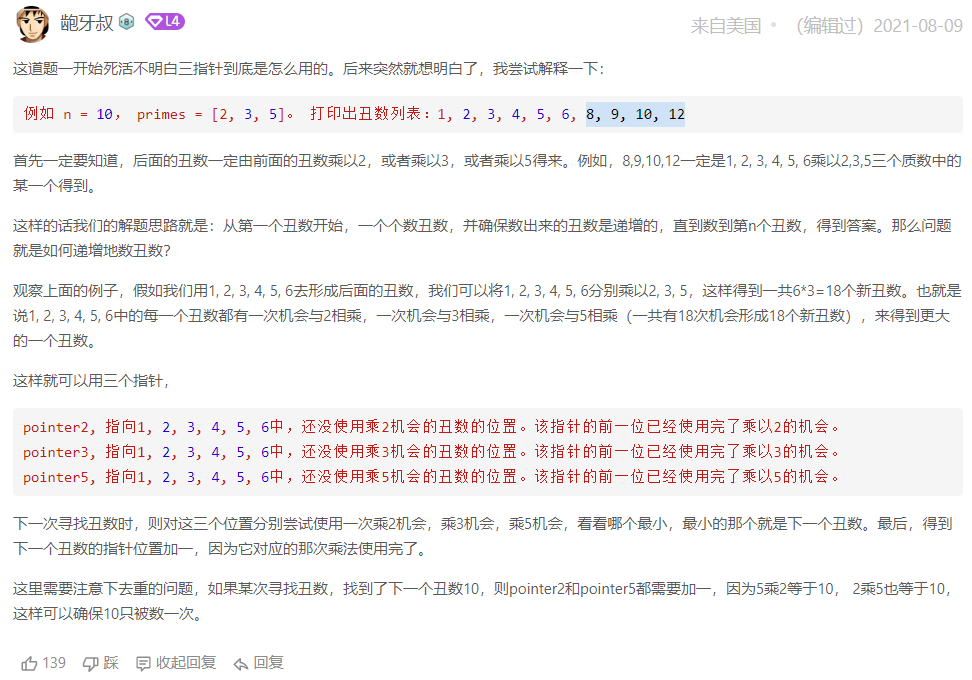
这种方法比较耗时，新方法采用了动态规划三指针法，因为新丑数都是基于已经确定的原丑数得出来的，所以我们把原丑数想象为三组，分别与指定的质因数相乘，谁最小就将当前丑数定为谁，再将对应指针移动到下一位。【此处引用一个大佬的思路帮助理解，因为是评论就没给出原文链接】

class Solution {
    public int nthUglyNumber(int n) {
        //三指针法
        int [] idx = {0, 0, 0};
        //保存丑数
        int [] urgy = new int[n];
        //初始化
        urgy[0] = 1;
        //循环构造最小丑数
        for(int i = 1; i < n; i++){
            //原来的丑数分别与2、3、5相乘
            int num1 = urgy[idx[0]] * 2;
            int num2 = urgy[idx[1]] * 3;
            int num3 = urgy[idx[2]] * 5;
            //取最小值
            int min_num = Math.min(num1, Math.min(num2, num3));
            urgy[i] = min_num;
            //将对应idx移动到下一位
            if(min_num == num1){
                idx[0]++;
            }
            if(min_num == num2){
                idx[1]++;
            }
            if(min_num == num3){
                idx[2]++;
            }
        }
        //返回结果
        return urgy[n - 1];
    }
}