637. 二叉树的层平均值

题目链接

637. 二叉树的层平均值

标签

树 深度优先搜索 广度优先搜索 二叉树

思路

本题考查了二叉树的 层序遍历，层序遍历的思想是 广度优先搜索，广度优先搜索需要使用 队列，操作如下：

1. 创建一个队列，用于保存每层节点。
2. 先将根节点放入队列，代表遍历第一层。
3. 只要队列不为空，就进行如下操作：
   1. 获取本层节点的个数。
   2. 遍历本层的所有节点，遍历操作如下：
      1. 取出当前节点。
      2. 如果当前节点的左子节点不为 null，则将其放到队列中，等待下一层节点的遍历。
      3. 如果当前节点的右子节点不为 null，则将其放到队列中，等待下一层节点的遍历。
      4. 针对当前节点进行某种操作：使用一个变量统计本层节点之和。
   3. 针对本层节点进行某种 统计 操作：计算本层节点的平均值，并将其放到结果链表中。
4. 遍历完整个二叉树，返回结果。

代码

class Solution {
    public List<Double> averageOfLevels(TreeNode root) {
        List<Double> res = new ArrayList<>(); // 存储结果(每层节点的平均值)的链表

        LinkedList<TreeNode> queue = new LinkedList<>(); // 保存每层节点的队列
        queue.offer(root); // 先将根节点放入队列，即遍历第一层
        while (!queue.isEmpty()) { // 直到队列为空，才退出循环
            double sum = 0; // 计算本层节点的和

            int size = queue.size(); // 获取本层节点的数量
            for (int i = 0; i < size; i++) { // 遍历本层所有节点
                TreeNode curr = queue.poll(); // 取出 当前节点
                
                TreeNode left = curr.left; // 获取当前节点的 左子节点
                if (left != null) { // 如果 左子节点 不为 null
                    queue.offer(left); // 则将其放到队列中，等待下一层遍历
                }
                
                TreeNode right = curr.right; // 获取当前节点的 右子节点
                if (right != null) { // 如果 右子节点 不为 null
                    queue.offer(right); // 则将其放到队列中，等待下一层遍历
                }

                sum += curr.val; // 求和
            }

            res.add(sum / size); // 计算平均值
        }
        return res;
    }
}

67. 二进制求和

题目链接

67. 二进制求和

标签

位运算 数学 字符串 模拟

思路

本题是一道 模拟题，如果是十进制，则本题就是 高精度 问题，以下写出一种模版，只需要改变 base 进制，就可以使用不同的进制进行计算。

可以想一想小学一年级学的 列竖式计算两数之和，高精度的解决方案就是它：

1. 将两个数的个位对齐，写出来。
2. 对每一位，有如下操作：
   1. 将两个数的相同位加在一起。此外，还要加上 进位 carry，进位是通过 满 n 进一 得到的，这里的 n 就是进制。如果有一个数的位数不够，则认为这个数的这一位为 0。
   2. 对于加起来的和，如果它大于进制，则进一，并将剩余的数（和 对 进制 取余）写在结果的这一位上；否则直接将和写在结果的这一位上。
3. 最后，看是否还应该进位，如果需要，则再添加一位 1。

由于 题目传入的字符串和要求返回的字符串都是从高位到低位的，而 在计算时是从低位到高位的，所以要注意在计算时颠倒字符串，并将计算结果反转之后再返回。

代码

class Solution {
    public String addBinary(String a, String b) {
        final int base = 2; // 进制，本题为 二进制

        StringBuilder builder = new StringBuilder(); // 拼接数字的拼接器
        char[] aC = a.toCharArray(), bC = b.toCharArray();
        int aLen = aC.length, bLen = bC.length;
        int len = Math.max(aLen, bLen); // 获取较长字符串的长度

        int carry = 0; // 是否要进一，如果要进一，则为 1；否则为 0
        for (int i = 0; i < len; i++) {
        	// 注意 aC/bC[i] 是字符，需要通过 减去 '0' 来将其转化为 数字
            int operand1 = i < aLen ? (aC[aLen - i - 1] - '0') : 0;
            int operand2 = i < bLen ? (bC[bLen - i - 1] - '0') : 0;
            int sum = operand1 + operand2 + carry;
            carry = sum / base; // 查看是否需要进一
            sum %= base; // 获取剩余的数
            builder.append(sum);
        }
        
        if (carry > 0) { // 如果还需要进位
            builder.append(1); // 则再添加一位 1
        }
        
        builder.reverse(); // 先将结果反转
        return builder.toString(); // 再返回
    }
}

399. 除法求值

题目链接

399. 除法求值

标签

深度优先搜索 广度优先搜索 并查集 图 数组 字符串 最短路

思路

导入

本题不算中等题，理应为困难题，主要与 并查集、数学 有关，操作十分复杂。可以先看看 990. 等式方程的可满足性，990 题是本题的简单版本，尽量理解 990 题中的并查集的使用。此外，希望大家看一看并查集的 路径压缩，这在本题中很重要。

value 属性

如果能够理解 990 题，那么离解决本题就不远了。本题的并查集中每个节点都比 990 题多了一个值 value，其保存了 本节点 与 其父节点 的比值，即有 $$value[i]=\frac{i}{parent[i]}$$ 请记住这点，在 find() 和 union() 中很重要。注意：其中的 i, parent[i] 不是索引，没有实际意义，只是充当有逻辑意义的占位符，这个比值是从 values 数组中获得的。

find() 方法

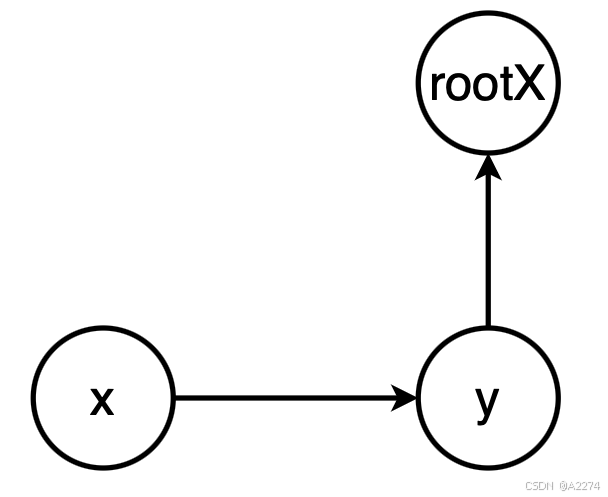
在 find() 时需要 压缩路径，因为这样可以避免一些计算。例如下面的并查集，如果想要查询 x 与 rootX 的比值，就必须计算两次；但如果直接让 x 指向 rootX，这时只需要获取 value[x] 即可。具体的操作为先保存父节点，再递归获取根节点，最后更新本节点的 value，从 本节点与父节点的比值 变为 本节点与根节点的比值。等式如下：$$\frac{x}{rootX}=\frac{x}{y}\ast \frac{y}{rootX}$$ ，即 value[x] = value[x] * value[y]，其中的 y 为未变更之前 x 的父节点。

union() 方法

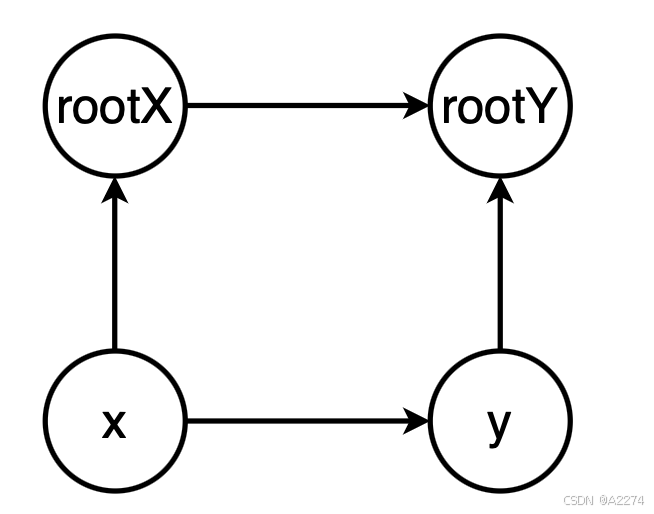
在 union() 方法中，不仅要传递 x, y 的索引，还要传递 value = x / y 的值。先获取 x 和 y 的根节点（获取根节点的时候就让 x, y 指向其根节点 rootX, rootY 了，如下图），如果根节点一样，则直接返回；否则就需要让 rootX 指向 rootY，并更新 rootX 的 value。等式如下：$$\frac{rootX}{rootY}=\frac{y}{rootY}\frac{x}{y}\frac{rootX}{x}$$ ，即有 value[rootX] = value[y] * value / value[x]。

本题还有一个比较麻烦的点：等式中的变量不一定只有一个小写字母。所以需要建立 等式中的变量（以下称作 操作元）与 其在并查集中的索引 的映射，具体请看代码。

query() 方法

由于需要查询某两个操作元之间的比值，还需要在并查集中实现一个方法 query()，如果两个操作元对应的索引在并查集中不连通，则返回 -1；否则返回比值 value[x] / value[y]。等式如下（如果 x, y 连通，则其根节点相同，假设为 root）：$$\frac{x}{y}=\frac{x}{root}\frac{root}{y}$$ ，即 x / y = value[x] / value[y]。

代码

class Solution {
    public double[] calcEquation(List<List<String>> equations,
    							double[] values, List<List<String>> queries) {
        // 先初始化并查集
        init(equations, values);

        // 再进行查询
        int queriesSize = queries.size();
        double[] res = new double[queriesSize];
        for (int i = 0; i < queriesSize; i++) {
            List<String> query = queries.get(i);
            String operand1 = query.get(0); // 操作元1
            String operand2 = query.get(1); // 操作元2
            Integer idx1 = indexMapper.get(operand1); // 操作元1的索引
            Integer idx2 = indexMapper.get(operand2); // 操作元2的索引
            if (idx1 == null || idx2 == null) { // 如果两个操作元有一个找不到
                res[i] = -1; // 则本此查询返回 -1
            } else { // 否则查询 value[idx1] / value[idx2] 的结果
                res[i] = uf.query(idx1, idx2);
            }
        }
        return res;
    }

    private UnionFind uf; // 并查集
    private Map<String, Integer> indexMapper; // 操作元 与 其在并查集中的索引 的映射

    // 初始化并查集
    private void init(List<List<String>> equations, double[] values) {
        int equationsSize = equations.size(); // 获取等式的数量
        uf = new UnionFind(2 * equationsSize); // 创建一个等式数量二倍大小的并查集
        indexMapper = new HashMap<>(2 * equationsSize);
        int idx = 0; // 操作元在并查集中的索引
        for (int i = 0; i < equationsSize; i++) {
        	// 取出每个等式，建立 操作元 与 其在并查集中的索引 的关系
            List<String> equation = equations.get(i);
            String operand1 = equation.get(0); // 操作元1
            String operand2 = equation.get(1); // 操作元2
            if (!indexMapper.containsKey(operand1)) { // 如果 索引映射 中不存在 操作元
                indexMapper.put(operand1, idx++); // 则为其建立映射
            }
            if (!indexMapper.containsKey(operand2)) { // 如果 索引映射 中不存在 操作元
                indexMapper.put(operand2, idx++); // 则为其建立映射
            }
            uf.union(indexMapper.get(operand1), indexMapper.get(operand2), values[i]);
        }
    }

    private static class UnionFind {
        private final int[] parent; // parent[i] 表示 第 i 个元素的父节点
        private final double[] value; // value[i] 表示 第 i 个元素 / 其父节点 的商

        // 初始化并查集
        public UnionFind(int size) {
            parent = new int[size];
            value = new double[size];
            for (int i = 0; i < size; i++) {
                parent[i] = i; // 初始时，每个元素的父节点都是 自己
                value[i] = 1; // 初始时，每个元素与自己的商都是 1
            }
        }

        // 查找 x 的根节点，使用了路径压缩
        public int find(int x) {
            if (x != parent[x]) { // 如果 x 不是根节点
                int temp = parent[x]; // 保存 x 的父节点
                parent[x] = find(parent[x]); // 寻找 x 的根节点
                value[x] *= value[temp]; // 给 本节点与父节点的商 乘 父节点与父节点的父节点的商
            }
            return parent[x]; // 否则返回 parent[x]
        }

        // 合并两个节点所在的集合
        public void union(int x, int y, double value) {
            int rootX = find(x); // x 的根节点
            int rootY = find(y); // y 的根节点
            if (rootX == rootY) {
                return;
            }

            parent[rootX] = rootY; // 让 x 的根节点 指向 y 的根节点，y 的根节点 成为 父节点
            value[rootX] = value[y] * value / value[x];
        }

        // 查询 value[x] / value[y] 的结果
        public double query(int x, int y) {
            if (find(x) == find(y)) { // 如果连通
                return value[x] / value[y]; // 则返回比值
            } else { // 否则不连通
                return -1; // 返回 -1
            }
        }
    }
}