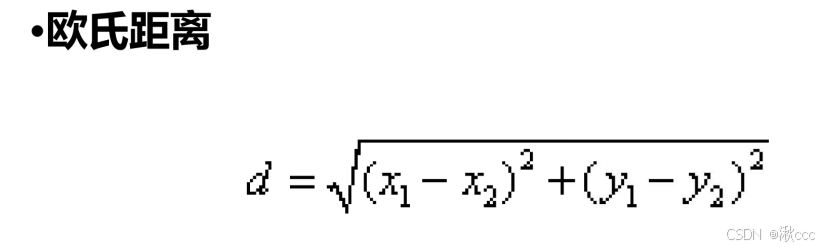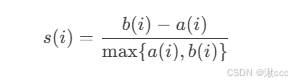目录
一、简介
K-means聚类是一种无监督学习算法,用于将数据集划分为K个簇。其目标是将数据点分配到K个簇中,使得每个簇内的数据点尽可能相似,而不同簇之间的数据点尽可能不同。算法通过迭代更新簇中心和分配数据点,直到簇中心稳定。K-means简单高效,但需要预先指定K值,且对初始质心选择和噪声敏感。广泛应用于图像分割、市场细分等领域。
二、K-means聚类实现步骤
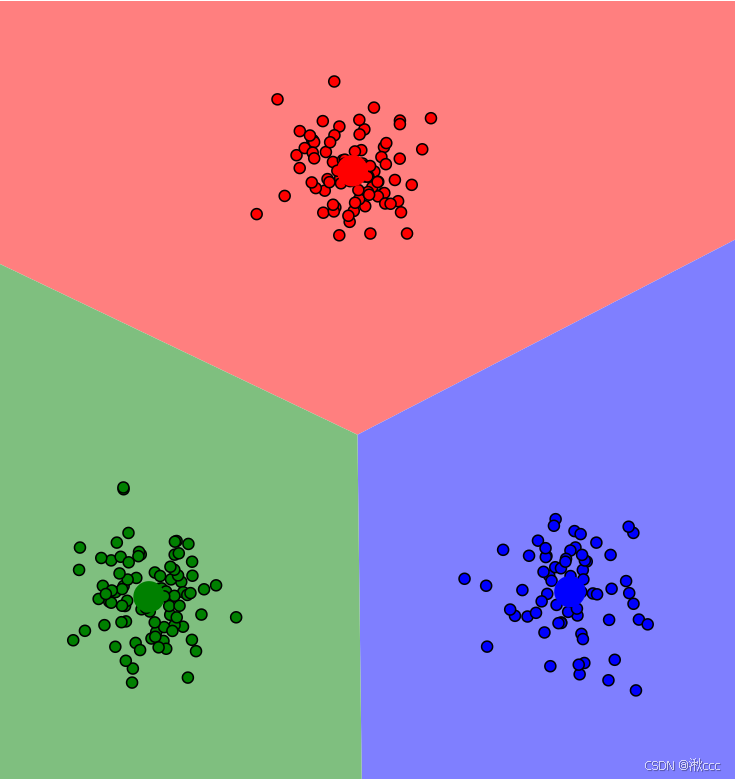
K-means的目标是将数据集划分为K个簇,使得每个簇内的数据点尽可能相似(簇内距离最小),而不同簇之间的数据点尽可能不同(簇间距离最大)。通过迭代优化簇中心和数据点的分配,最终达到簇内方差最小化的目标。
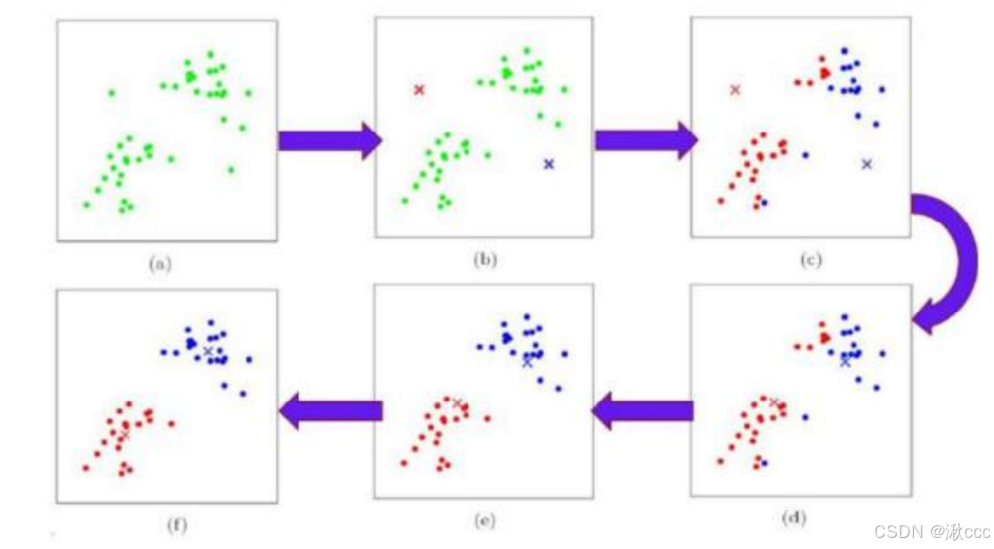
1、初始化数据点、确定K值
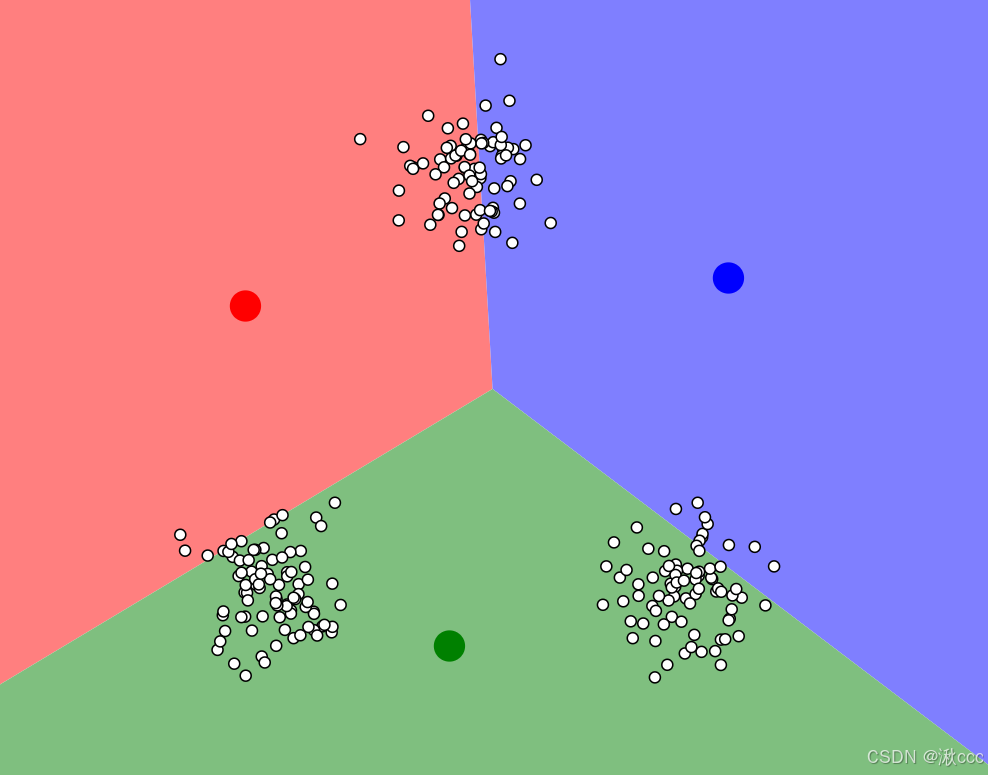
2、通过距离分配数据点
- 计算每个数据点到所有簇中心的距离(通常使用欧几里得距离)。
- 将每个数据点分配到距离最近的簇中心所在的簇。
3、更新簇中心
对每个簇重新计算簇中心,即该簇中所有数据点的坐标平均值
4、 迭代更新
重复2、3两步骤知道簇中心不在发生显著变化或者达到预期迭代次数为止。
推荐一个网站可以直观的观察到K-means算法的演化过程:https://www.naftaliharris.com/blog/visualizing-k-means-clustering/
三、聚类效果评价方式
K-means聚类通过轮廓系数来评判模型聚类效果的好坏。
轮廓系数(Silhouette Coefficient)是一种用于评估聚类效果的指标,衡量数据点在簇内的紧密性和簇间的分离性。它适用于无监督学习中的聚类算法(如K-means、层次聚类等),帮助确定最佳的簇数量(K值)。
1、轮廓系数的定义
对于每个数据点 ii,轮廓系数 s(i)s(i) 的计算公式为:
其中:
-
a(i):数据点 ii 到同簇其他点的平均距离,反映簇内紧密性。
-
b(i):数据点 ii 到最近其他簇中所有点的平均距离,反映簇间分离性。
轮廓系数的取值范围为 [−1,1]:
-
接近 1:表示聚类效果好,数据点与同簇点紧密,且远离其他簇。
-
接近 0:表示数据点处于簇边界,聚类效果不明显。
-
接近 -1:表示数据点可能被分配到错误的簇。
2、整体轮廓系数
对整个数据集,轮廓系数是所有数据点轮廓系数的平均值:
其中,N 是数据点的总数。
3、使用场景
-
评估聚类效果:通过轮廓系数判断聚类结果的合理性。
-
选择K值:在K-means等算法中,通过比较不同K值对应的轮廓系数,选择最优的簇数量(通常选择轮廓系数最大的K值)。
4、优点
-
直观易懂:取值范围明确,易于解释。
-
无需真实标签:适用于无监督学习。
-
综合性强:同时考虑簇内紧密性和簇间分离性。
5、缺点
-
计算复杂度高:需要计算所有数据点之间的距离,适合中小规模数据集。
-
对簇形状敏感:假设簇是凸形的,对非凸形簇效果较差。
6、代码实现方法
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score
import numpy as np
# 示例数据
X = np.array([[1, 2], [1, 4], [1, 0],
[10, 2], [10, 4], [10, 0]])
# K-means聚类
kmeans = KMeans(n_clusters=2, random_state=0)
labels = kmeans.fit_predict(X)
# 计算轮廓系数
score = silhouette_score(X, labels)
print("Silhouette Score:", score)四、K-means聚类代码实现
1、API接口介绍
class sklearn.cluster.KMeans(n_clusters=8,
init=’kmeans++’, n_init=10, max_iter=300,
tol=0.0001, precompute_distances=’auto’,
verbose=0, random_state=None, copy_x=True,
n_jobs=None, algorithm=’auto’)参数介绍 :
-
n_clusters: 类中心的个数,就是要聚成几类。【默认是8个】
-
init:参初始化的方法,默认为'k-means++'
(1)'k-means++': 用一种特殊的方法选定初始质心从而能加速迭代过程的收敛.
(2) ‘random’: 随机从训练数据中选取初始质心。
(3) 如果传递的是一个ndarray,则应该形如 (n_clusters, n_features) 并给出初始质心。
- n_init: 整形,缺省值=10用不同的质心初始化值运行算法的次数,最终解是在inertia意义下选出的最优结果。
-
max_iter :执行一次k-means算法所进行的最大迭代数。
-
Tol: 与inertia结合来确定收敛条件。
-
precompute_distances:三个可选值,‘auto’,True 或者 False。预计算距离,计算速度更快但占用更多内存。
(1)‘auto’:如果 样本数乘以聚类数大于 12million 的话则不预计算距离。
(2)True:总是预先计算距离。
(3)False:永远不预先计算距离。
- random_state :随机种子
-
copy_x:布尔型,默认值=True,当我们precomputing distances时,将数据中心化会得到更准确的结果。如果把此参数值设为True,则原始数据不会被改变。如果是False,则会直接在原始数据 上做修改并在函数返回值时将其还原。但是在计算过程中由于有对数据均值的加减运算,所以数据返回后,原始数据和计算前可能会有细小差别。
-
algorithm:'auto','full' or 'elkan'.默认为'auto'
full:采用经典的EM算法
elkan:通过使用三角不等式从而更有效,但不支持稀疏数据
auto:数据稀疏选择full模式,数据稠密选择elkan模式
属性介绍:
-
cluster_centers_: 一个n-clusters*n_features的矩阵,表示聚类中心的坐标
-
Labels_:每个点的分类标签。
-
inertia_:float形每个点到其簇的质心的距离之和。
-
n_iter_ : int迭代次数。
2、代码示例
例子介绍
以一个啤酒数据集为例子,根据不同啤酒的不同指标对啤酒进行聚类
代码如下
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn import metrics
# 数据预处理
beer = pd.read_table(r'../data/beer.txt',sep=' ',encoding='utf-8',engine='python')
x = beer[["calories","sodium","alcohol","cost"]]
scores = []
index = []
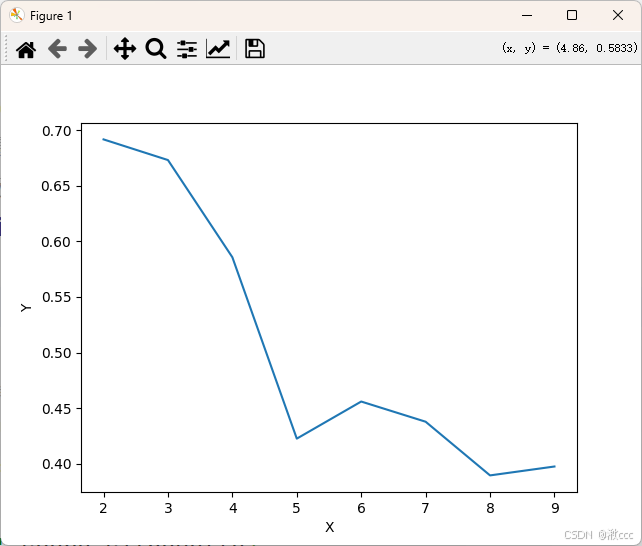
# 交叉验证找到最适合的k值
for k in range(2,10):
labels = KMeans(n_clusters=k).fit(x).labels_
score = metrics.silhouette_score(x,labels)
scores.append(score)
index.append(k)
print(scores)
a = np.argmax(scores)
K = index[a] # 最适合的k值
# k值与轮廓系数的可视化
plt.plot(list(range(2,10)),scores)
plt.xlabel('X')
plt.ylabel('Y')
plt.show()
# 训练、计算轮廓系数
km = KMeans(n_clusters=K).fit(x)
beer['cluster'] = km.labels_
score_silhouette = metrics.silhouette_score(x,beer.cluster)
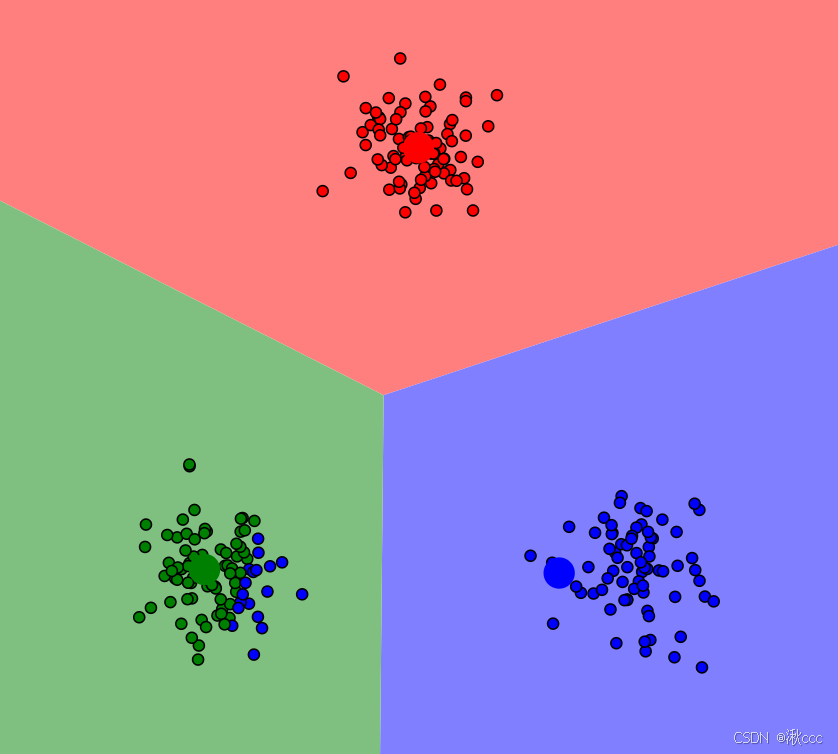
print('轮廓系数:',score_silhouette)结果展示
五、总结
K-means聚类是一种简单而强大的聚类算法,尽管存在一些局限性,但通过合理选择参数和改进方法,仍能在许多实际应用中取得良好效果。对于数据科学家和机器学习从业者来说,掌握K-means聚类是理解无监督学习的重要一步。无论是探索性数据分析还是实际业务场景,K-means都是一种值得信赖的工具。