红黑树的性质

红黑树是一棵二叉搜索树，它的每一个节点都增加了一个存储位来表示颜色（RED、BLACK）。它是为了防止二叉树在特殊情况下退化为链而设计的，可以自己调节节点位置，而不改变搜索顺序，使二叉树能保证在最坏的情况下基本动态集合操作的时间复杂度位O(lg n)。所以红黑树其实就是在二叉搜索树的基础上增加了一些规则。

首先一颗红黑树就是满足下面性质的二叉搜索树：

1. 1. 每一个节点都是红色或者黑色
   2. 根节点是黑色
   3. 每一个叶（NIL）节点是黑色
   4. 红色节点的子节点是黑色
   5. 对于每一个节点，到其后代所有叶节点包含相同多的黑色节点。（黑高相同）

旋转操作

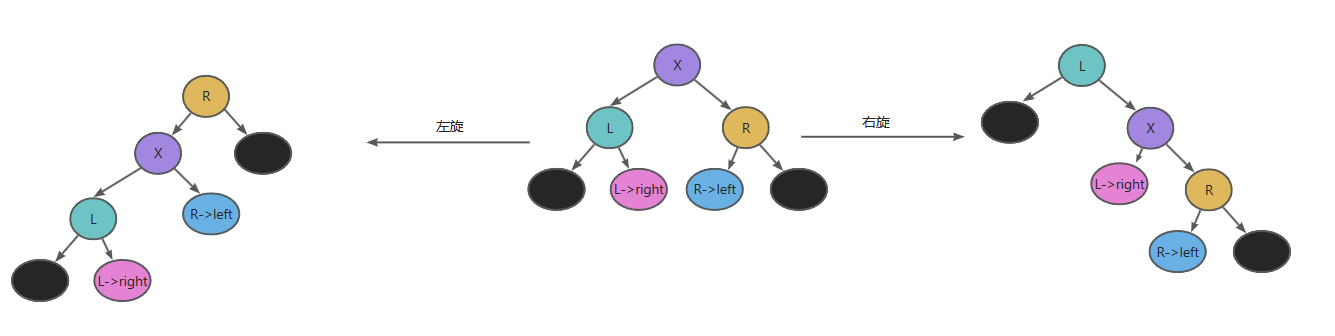
首先对节点X进行旋转操作就是把X以及X的左右子树的一些节点的索引进行修改。

旋转节点X、X左子树L、X右子树R

左旋就是把X放左边，X左子树不变，X左边树变高

右旋就是把X放右边，X右子树不变，X右边树变高

左旋转：

1. 1. X放在原本L位置
   2. R放在原本X位置
   3. L仍然作为X的左子树
   4. R.left作为X.right（因为原本X < R上所有节点，但是 R.left > R ，而且替换之后R.left是X， X.right从原本的R变为了空，所以R.left作为X.right）

右旋转：

1. 1. X放在原本R位置
   2. L放在原本X位置
   3. R仍然为X的右子树
   4. L.right作为X.left（因为原本X > L上所有节点，但是 L . right < R ，而且替换之后L.right是X, X.left 从原本的L变为了空，所以L.right作为X.left）

插入操作

插入节点为N，父节点P，跟节点R，叔节点U，祖父节点G

1. 根节点为空，R = nil

1. 1. N作为根节点，R = N
   2. 颜色为黑色 ，N.color = black

1. 父节点为根节点，P == R

1. 1. X直接插入，N.parent = P
   2. 颜色为黑色，N.color = black

1. 父节点为根节点为根节点而且为红色，p == R && P.color == red

1. 1. X直接插入，N.parent = P
   2. X和P的颜色都为黑色，N.color = black; P.color = block;

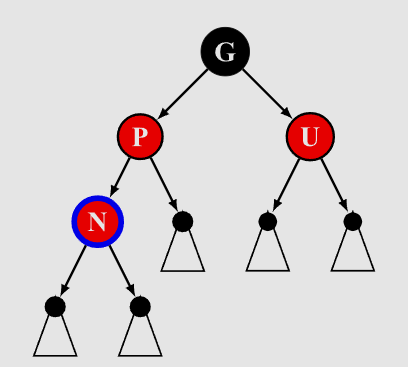
1. 父节点叔节点为红色，P.color == red && U.color == red

如果N为red，那么连续红色，不符合条件

如果N为black，那么P和U的黑高不同，不符合条件

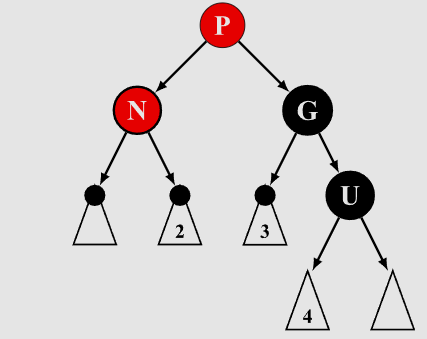
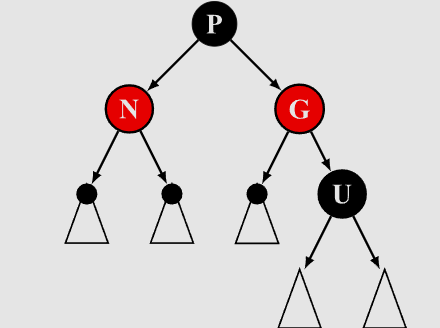
1. 1. N为red，但是把P、U变为black，这样就满足了P、U黑高相等，而且不连红

N.color = red; P.color = black; U.color = black;

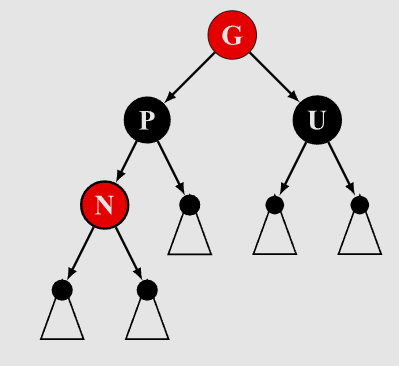
1. 1. 但是G的黑高增加了1，G和G的兄弟黑高不同，将G改为red，此时按照上面办法递归改变颜色就可以了。

、

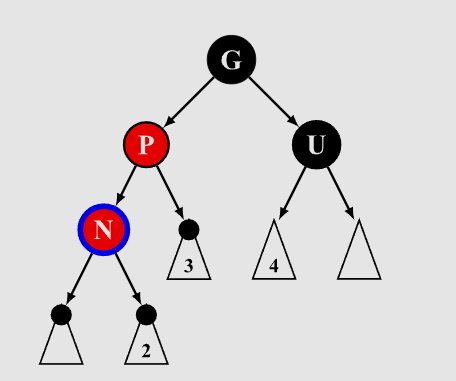
1. N和父节点P方向不同，父节点P和叔节点U颜色不同

((P == G.left && N == P.right) || (P == G.right && N == P.left)) && (P.color != U.color)

此时需要通过旋转为情况6进行操作。

------->

1. N和父节点P方向相同，父节点P和叔节点U颜色不同

((P == G.left && N == P.left) || (P == G.right && N == P.right)) && (P.color != U.color)

此时N若为黑色，则黑高不同，若N为红色，则连红。

先让N为红色，上面说到了通过旋转操作，左旋则左边节点增加，右旋右边节点增加。

1. 1. 若N为P左子树，P就为G左子树，G就不平衡（左边多于右边），对G进行右旋调整高度。（右同理）
   2. 调整之后高度差变为平衡二叉树，所以只需要对其进行从新染色即可。

1. 1. 1. 将P染为黑色P.color = black
      2. 将G染为红色G.color = red

旋转-->

染色-->

删除

被删除节点N,父节点P,左子节点L,右子节点R,叔节点U，兄弟节点B

1. 节点N为叶子节点，L == NIL && R == NIL

1. 1. N为红色N.color == red

1. 1. 1. 直接删除节点N。

1. 1. N为黑色，B为黑色，P为红色N.color == black && B.color == black && P.color == red

1. 1. 1. 删除节点N，将P染色为黑色，B染为红色。（整棵树的黑高没变）

1. 1. N为黑色，B为红色，P为黑色N.color == black && B.color == red && P.color == black

此时删除节点N，N这边黑高短了，P两边的树高相差2，需要旋转减小高度差。（若N=P.left）

1. 1. 1. 将N删掉，对P进行左旋（N的方向），让这棵树是平衡二叉树。
      2. 进行染色。

1. 节点N有一个子节点，N必为红色。(L == NIL && R != NIL)||(L != NIL && R == NIL)

因为N只有一个节点，满足黑高相同的话，那么N只能是黑色，子节点一定是红色。

1. 1. 将N删除，将子节点作为N，并且子节点颜色染为黑色。

1. 节点N有两个子节点。L != NIL && R != NIL

用R最小节点，或L中最大节点，来作为原本的N。然后对这棵树进行旋转调整树高和染色以满足要求。