计算机中的整数有三种2进制表示方法，即原码、反码和补码。

三种表示方法均有符号位和数值位两部分，符号位都是用0表示“正”，用1表示“负”。

正整数的原、反、补码都相同。

负整数的三种表示方法各不相同：

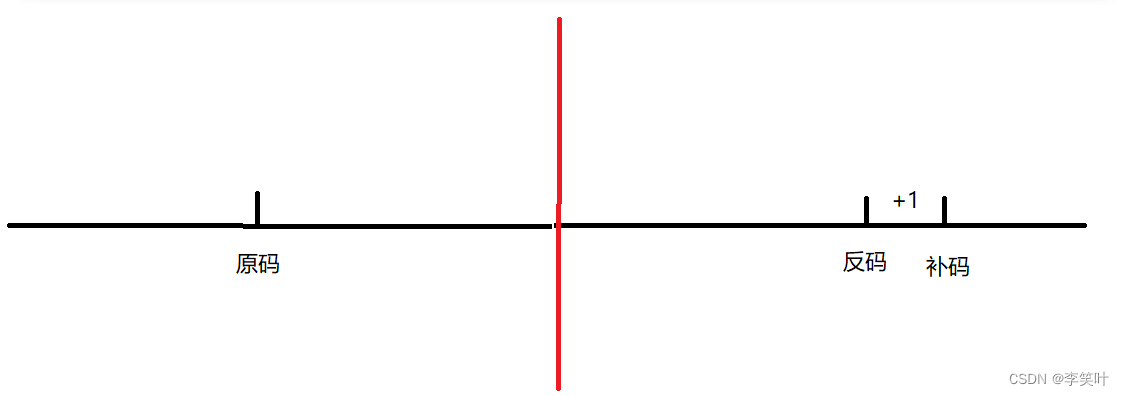
        原码： 直接将数值按照正负数的形式翻译成二进制就可以得到原码。

        反码 ：将原码的符号位不变，其他位依次按位取反就可以得到反码。

        补码 ：反码+1就得到补码。

                                *原码与反码的数值域与此线对称，记住此图便于后续理解。

 对以上概念进行举例说明：

         那么当我们基本了解这个知识后，我们可能会想问，这个知识点有什么用？

一、对于整形来说：数据存在内存中以补码的形式储存。

        如下图：

 上图红框中便是 -10在内存中的储存情况。（2^4=16,所以32位二进制每4位就可以装换位1位十六进制），fffffff6=111111111111111111111111111110110，至于为什么反过来，则涉及到大小端知识点，此处不讲。

二、使用补码，可以将符号位和数值域统一，加法和减法也可以统一处理（CPU只有加法器）

        先举例：

 可以看到使用补码进行计算，得出正确结果。

*然而为什么呢，难道反码就不行吗？为了便于理解，我用数轴来解释这个问题：

可以看到一旦负数的反码在加的过程中会出现1111(全为1的数)，变回原码便是1000，看似是0，实则在数据储存中0应该0000才对。而此时刚好再+1，即可发生位溢出，跳过1111得到0000，这便是补码神奇的地方，使得0只有一种存储形式，即为0000。

*加的过程若没有触及1111，其实反码即可进行计算。

 三、补码与原相互转换，其运算过程是相同的，不需要额外的硬件电路。

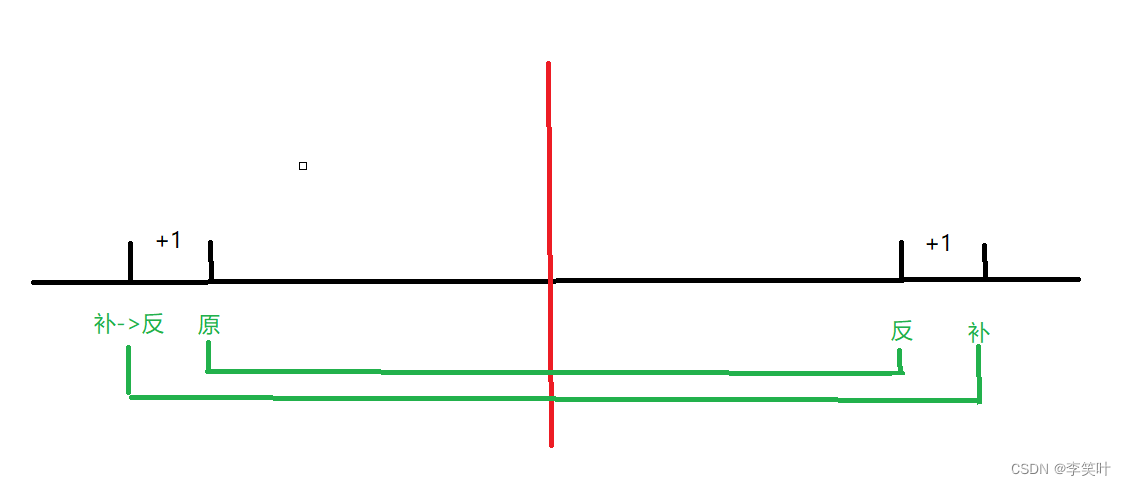
        原码->补码，1种方式，原->反+1->补

        补码->原码，2种方式，补->反+1->原，补-1->反->原

转换利用对称原理，很简单，用开始让记住的图即可轻松理解：

四、总结

        反码是利用对称原理使无论加减法都可以用加法来解决，补码是用来纠正反码加法中可能出现的问题。