文章目录
拟合损失函数
下一篇文章有如何通过损失函数来进行梯度下降法。
一、线性拟合
1.1 介绍
使用最小二乘法进行线性拟合,即,
h
θ
(
x
)
=
θ
0
+
θ
1
x
h_{\theta}(x) = \theta_{0}+\theta_{1}x
hθ(x)=θ0+θ1x
其中,
θ
0
\theta_{0}
θ0和
θ
1
\theta_{1}
θ1是参数,需要通过已经给出的数据进行拟合,这里不进行具体的计算.
损失函数为:
J
(
θ
0
,
θ
1
)
=
1
2
m
∑
i
=
1
m
(
h
θ
(
x
(
i
)
)
−
y
(
i
)
)
2
J(\theta_{0},\theta_{1})=\frac{1}{2m}\sum_{i=1}^{m}(h_{\theta}(x^{(i)})-y^{(i)})^2
J(θ0,θ1)=2m1i=1∑m(hθ(x(i))−y(i))2
即线性拟合的目的即是达到
min
θ
J
(
θ
0
,
θ
1
)
\text{min}_{\theta} J(\theta_{0},\theta_{1})
minθJ(θ0,θ1)
因此我们可以采取梯度下降法进行拟合。
而,不同的 θ 0 \theta_{0} θ0和 θ 1 \theta_{1} θ1获取到不同的损失,我们可以先绘制损失函数的图像,进行参数的预估计。
即,使用matplotlib的三维图像绘制来确定,以及可以使用等高线来进行完成。
1.2 代码可视化
1.2.1 生成示例数据
import numpy as np
import matplotlib.pyplot as plt
# 生成示例数据
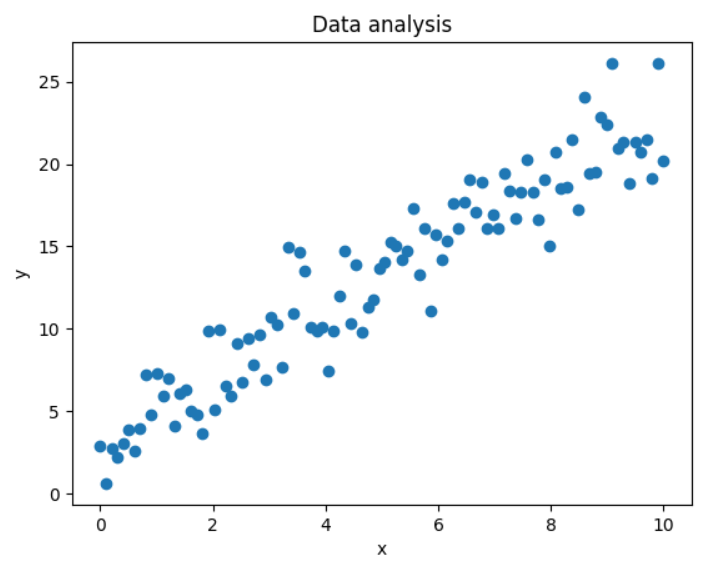
x = np.linspace(0, 10, 100)
y = 2 * x + 3 + np.random.normal(0, 2, 100) # y = 2x + 3 + 噪声
# 绘制散点图,根据散点图大致确定参数范围
plt.scatter(x, y)
plt.title("Data analysis")
plt.xlabel("x")
plt.ylabel("y")
plt.show()
1.2.2 损失函数
def mse_loss(t0, t1, x, y):
# 定义损失函数
y_pred = t1 * x + t0
return np.mean((y - y_pred) ** 2) / 2
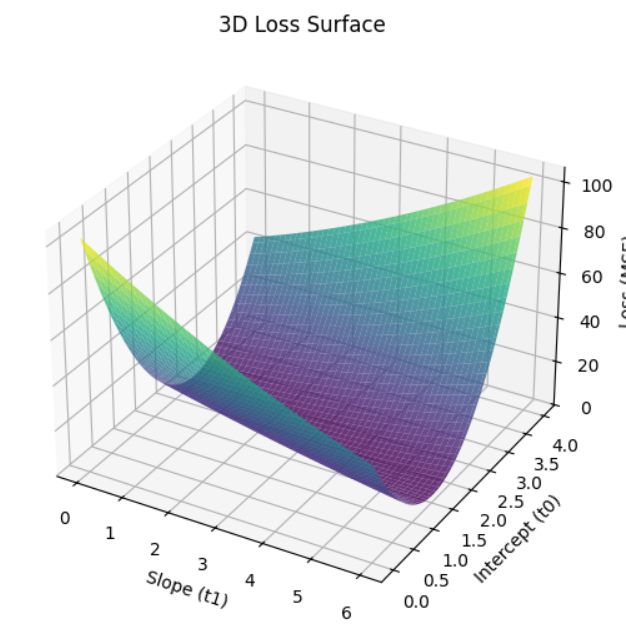
1.2.3 绘制三维图像
t0_, t1_ = np.linspace(0, 6, 100), np.linspace(0, 4, 100) # 定义参数的取值范围
t0, t1 = np.meshgrid(t0_, t1_) # 生成矩阵网格,即形成三维图的x轴和y轴,其为秩一阵
loss = np.zeros_like(t0)
for i in range(t0.shape[0]):
for j in range(t0.shape[1]):
loss[i, j] = mse_loss(t0[i, j],t1[i, j], x, y)
# 绘制三维损失曲面
fig = plt.figure(figsize=(10, 6))
ax = fig.add_subplot(111, projection='3d') # 创建三维坐标系
ax.plot_surface(t0, t1, loss, cmap='viridis', alpha=0.8)
ax.set_xlabel("Slope (t1)")
ax.set_ylabel("Intercept (t0)")
ax.set_zlabel("Loss (MSE)")
ax.set_title("3D Loss Surface")
plt.show()
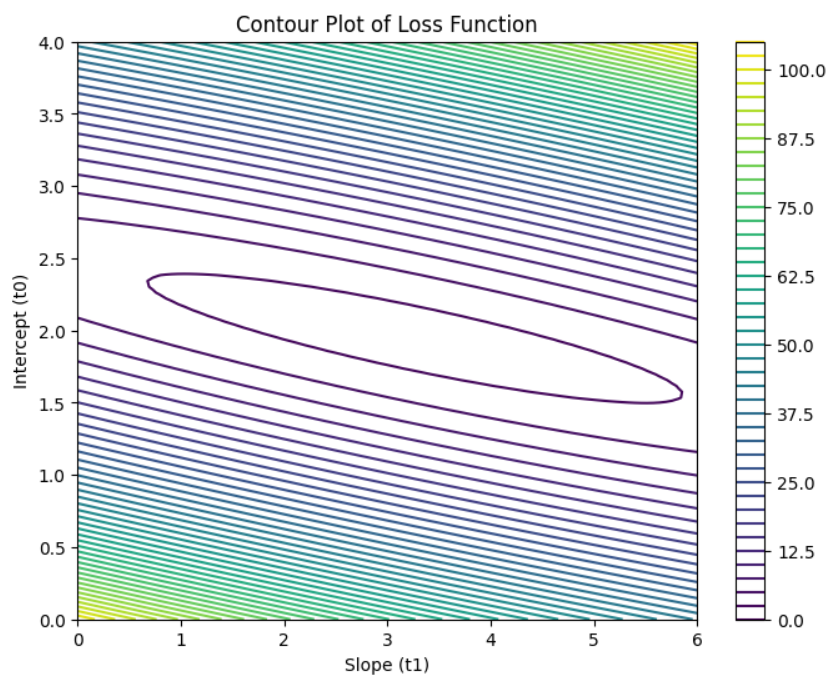
1.2.4 绘制等高线
# 绘制等高线图
plt.figure(figsize=(8, 6))
contour = plt.contour(t0, t1, loss, levels=50, cmap='viridis')
plt.colorbar(contour)
plt.xlabel("Slope (t1)")
plt.ylabel("Intercept (t0)")
plt.title("Contour Plot of Loss Function")
plt.show()
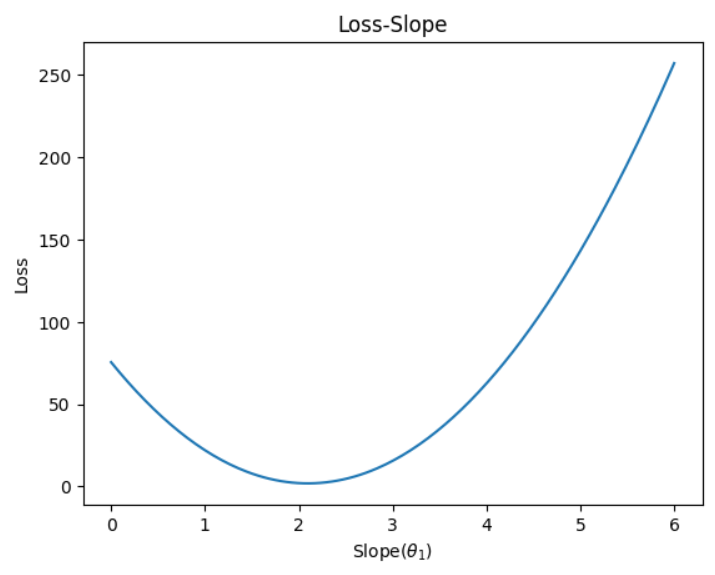
1.2.5 损失函数关于斜率的函数
固定截距,绘制出损失函数关于斜率的图像,通过等高线得出估计的最佳截距。
t1 = np.linspace(0, 6, 200) # 得出斜率的范围
loss = np.zeros_like(t1)
for i in range(loss.shape[0]):
loss[i] = mse_loss(2.5, t1[i], x, y) # 存储损失值
plt.plot(t1, loss)
plt.xlabel(r"Slope($\theta_{1}$)")
plt.ylabel("Loss")
plt.title("Loss-Slope")
plt.show()
通过一系列图像发现,损失值会收敛到一个值
故,可以使用梯度下降法(下一文会介绍)来进行线性拟合求解方程
二、 多变量拟合
2.1 介绍
显然,一个结果会受到多种因素的影响,这时候,就需要引入多项式来进行拟合。需要一些线性代数的知识,小知识。
即,我们令:
y
=
(
x
1
⋯
x
n
1
)
⋅
(
w
1
⋮
w
n
b
)
=
X
W
+
b
=
w
1
x
1
+
⋯
+
w
n
x
n
+
b
\begin{array}{l} y &= \begin{pmatrix} x_1& \cdots& x_n&1 \end{pmatrix}\cdot\begin{pmatrix} w_1\\\vdots\\w_n\\b \end{pmatrix} \\ &= XW+b \\&= w_1x_1+\cdots+w_nx_n+b \end{array}
y=(x1⋯xn1)⋅
w1⋮wnb
=XW+b=w1x1+⋯+wnxn+b
可以看出,使用向量表达,和线性拟合的表达式类似。即,这里使用二项式拟合:
h
θ
(
x
)
(
i
)
=
θ
0
+
θ
1
x
1
(
i
)
+
θ
2
x
2
(
i
)
h
θ
(
x
)
=
(
1
x
1
(
1
)
x
2
(
1
)
⋮
⋮
⋮
1
x
1
(
m
)
x
2
(
m
)
)
m
×
3
⋅
(
θ
0
θ
1
θ
2
)
3
×
1
\begin{array}{l} h_{\theta}(x)^{(i)} &=\theta_{0}+\theta_{1}x_{1}^{(i)}+\theta_{2}x_{2}^{(i)}\\ h_{\theta}(x)&=\begin{pmatrix} 1&x_{1}^{(1)}&x_{2}^{(1)}\\ \vdots&\vdots&\vdots\\ 1&x_{1}^{(m)}&x_{2}^{(m)} \end{pmatrix}_{m\times 3}\cdot\begin{pmatrix} \theta_{0}\\\theta_{1}\\\theta_{2} \end{pmatrix}_{3\times1} \end{array}
hθ(x)(i)hθ(x)=θ0+θ1x1(i)+θ2x2(i)=
1⋮1x1(1)⋮x1(m)x2(1)⋮x2(m)
m×3⋅
θ0θ1θ2
3×1
则,我们的损失函数定义为:
J ( θ 0 , ⋯ , θ n ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 J(\theta_{0},\cdots,\theta_{n}) = \frac{1}{2m}\sum_{i=1}^{m}(h_{\theta}(x^{(i)})-y^{(i)}) ^2 J(θ0,⋯,θn)=2m1i=1∑m(hθ(x(i))−y(i))2
2.2 代码可视化
2.2.1 生成示例数据
import numpy as np
import matplotlib.pyplot as plt
# 这里迭代区间最好不要一样,不然 x1 = x2
x1 = np.linspace(0, 10, 100)
x2 = np.linspace(-10, 0, 100)
y = 2 * x1 + 3 * x2 + 4 + np.random.normal(0, 4, 100) # 生成噪声数据,即生成正态分布的随机数
# 绘制散点图,三维散点图
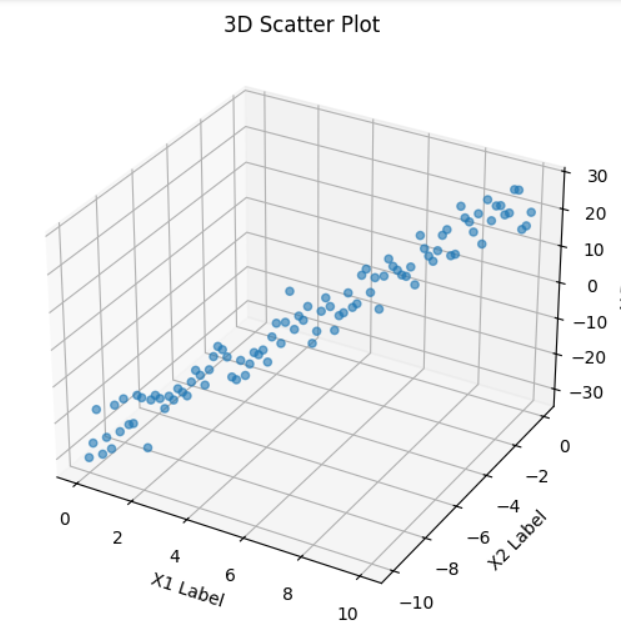
fig = plt.figure(figsize=(10, 6))
ax = fig.add_subplot(111, projection='3d')
# 绘制三维散点图
ax.scatter(x1, x2, y, alpha=0.6)
# 设置坐标轴标签
ax.set_xlabel('X1 Label')
ax.set_ylabel('X2 Label')
ax.set_zlabel('Y Data')
# 设置标题
ax.set_title('3D Scatter Plot')
plt.show()
2.2.2 损失函数
使用点积来进行损失函数的编写:
其实,线性函数也可以用点积来编写,不过运算较为简单,就可以不考虑点积
def mse_loss(para, X, y):
"""
para: nx1 的列向量
x: mxn 的数据矩阵
y: nx1的列向量
"""
y_pre = np.dot(X, para) # 使用点积定义拟合函数
return np.mean((y_pre-y)**2) / 2
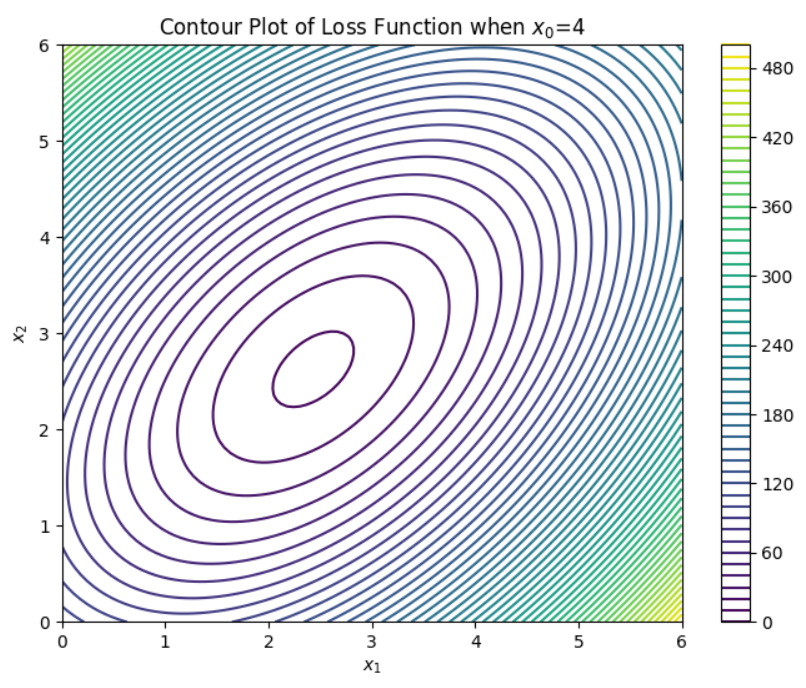
2.2.3 绘制等高线
这里等高线的绘制,先寻找一个大概截距,即固定一个值,而后再进行二维等高线的绘制:
# 对数据进行预处理
one_ = np.ones_like(x1) # 生成一个全为1的列向量
X = np.array([one_, x1, x2]).T # 合成为一个100行三列的数据矩阵
x10, x20 = np.linspace(0, 6, 100), np.linspace(0, 6, 100)
x1_, x2_ = np.meshgrid(x10, x20)
loss = np.zeros_like(x1_)
for i in range(x1_.shape[0]): # 批量计算损失函数
for j in range(x1_.shape[1]):
param = np.array([0, x1_[i][j], x2_[i][j]]) # 假设截距为0
loss[i][j] = mse_loss(param, X, y)
plt.figure(figsize=(8, 6))
contour = plt.contour(x1_, x2_, loss, levels=50, cmap='viridis')
plt.colorbar(contour)
plt.xlabel(r"$x_1$")
plt.ylabel(r"$x_2$")
plt.title(r"Contour Plot of Loss Function when $x_0$=4")
plt.show()
通过等高线的绘制,可以大致确定
x
1
x_{1}
x1和
x
2
x_{2}
x2的估计值,而后使用梯度下降法进行进一步的求解。
三、 多项式拟合
3.1 介绍
在一些拟合过程中其实单变量影响,但是通过散点图很容易发现,其并不是线性函数,因此并不能进行线性拟合,而是要进行多项式拟合,即使用x的多次方的加和形式进行拟合:
f
(
x
)
=
∑
i
=
0
n
a
i
x
i
f(x) = \sum_{i=0}^{n}a_{i}x^{i}
f(x)=i=0∑naixi
同时,也可以使用
y
=
θ
0
+
θ
1
x
+
θ
2
x
y=\theta_{0}+\theta_{1}x+\theta_{2}\sqrt{ x }
y=θ0+θ1x+θ2x来进行拟合。
具体的多项式拟合形式,需要结合其他数据,以及具体情况进行分析。
则,其损失函数为:
min
θ
J
(
θ
)
=
min
θ
1
2
m
∑
i
=
0
m
(
f
(
x
(
i
)
)
−
y
(
i
)
)
2
\text{min}_{\theta} J(\theta)=\text{min}_{\theta}\frac{1}{2m}\sum_{i=0}^{m} (f(x^{(i)})-y^{(i)})^2
minθJ(θ)=minθ2m1i=0∑m(f(x(i))−y(i))2
3.2 公式表示
拟合方式则是与多变量拟合的过程类似(令 φ ( x ) \varphi(x) φ(x)为x的多次方形式)
即
h
θ
(
x
)
=
(
1
φ
1
(
x
(
1
)
)
⋯
φ
n
(
x
(
1
)
)
⋮
⋮
⋱
⋮
1
φ
1
(
x
(
m
)
)
⋯
φ
n
(
x
(
m
)
)
)
m
×
(
n
+
1
)
⋅
(
θ
0
θ
1
⋮
θ
n
)
(
n
+
1
)
×
1
\begin{array}{l} h_{\theta}(x)=\begin{pmatrix} 1&\varphi_1(x^{(1)})&\cdots&\varphi_n(x^{(1)})\\ \vdots&\vdots&\ddots &\vdots\\ 1&\varphi_1(x^{(m)})&\cdots&\varphi_n(x^{(m)}) \end{pmatrix}_{m\times (n+1)}\cdot\begin{pmatrix} \theta_{0}\\\theta_{1}\\\vdots\\\theta_n \end{pmatrix}_{(n+1)\times1} \end{array}
hθ(x)=
1⋮1φ1(x(1))⋮φ1(x(m))⋯⋱⋯φn(x(1))⋮φn(x(m))
m×(n+1)⋅
θ0θ1⋮θn
(n+1)×1
而后进行相似的运算即可绘制出图像。