文章目录
Python 梯度下降法(上)
一、原理
1.1 多元函数
多元函数中的梯度:对于一个多元函数,比如二元函数 z = f ( x , y ) z=f(x,y) z=f(x,y),它的梯度是一个向量。在平面直角坐标系中,梯度向量 ∇ f ( x , y ) = ( ∂ f ∂ x , ∂ f ∂ y ) \nabla f(x,y)=(\frac{\partial f}{\partial x} ,\frac{\partial f}{\partial y} ) ∇f(x,y)=(∂x∂f,∂y∂f)。梯度的方向表示函数在该点处变化最快的方向,而梯度的模(长度)表示函数在该方向上的变化率大小。即,其几何意义为:在函数 z = f ( x , y ) z=f(x,y) z=f(x,y)的图像上,梯度向量是与其等高线(使得函数值为常数的曲线)垂直的向量,并且指向函数值增大的方向。
例如,对于函数 f ( x , y ) = x 2 + y 2 , ∂ f ∂ x = 2 x , ∂ f ∂ y = 2 y f(x, y)=x^2+y^2,\frac{\partial f}{\partial x} =2x,\frac{\partial f}{\partial y}=2y f(x,y)=x2+y2,∂x∂f=2x,∂y∂f=2y,那么其梯度为: ∇ f ( x , y ) = ( 2 x , 2 y ) \nabla f(x,y)=(2x,2y) ∇f(x,y)=(2x,2y),即函数沿着x轴的变化率为 2 x 2x 2x,函数沿着y轴的变化率为 2 y 2y 2y。
1.2 梯度下降法
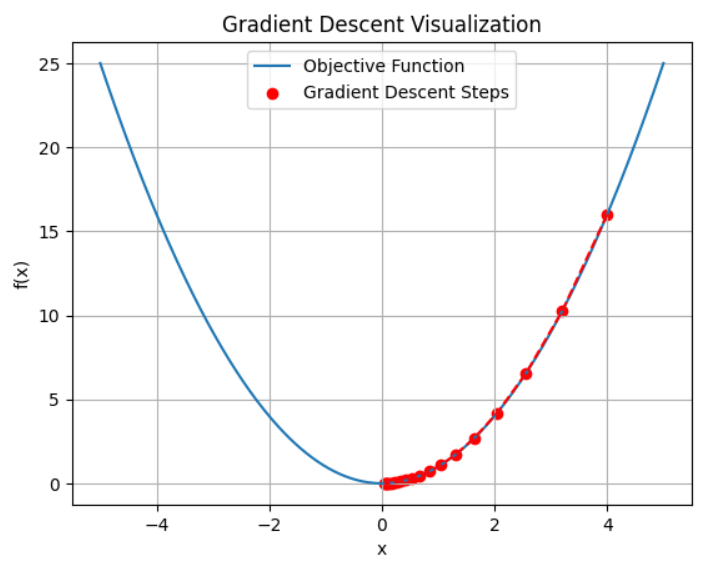
在机器学习过程中,训练模型通过需要最小化损失函数 J ( θ ) J(\theta) J(θ),来进行模型的训练。梯度下降算法就是利用损失函数对参数的梯度来更新参数,使得损失函数值不断减小,也即: θ t + 1 = θ t − α ∇ J ( θ t ) \theta_{t+1}=\theta_{t}-\alpha\nabla J(\theta_{t}) θt+1=θt−α∇J(θt)。这里有一个使用梯度下降法寻找极值的例子。
import numpy as np
import matplotlib.pyplot as plt
# 定义目标函数
objective_function = lambda x: x**2
# 定义目标函数的导数
gradient = lambda x: 2 * x
# 梯度下降函数
def gradient_descent(initial_x, learning_rate, num_iterations):
x_values = [initial_x]
y_values = [objective_function(initial_x)]
x = initial_x
num_iterations = 0
grad = gradient(x)
while not (abs(grad <= 1e-5)): # 当梯度小于一定的值时,就代表取得极值
num_iterations += 1
# 更新 x
x = x - learning_rate * grad
# 记录更新后的 x 和对应的函数值
x_values.append(x)
y_values.append(objective_function(x))
# 计算梯度
grad = gradient(x)
return x_values, y_values, num_iterations
# 初始化参数
initial_x = 4
learning_rate = 0.1
num_iterations = 20
# 执行梯度下降
x_values, y_values, num_iterations = gradient_descent(initial_x, learning_rate, num_iterations)
# 绘制目标函数曲线
x = np.linspace(-5, 5, 400)
y = objective_function(x)
plt.plot(x, y, label='Objective Function')
# 绘制梯度下降过程
plt.scatter(x_values, y_values, color='red', label='Gradient Descent Steps')
plt.plot(x_values, y_values, color='red', linestyle='--')
# 设置图形属性
plt.title('Gradient Descent Visualization')
plt.xlabel('x')
plt.ylabel('f(x)')
plt.legend()
plt.grid(True)
plt.show()
二、常见的梯度公式
矩阵求导工具,可以使用网站:Matrix Calculus
2.1 标量对向量的梯度
设 X = ( x 1 , x 2 , ⋯ , x n ) T X=(x_1,x_2,\cdots,x_n)^T X=(x1,x2,⋯,xn)T是一个n维向量, f ( x ) f(x) f(x)是一个关于X的标量函数,即 f : R n ⇒ R f: \mathbb{R}^n\Rightarrow \mathbb{R} f:Rn⇒R。
标量函数 f ( x ) f(x) f(x)对向量X的梯度是一个n维向量,其第i个分量是f关于 x i x_i xi的偏导数,即为 ∇ X f ( X ) \nabla_{X} f(X) ∇Xf(X)或 ∂ f ∂ X \frac{\partial f}{\partial X} ∂X∂f具体形式为:
∇ X f ( X ) = ( ∂ y ∂ x 1 ∂ y ∂ x 2 ⋮ ∂ y ∂ x n ) \nabla_{X} f(X)=\begin{pmatrix} \frac{\partial y}{\partial x_1} \\ \frac{\partial y}{\partial x_2} \\ \vdots \\ \frac{\partial y}{\partial x_n} \end{pmatrix} ∇Xf(X)= ∂x1∂y∂x2∂y⋮∂xn∂y
如,二次型 f ( X ) = X T X = ∑ i = 1 n x i 2 f(X)=X^TX=\sum_{i=1}^nx_{i}^2 f(X)=XTX=∑i=1nxi2,根据偏导数的计算规则, ∂ f ∂ x i = 2 x i \frac{\partial f}{\partial x_{i}}=2x_{i} ∂xi∂f=2xi, ∇ X f ( X ) = 2 X \nabla_{X} f(X)=2X ∇Xf(X)=2X
2.2 向量对向量的梯度
设 f ( x ) = ( f 1 ( x ) f 2 ( x ) ⋯ f m ( x ) ) T f(x)=\begin{pmatrix}f_1(x) &f_2(x)&\cdots&f_m(x)\end{pmatrix}^T f(x)=(f1(x)f2(x)⋯fm(x))T是一个m维向量函数,其中 X = ( x 1 , x 2 , ⋯ , x n ) T X=(x_1,x_2,\cdots,x_n)^T X=(x1,x2,⋯,xn)T是n维向量,即 f : R n ⇒ R m f: \mathbb{R}^n\Rightarrow \mathbb{R}^m f:Rn⇒Rm。
向量函数
f
(
X
)
f(X)
f(X)对向量
X
X
X的梯度是一个
m
×
n
m\times n
m×n矩阵,将其称为雅克比矩阵(Jacobian matrix)。记为
J
f
(
X
)
J_{f(X)}
Jf(X)或
∂
f
∂
X
\frac{\partial f}{\partial X}
∂X∂f,其元素为:
J
f
(
X
)
=
(
∂
f
1
∂
x
1
∂
f
1
∂
x
2
⋯
∂
f
1
∂
x
n
∂
f
2
∂
x
1
∂
f
2
∂
x
2
⋯
∂
f
2
∂
x
n
⋮
⋮
⋱
⋮
∂
f
m
∂
x
1
∂
f
m
∂
x
2
⋯
∂
f
m
∂
x
n
)
J_{f(X)}=\begin{pmatrix} \frac{\partial f_1}{\partial x_1} & \frac{\partial f_1}{\partial x_2} & \cdots & \frac{\partial f_1}{\partial x_n}\\ \frac{\partial f_2}{\partial x_1} & \frac{\partial f_2}{\partial x_2} & \cdots & \frac{\partial f_2}{\partial x_n}\\ \vdots& \vdots & \ddots &\vdots \\ \frac{\partial f_m}{\partial x_1} & \frac{\partial f_m}{\partial x_2} & \cdots & \frac{\partial f_m}{\partial x_n}\\ \end{pmatrix}
Jf(X)=
∂x1∂f1∂x1∂f2⋮∂x1∂fm∂x2∂f1∂x2∂f2⋮∂x2∂fm⋯⋯⋱⋯∂xn∂f1∂xn∂f2⋮∂xn∂fm
例如,设
X
=
(
x
1
,
x
2
)
T
,
f
(
x
)
=
[
f
1
(
x
)
,
f
2
(
x
)
]
T
=
[
x
1
2
+
x
2
,
x
1
x
2
2
]
T
X=(x_{1},x_{2})^T,f(x)=[f_{1}(x),f_{2}(x)]^T=[x_{1^2}+x_{2},x_{1}x_{2}^2]^T
X=(x1,x2)T,f(x)=[f1(x),f2(x)]T=[x12+x2,x1x22]T
计算偏导数所形成的雅克比矩阵:
J
f
(
X
)
=
(
2
x
1
1
x
2
2
2
x
1
x
2
)
J_{f(X)}=\begin{pmatrix} 2x_1&1\\ x_2^2&2x_1x_2 \end{pmatrix}
Jf(X)=(2x1x2212x1x2)
2.3 向量对标量的梯度
设 f ( x ) = ( f 1 ( x ) f 2 ( x ) ⋯ f m ( x ) ) T f(x)=\begin{pmatrix}f_1(x) &f_2(x)&\cdots&f_m(x)\end{pmatrix}^T f(x)=(f1(x)f2(x)⋯fm(x))T是一个n维向量, x x x是一个标量,即 f : R ⇒ R n f: \mathbb{R}\Rightarrow \mathbb{R}^n f:R⇒Rn。
向量
f
(
x
)
f(x)
f(x)对标量
x
x
x的梯度是一个n维向量,它的每个分量是向量
f
(
x
)
f(x)
f(x)中对应元素关于标量
x
x
x的导数,记为
d
f
d
x
\frac{d\textbf{f}}{dx}
dxdf,即:
∇
x
f
(
x
)
=
d
f
d
x
=
(
d
y
1
d
x
d
y
2
d
x
⋮
d
y
n
d
x
)
\nabla_xf(x)=\frac{d\textbf{f} }{dx}=\begin{pmatrix} \frac{dy_1}{dx}\\ \frac{dy_2}{dx} \\ \vdots\\ \frac{dy_n}{dx} \end{pmatrix}
∇xf(x)=dxdf=
dxdy1dxdy2⋮dxdyn
2.4 标量对矩阵的梯度
设 X = ( x i j ) m × n X=(x_{ij})_{m\times n} X=(xij)m×n是一个 m × n m\times n m×n的矩阵, f ( X ) f(X) f(X)是一个关于 X X X的标量函数,即 f : R m × n ⇒ R f:\mathbb{R}^{m\times n}\Rightarrow \mathbb{R} f:Rm×n⇒R。
标量函数
f
(
X
)
f(X)
f(X)对矩阵
X
X
X的梯度是一个
m
×
n
m\times n
m×n的矩阵,其
(
i
,
j
)
(i,j)
(i,j)位置的元素是
f
f
f关于
x
i
j
x_{ij}
xij的偏导数,记为
∇
X
f
(
X
)
\nabla_{X} f(X)
∇Xf(X)或
∂
f
∂
X
\frac{\partial f}{\partial X}
∂X∂f,即:
(
∇
X
f
(
X
)
)
i
j
=
∂
f
∂
x
i
j
(\nabla_{X} f(X))_{ij}=\frac{\partial f}{\partial x_{ij}}
(∇Xf(X))ij=∂xij∂f
三、常见梯度算法
3.1 Batch Gradient Descent
3.1.1 数学原理
批量梯度下降(Batch Gradient Descent,BGD)是一种用于优化目标函数的迭代算法,常用于机器学习中训练模型,特别是在线性回归、逻辑回归等算法里寻找最优参数。其核心思想是在每次迭代时,使用训练数据集中的所有样本计算目标函数的梯度,然后沿着梯度的反方向更新模型参数,逐步使目标函数达到最小值。
假设我们有m个样本的训练数据集: { ( x ( 1 ) , y ( 1 ) ) , ( x ( 2 ) , y ( 2 ) ) , ⋯ , ( x ( i ) , y ( i ) ) , ⋯ , ( x ( m ) , y ( m ) ) } \{(x^{(1)},y^{(1)}),(x^{(2)},y^{(2)}),\cdots,(x^{(i)},y^{(i)}),\cdots,(x^{(m)},y^{(m)}) \} {(x(1),y(1)),(x(2),y(2)),⋯,(x(i),y(i)),⋯,(x(m),y(m))},目标是最小化一个损失函数 J ( θ ) J(\theta) J(θ),其中 θ \theta θ是模型的参数向量。
J ( θ ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 J(\theta)=\frac{1}{2m}\sum_{i=1}^m(h_{\theta}(x^{(i)})-y^{(i)})^2 J(θ)=2m1∑i=1m(hθ(x(i))−y(i))2
而损失函数的梯度为:
∇
θ
J
(
θ
)
=
1
2
m
∑
i
=
1
m
∇
θ
(
h
θ
(
x
(
i
)
)
−
y
(
i
)
)
2
=
1
m
∑
i
=
1
m
(
h
θ
(
x
(
i
)
)
−
y
(
i
)
)
∇
θ
h
θ
(
x
(
i
)
则:
∂
J
(
θ
)
∂
θ
j
=
1
m
∑
i
=
1
m
(
h
θ
(
x
(
i
)
)
−
y
(
i
)
)
x
j
(
i
)
∇
θ
J
(
θ
)
=
1
m
X
T
(
h
θ
(
X
)
−
y
)
\begin{array}{l} \nabla_{\theta}J(\theta)&=\frac{1}{2m}\sum_{i=1}^{m}\nabla_{\theta}(h_{\theta}(x^{(i)})-y^{(i)})^2 \\ &=\frac{1}{m}\sum_{i=1}^{m}(h_{\theta}(x^{(i)})-y^{(i)})\nabla_{\theta}h_{\theta}(x^{(i)} \\ 则:\frac{\partial J(\theta)}{\partial \theta_{j}}&=\frac{1}{m}\sum_{i=1}^{m}(h_{\theta}(x^{(i)})-y^{(i)})x_{j}^{(i)} \\ \nabla_{\theta}J(\theta)&=\frac{1}{m}X^T(h_{\theta}(X)-y) \\ \end{array}
∇θJ(θ)则:∂θj∂J(θ)∇θJ(θ)=2m1∑i=1m∇θ(hθ(x(i))−y(i))2=m1∑i=1m(hθ(x(i))−y(i))∇θhθ(x(i)=m1∑i=1m(hθ(x(i))−y(i))xj(i)=m1XT(hθ(X)−y)
然后根据梯度更新参数:
θ
i
+
1
=
θ
i
−
α
∇
θ
J
(
θ
)
\theta_{i+1}=\theta_{i}-\alpha \nabla_{\theta}J(\theta)
θi+1=θi−α∇θJ(θ)。其中
α
\alpha
α是学习率,控制每次参数更新的步长,这个参数如何选择后文讲述。
对于拟合,假设有n个参数,m组数据:
X
X
X为
m
×
n
m\times n
m×n矩阵,
(
h
θ
(
X
)
−
y
)
(h_{\theta}(X)-y)
(hθ(X)−y)是
m
×
1
m\times 1
m×1的矩阵,则
∇
θ
J
(
θ
)
\nabla_{\theta}J(\theta)
∇θJ(θ)为
n
×
1
n\times 1
n×1矩阵,要注意
θ
\theta
θ的维度为
n
×
1
n\times 1
n×1。
3.1.2 代码实现
# 定义批量梯度下降函数
def batch_gradient_descent(X, y, alpha, num_iterations):
m, n = X.shape
theta = np.zeros((n, 1)) # 初始化参数
loss_ = []
for iteration in range(num_iterations):
# 计算预测值
h = np.dot(X, theta)
# 计算误差
error = h - y
loss_.append(np.mean(error**2) / 2)
# 计算梯度
gradient = (1/m) * np.dot(X.T, error)
# 更新参数
theta = theta - alpha * gradient
return theta.reshape(2), loss_
总代码:
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['Microsoft YaHei']
# 定义批量梯度下降函数
def batch_gradient_descent(X, y, alpha, num_iterations):
m, n = X.shape
theta = np.zeros((n, 1)) # 初始化参数
loss_ = []
for iteration in range(num_iterations):
# 计算预测值
h = np.dot(X, theta)
# 计算误差
error = h - y
loss_.append(np.mean(error**2) / 2)
# 计算梯度
gradient = (1/m) * np.dot(X.T, error)
# 更新参数
theta = theta - alpha * gradient
return theta.reshape(2), loss_
# 生成一些示例数据
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)
# 添加偏置项
X_b = np.c_[np.ones((100, 1)), X]
# 设置超参数
alpha = 0.1 # 这个
num_iterations = 1000
# 执行批量梯度下降
theta, loss_ = batch_gradient_descent(X_b, y, alpha, num_iterations)
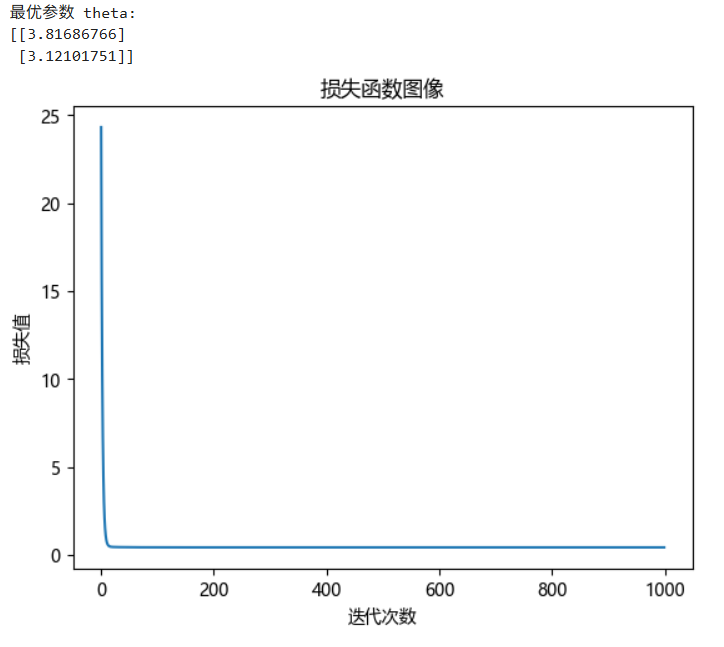
print("最优参数 theta:")
print(theta)
plt.plot(range(len(loss_)), loss_, label="损失函数图像")
plt.title("损失函数图像")
plt.xlabel("迭代次数")
plt.ylabel("损失值")
plt.show()
发现在多次迭代后,最后损失值收敛。梯度下降法可以达到局部最优,有时并不可以达到全局的最优解。
3.1.3 优缺点
- 优点:
- 由于使用了所有样本的信息,梯度的计算相对稳定,能够保证收敛到全局最优解(对于凸函数)。
- 最终得到的模型参数精度较高。
- 缺点:
- 每次迭代都需要遍历整个数据集,计算量较大,尤其是当数据集规模非常大时,训练速度会非常慢。
- 内存需求较高,因为需要同时存储所有样本的数据。
3.2 Stochastic Gradient Descent
3.2.1 数学原理
随机梯度下降(Stochastic Gradient Descent,SGD)是一种用于优化目标函数的迭代算法,常用于机器学习模型的训练,特别是在处理大规模数据集时表现出色。与批量梯度下降(Batch Gradient Descent)每次迭代使用整个数据集计算梯度不同,随机梯度下降每次迭代只随机选择一个样本计算梯度,并根据该梯度更新模型参数。
随机梯度下降法的数学原理和批量梯度下降法的数学原理是一样的。但是,随机梯度下降法,每次迭代只使用一个样本数据来更新参数。这样在数据量很大的情况下,计算量相对较小,算法运行速度快。但由于每次更新仅基于一个样本,可能会导致参数更新方向波动较大,不太稳定。
假设我们有m个样本的训练数据集: { ( x ( 1 ) , y ( 1 ) ) , ( x ( 2 ) , y ( 2 ) ) , ⋯ , ( x ( i ) , y ( i ) ) , ⋯ , ( x ( m ) , y ( m ) ) } \{(x^{(1)},y^{(1)}),(x^{(2)},y^{(2)}),\cdots,(x^{(i)},y^{(i)}),\cdots,(x^{(m)},y^{(m)}) \} {(x(1),y(1)),(x(2),y(2)),⋯,(x(i),y(i)),⋯,(x(m),y(m))},目标是最小化一个损失函数 J ( θ ) J(\theta) J(θ),其中 θ \theta θ是模型的参数向量。
J ( θ ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 J(\theta)=\frac{1}{2m}\sum_{i=1}^m(h_{\theta}(x^{(i)})-y^{(i)})^2 J(θ)=2m1∑i=1m(hθ(x(i))−y(i))2
而损失函数的梯度为:
∇
θ
J
(
θ
)
=
1
2
m
∑
i
=
1
m
∇
θ
(
h
θ
(
x
(
i
)
)
−
y
(
i
)
)
2
=
1
m
∑
i
=
1
m
(
h
θ
(
x
(
i
)
)
−
y
(
i
)
)
∇
θ
h
θ
(
x
(
i
)
则:
∂
J
(
θ
)
∂
θ
j
=
1
m
∑
i
=
1
m
(
h
θ
(
x
(
i
)
)
−
y
(
i
)
)
x
j
(
i
)
∇
θ
J
(
θ
)
=
1
m
X
T
(
h
θ
(
X
)
−
y
)
\begin{array}{l} \nabla_{\theta}J(\theta)&=\frac{1}{2m}\sum_{i=1}^{m}\nabla_{\theta}(h_{\theta}(x^{(i)})-y^{(i)})^2 \\ &=\frac{1}{m}\sum_{i=1}^{m}(h_{\theta}(x^{(i)})-y^{(i)})\nabla_{\theta}h_{\theta}(x^{(i)} \\ 则:\frac{\partial J(\theta)}{\partial \theta_{j}}&=\frac{1}{m}\sum_{i=1}^{m}(h_{\theta}(x^{(i)})-y^{(i)})x_{j}^{(i)} \\ \nabla_{\theta}J(\theta)&=\frac{1}{m}X^T(h_{\theta}(X)-y) \\ \end{array}
∇θJ(θ)则:∂θj∂J(θ)∇θJ(θ)=2m1∑i=1m∇θ(hθ(x(i))−y(i))2=m1∑i=1m(hθ(x(i))−y(i))∇θhθ(x(i)=m1∑i=1m(hθ(x(i))−y(i))xj(i)=m1XT(hθ(X)−y)
然后根据梯度更新参数:
θ
i
+
1
=
θ
i
−
α
∇
θ
J
(
θ
)
\theta_{i+1}=\theta_{i}-\alpha \nabla_{\theta}J(\theta)
θi+1=θi−α∇θJ(θ)。其中
α
\alpha
α是学习率,控制每次参数更新的步长,这个参数如何选择后文讲述。
对于拟合,假设有n个参数,m组数据:
X
X
X为
m
×
n
m\times n
m×n矩阵,
(
h
θ
(
X
)
−
y
)
(h_{\theta}(X)-y)
(hθ(X)−y)是
m
×
1
m\times 1
m×1的矩阵,则
∇
θ
J
(
θ
)
\nabla_{\theta}J(\theta)
∇θJ(θ)为
n
×
1
n\times 1
n×1矩阵,要注意
θ
\theta
θ的维度为
n
×
1
n\times 1
n×1。
3.2.2 代码实现
实现函数:
# 定义随机梯度下降函数
def stochastic_gradient_descent(X, y, alpha, num_iter):
m, n = X.shape
theta = np.random.randn(n, 1) # 随机初始化参数
loss_ = [] # 定义一个空列表,进行损失数据的存储
for _ in range(num_iter):
for i in range(m):
# 随机选择一个样本,即只使用一个数据进行拟合,找到最优解
random_index = np.random.randint(m)
xi = X[random_index:random_index+1]
yi = y[random_index:random_index+1]
# 计算预测值
h = np.dot(xi, theta)
# 计算误差
error = h - yi
loss_.append(np.mean(error**2) / 2)
# 计算梯度
gradient = np.dot(xi.T, error)
# 更新参数
theta = theta - alpha * gradient
return theta, loss_
问题:内层for循环里面 xi 只有一个元素呀,为什么可以拟合?
答:迭代的累积效应:随机梯度下降通过外层的for循环控制迭代轮数(_),在内层循环中,每一轮都会随机选择一个样本计算梯度并更新参数。随着迭代的进行,模型会多次接触到数据集中的不同样本,每次更新都会对参数进行微调。例如,在经过大量的迭代后,模型会逐渐 “学习” 到数据的整体分布特征,就像不断打磨一个雕塑,每次只做一点修改,但最终能塑造出理想的形状。
遍历整个数据集:经过多轮迭代,理论上每个样本都会有机会被选中用于更新参数。这样,模型就能够综合考虑数据集中所有样本的信息,从而对数据进行拟合。
总代码:
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['Microsoft YaHei']
# 定义随机梯度下降函数
def stochastic_gradient_descent(X, y, alpha, num_iter):
m, n = X.shape
theta = np.random.randn(n, 1) # 随机初始化参数
loss_ = [] # 定义一个空列表,进行损失数据的存储
for _ in range(num_iter):
for i in range(m):
# 随机选择一个样本,即只使用一个数据进行拟合,找到最优解
random_index = np.random.randint(m)
xi = X[random_index:random_index+1]
yi = y[random_index:random_index+1]
# 计算预测值
h = np.dot(xi, theta)
# 计算误差
error = h - yi
loss_.append(np.mean(error**2) / 2)
# 计算梯度
gradient = np.dot(xi.T, error)
# 更新参数
theta = theta - alpha * gradient
return theta, loss_
# 生成一些示例数据
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)
# 添加偏置项
X_b = np.c_[np.ones((100, 1)), X]
# 设置超参数
alpha = 0.009 # 这个
num_iterations = 10
# 执行批量梯度下降
theta, loss_ = stochastic_gradient_descent(X_b, y, alpha, num_iterations)
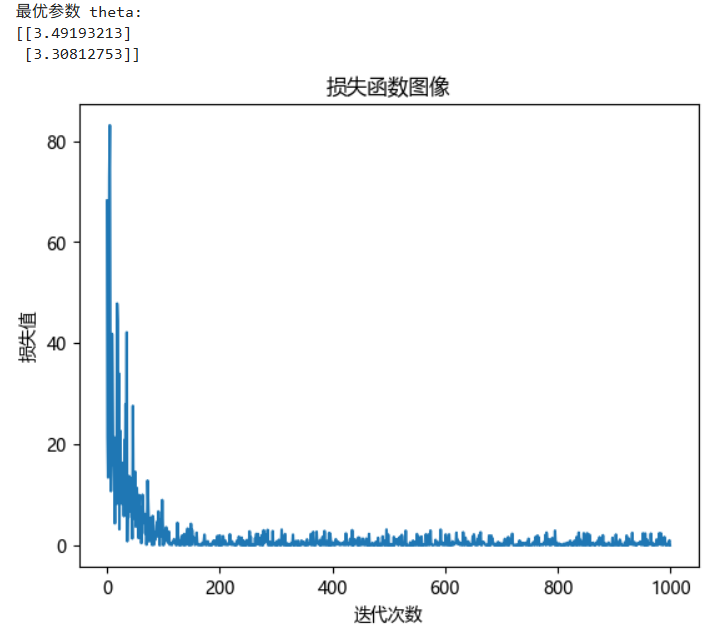
print("最优参数 theta:")
print(theta)
plt.plot(range(len(loss_)), loss_, label="损失函数图像")
plt.title("损失函数图像")
plt.xlabel("迭代次数")
plt.ylabel("损失值")
plt.show()
在合适的学习率下,损失函数在梯度下降法的作用下,损失值会趋于收敛,但是拟合结果的稳定性不是很好,损失值会有微小波动,会产生误差。
3.2.3 优缺点
- 优点:
- 计算效率高:每次迭代只需要处理一个样本,因此在大规模数据集上训练速度比批量梯度下降快得多,内存需求也较低。
- 能够跳出局部最优:由于每次迭代使用的是单个样本的梯度,参数更新具有一定的随机性,这使得算法有可能跳出局部最优解,更有机会找到全局最优解。
- 缺点:
- 梯度更新的方差大:每次只使用一个样本的梯度进行更新,导致梯度估计的方差较大,参数更新过程可能会出现较大的波动,使得收敛过程不稳定。
- 可能无法收敛到精确的全局最优解:由于更新的随机性,最终可能在全局最优解附近震荡,难以精确收敛到全局最优解。
3.3 Mini-batch Gradient Descent
3.3.1 数学原理
小批量梯度下降(Mini - batch Gradient Descent,MBGD)是批量梯度下降(Batch Gradient Descent,BGD)和随机梯度下降(Stochastic Gradient Descent,SGD)的折中方案。批量梯度下降在每次迭代时使用整个训练数据集来计算梯度并更新参数,计算量较大;随机梯度下降每次只使用一个样本进行更新,梯度更新的方差较大,收敛过程不稳定。而小批量梯度下降每次从训练数据集中随机选取一小批量(mini - batch)样本,使用这一小批量样本的梯度来更新参数。
假设我们有m个样本的训练数据集: { ( x ( 1 ) , y ( 1 ) ) , ( x ( 2 ) , y ( 2 ) ) , ⋯ , ( x ( i ) , y ( i ) ) , ⋯ , ( x ( m ) , y ( m ) ) } \{(x^{(1)},y^{(1)}),(x^{(2)},y^{(2)}),\cdots,(x^{(i)},y^{(i)}),\cdots,(x^{(m)},y^{(m)}) \} {(x(1),y(1)),(x(2),y(2)),⋯,(x(i),y(i)),⋯,(x(m),y(m))},我们将数据集划分为若干个小批量,每个小批量包含 b b b个样本( b < m b < m b<m)。设第 t t t个小批量的样本集合为 β t = { ( x ( i ) , y ( i ) ) : i ∈ I t } \beta_{t}=\{(x^{(i)},y^{(i)}):i\in\mathcal{I} _{t}\} βt={(x(i),y(i)):i∈It},其中 I t \mathcal{I}_{t} It是第t个小批量样本的索引集合,且 ∣ I t ∣ = b |\mathcal{I}_{t}|=b ∣It∣=b。
目标是最小化损失函数 J ( θ ) J(\theta) J(θ),即:
J ( θ ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 J(\theta)=\frac{1}{2m}\sum_{i=1}^m(h_{\theta}(x^{(i)})-y^{(i)})^2 J(θ)=2m1∑i=1m(hθ(x(i))−y(i))2
在小批量梯度下降中,每次迭代使用第t个小批量样本计算梯度:
∇ θ J ( θ ) = 1 2 b ∑ i ∈ I t ∇ θ ( h θ ( x ( i ) ) − y ( i ) ) 2 = 1 b X T ( h θ ( X ) − y ) , X ∈ I t 更新参数 θ i + 1 = θ i − α ∇ θ J ( θ ) \begin{array}{l} \nabla_{\theta}J(\theta)&=\frac{1}{2b}\sum_{i\in\mathcal{I} _{t}}\nabla_{\theta}(h_{\theta}(x^{(i)})-y^{(i)})^2 \\ &=\frac{1}{b}X^T(h_{\theta}(X)-y),X\in\mathcal{I} _{t} \\ 更新参数&\theta_{i+1}=\theta_{i}-\alpha \nabla_{\theta}J(\theta) \end{array} ∇θJ(θ)更新参数=2b1∑i∈It∇θ(hθ(x(i))−y(i))2=b1XT(hθ(X)−y),X∈Itθi+1=θi−α∇θJ(θ)
3.3.2 代码实现
函数块:
# 定义小批量梯度下降函数
def mini_batch_gradient_descent(X, y, alpha, num_iter, batch_size):
m, n = X.shape
theta = np.random.randn(n, 1) # 随机初始化参数
num_batches = m // batch_size
loss_ = [] # 存储损失率的变化
for _ in range(num_iter):
# 打乱数据集
shuffled_indices = np.random.permutation(m) # 打乱数组的顺序,也即实现随机性
# 会返回一个包含 0 到 m-1 这 m 个整数的随机排列数组,进而实现打乱
X_shuffled = X[shuffled_indices]
y_shuffled = y[shuffled_indices]
for batch in range(num_batches):
# 选取小批量样本
start_index = batch * batch_size
end_index = start_index + batch_size
xi = X_shuffled[start_index:end_index]
yi = y_shuffled[start_index:end_index]
# 计算预测值
h = np.dot(xi, theta)
# 计算误差
error = h - yi
loss_.append(np.mean(error ** 2) / 2)
# 计算梯度
gradient = (1 / batch_size) * np.dot(xi.T, error)
# 更新参数
theta = theta - alpha * gradient
return theta, loss_
总代码:
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['Microsoft YaHei']
# 定义小批量梯度下降函数
def mini_batch_gradient_descent(X, y, alpha, num_iter, batch_size):
m, n = X.shape
theta = np.random.randn(n, 1) # 随机初始化参数
num_batches = m // batch_size
loss_ = [] # 存储损失率的变化
for _ in range(num_iter):
# 打乱数据集
shuffled_indices = np.random.permutation(m) # 打乱数组的顺序,也即实现随机性
# 会返回一个包含 0 到 m-1 这 m 个整数的随机排列数组,进而实现打乱
X_shuffled = X[shuffled_indices]
y_shuffled = y[shuffled_indices]
for batch in range(num_batches):
# 选取小批量样本
start_index = batch * batch_size
end_index = start_index + batch_size
xi = X_shuffled[start_index:end_index]
yi = y_shuffled[start_index:end_index]
# 计算预测值
h = np.dot(xi, theta)
# 计算误差
error = h - yi
loss_.append(np.mean(error ** 2) / 2)
# 计算梯度
gradient = (1 / batch_size) * np.dot(xi.T, error)
# 更新参数
theta = theta - alpha * gradient
return theta, loss_
# 生成一些示例数据
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)
# 添加偏置项
X_b = np.c_[np.ones((100, 1)), X]
# 设置超参数
alpha = 0.1
num_iterations = 10
batch_size = 10
# 执行批量梯度下降
theta, loss_ = mini_batch_gradient_descent(X_b, y, alpha, num_iterations, batch_size = 10)
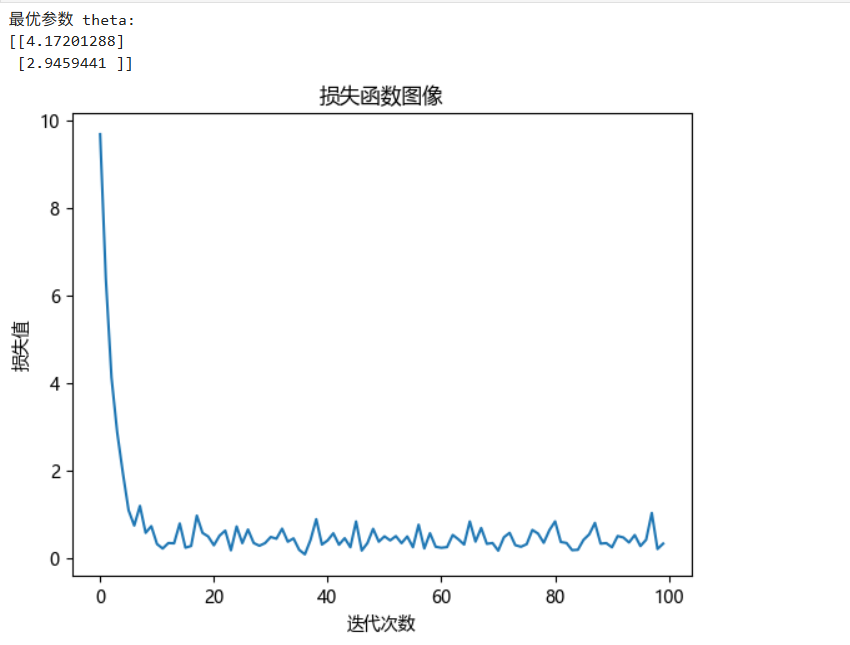
print("最优参数 theta:")
print(theta)
plt.plot(range(len(loss_)), loss_, label="损失函数图像")
plt.title("损失函数图像")
plt.xlabel("迭代次数")
plt.ylabel("损失值")
plt.show()
最终其也有相对于随机梯度下降有更低的损失率的波动性,数据稳定性较强。
3.3.3 优缺点
- 优点:
- 计算效率较高:相比于批量梯度下降,每次只处理一小部分样本,减少了计算量,尤其是在大规模数据集上,训练速度更快。
- 梯度更新较稳定:与随机梯度下降相比,小批量梯度下降使用多个样本的梯度平均,降低了梯度估计的方差,使得参数更新过程更加稳定,收敛速度可能更快。
- 可以利用向量化计算:小批量样本可以通过向量化操作进行处理,充分利用现代计算机的并行计算能力,提高计算效率。
- 缺点:
- 需要选择合适的批量大小:批量大小 b b b 是一个超参数,需要通过实验进行调优。如果批量大小选择不当,可能会影响模型的收敛速度和性能。
- 仍然可能陷入局部最优:虽然比随机梯度下降更稳定,但小批量梯度下降仍然有可能陷入局部最优解。