逻辑回归通常用于解决分类问题。

“分类”是应用逻辑回归的目的和结果，但中间过程依旧是“回归”。通过逻辑回归模型得到连续值，加上一个“阈值”，就成了分类。

逻辑回归算法的拟合函数，叫做Sigmond函数(即形似S的函数。对率函数是Sigmoid的重要代表函数)：
$$y=\frac{1}{1+e^{-z}}$$
多元线性回归方程的一般形式如下：
$$y={\beta }_0+{\beta }_1{x}_1+...+{\beta }_p{x}_p$$
其矩阵形式为：
$$\vec{Y}=\vec{X}\vec{\beta }$$
其中：
$$\vec{Y}=\left[\begin{array}{c}{y}_1\\ y_2\\ ...\\ y_n\end{array}\right],\vec{X}=\left[\begin{array}{c}1x_{11}...x_{1p}\\ ...\\ 1x_{n1}...x_{np}\end{array}\right],\vec{\beta }=\left[\begin{array}{c}{\beta }_0\\ {\beta }_1\\ ...\\ {\beta }_p\end{array}\right]$$
使用Sigmoid函数，将$x$值转换为一个接近0或1的$y$值：
$$y=\frac{1}{1+e^{-(w^{T}x+b)}}$$
可以转为：
$$ln\frac{y}{1-y}=w^{T}x+b$$
其中，$\frac{y}{1-y}$是“几率”，反应了$x$作为正例的相对可能性。

若将$y$视为类后验概率估计$p(y=1|x)$，则为：
$$ln\frac{p(y=1|x)}{p(y=0|x)}=w^{T}x+b$$

$$p(y=1|x)+p(y=0|x)=1$$

所以可以得到：
$$p(y=1|x)=\frac{e^{w^{T}x+b}}{1+e^{w^{T}x+b}}$$

$$p(y=0|x)=\frac{1}{1+e^{w^{T}x+b}}$$

因此可以采用“最大似然法”求解$\vec{w}$，$b$。

似然性(Likelihood) 是一个事件实际已经发生，反推在什么参数条件下，这个事件发生的概率最大。

采用“对数似然”：
$$L(w,b)=\sum _{i=1}^{m}lnp(y_i|x_i;w,b)$$

采用梯度下降进行求解。

原理：通过计算损失函数关于模型参数的梯度，然后沿着梯度的反方向（即最陡峭的下降方向）更新参数。这样，每次迭代都会使损失函数值减小（至少在局部上是这样的），从而逐渐接近损失函数的最小值。

步骤：

Step 1） 初始化参数：选择一个初始的模型参数向量。

Step 2） 计算损失函数对参数的梯度，表示损失函数在当前参数值处的变化率。

Step 3） 沿着梯度的反方向，以一定的学习率更新参数的值，使得损失函数逐渐减小。

Step 4） 重复步骤2和步骤3，直到满足终止条件。

代码实现

数据集下载：Iris - UCI Machine Learning Repository

Iris数据集是有三个目标特征，在这里仅用逻辑回归进行二分类处理，因此删除了后面50个其他目标特征的，使这个数据集符合二分类。

数据集处理：处理出$X$，$Y$，并将$Y$的目标特征非0/1进行转换，在将$Y$设置为$(n,1)$的矩阵形状：

import numpy as np
import pandas as pd

def data_processing():
    data_csv = pd.read_csv('iris.data')
    data_csv = data_csv.dropna()
    # print(data_csv)
    X = data_csv.iloc[:-1, 0:4].values
    # print(X)
    Y = data_csv.iloc[:-1, 4].map({'Iris-setosa': 0, 'Iris-versicolor': 1}).values
    Y = Y.reshape(-1, 1)
    # print(Y.shape)
    return X, Y
data_processing()

逻辑回归模型训练：

import numpy as np
import matplotlib.pyplot as plt

def sigmoid(x: np.array):
    return 1 / (1 + np.exp(-x))


def trains(X: np.array, Y: np.array, theta: np.array, learn_rate: float, epochs: int):
    """
    定义trains函数，用于训练逻辑回归模型
    X: np.array，特征矩阵，形状为(m, n)，其中m是样本数量，n是特征数量
    Y: np.array，目标变量，形状为(m, 1)，表示每个样本的标签（0或1）
    theta: np.array，模型参数，形状为(n, 1)，表示每个特征的权重
    learn_rate: float，学习率，控制参数更新的步长
    epochs: int，迭代次数，表示训练模型的轮数
    """
    m = len(Y)
    
    loss_values = np.zeros((epochs, 1))
    # 进行多次迭代训练
    for epoch in range(epochs):
        z = X @ theta
        # 计算预测值h，通过sigmoid函数将z映射到(0, 1)之间
        h = sigmoid(z)
        # 计算损失loss，即预测值h与实际值Y之间的差异
        loss = h - Y
        # 计算梯度gradient，根据损失和特征矩阵计算参数的梯度
        gradient = X.T @ loss / m
        # 更新参数theta，使用梯度下降法，学习率乘以梯度
        theta -= learn_rate * gradient
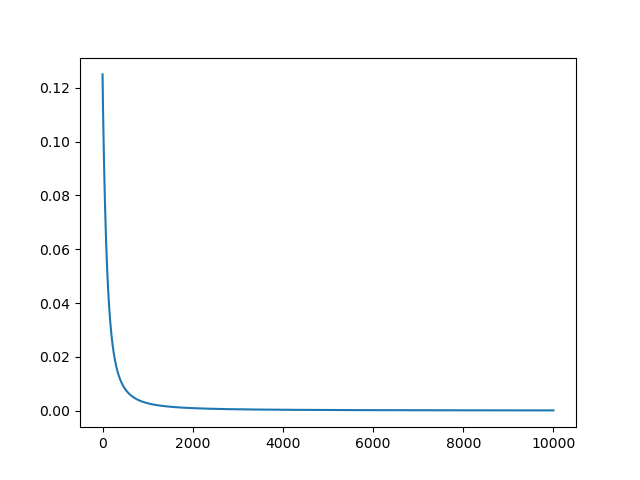
        loss_values[epoch] = np.sum(loss ** 2) / (2 * m)
    
    plt.plot(loss_values)
    plt.show()
    # 返回训练后的参数theta
    return theta

import data_processing as dp

X, Y = dp.data_processing()
print(trains(X, Y, np.zeros((X.shape[1], 1)), 0.01, 10000))

用人话讲明白逻辑回归Logistic regression - 知乎 (zhihu.com)

Python实现逻辑回归(Logistic Regression)_python 逻辑回归-CSDN博客