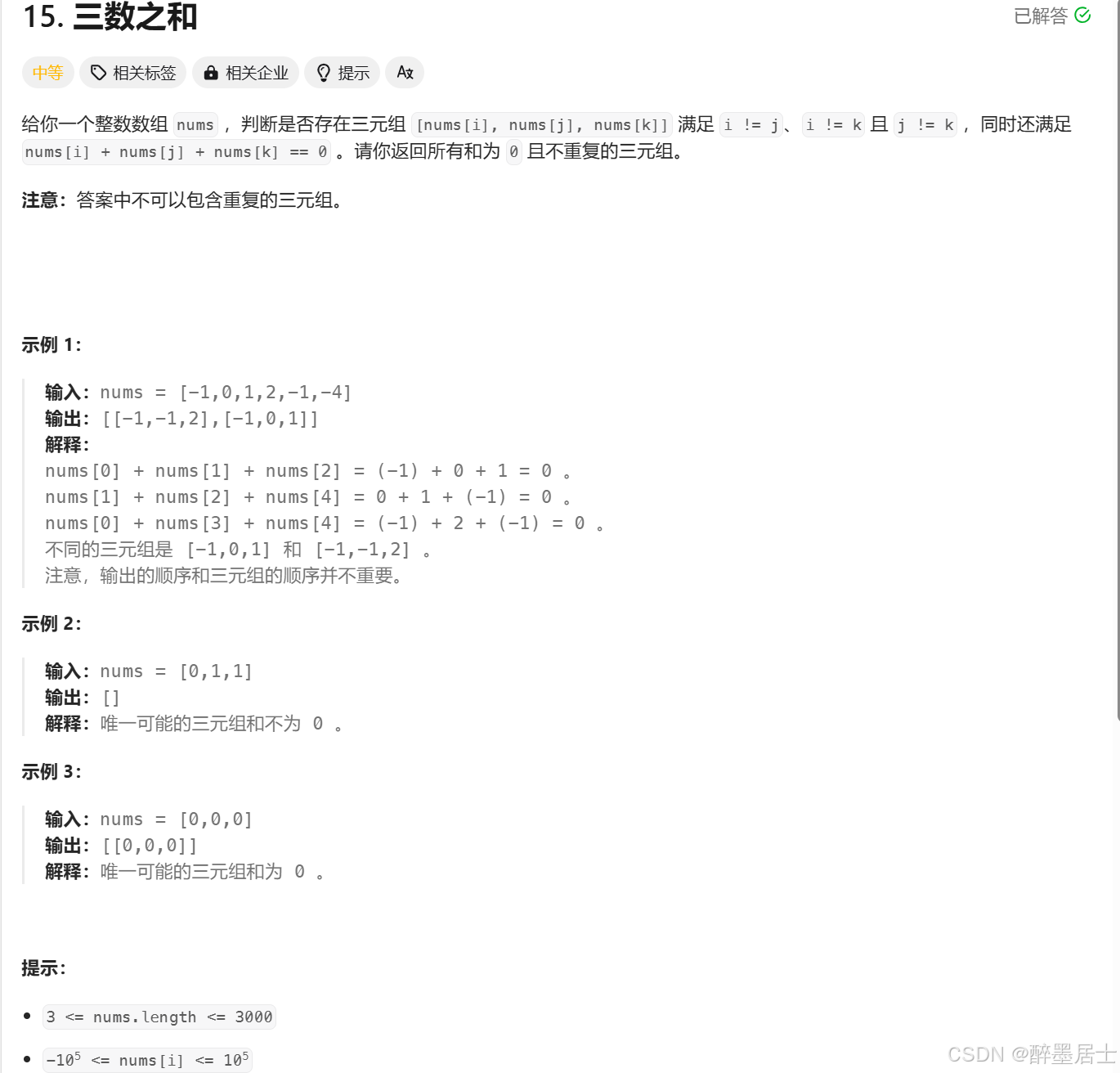
题目描述
题解思路
这道题如果我们直接使用三层循环暴力搜索,时间复杂度是O(n3),大概率会超时
那还有更优解吗,答案是绝对的,查询搜索想要优化,就要思考如何进行排除法加速搜索过程。我们可以使用哈希表存储数组中所有的数字,然后我们只需要两层循环遍历哈希表,枚举所有的两个数字的组合,通过 0 - 两个数字之和得到另一个数字的大小,然后在哈希表中查看是否存在,若存在,则表明找到一个三元组,通过这种做法要注意最终得到的所有三元组需要去重,这个过程的时间复杂度是O(n2),空间复杂度是O(n)。
我们还能找到其它解法吗,答案是绝对的,我们可以先对数组进行排序,然后遍历数组,先固定三元组中的最小值,然后在剩余区间内使用相撞的双指针,如果找到的三数之和小于0右移左指针,若大于0则左移右指针,若过程中存在三数之和等于0的情况,则记录该三元组并结束对撞过程,这种做法注意需要对我们遍历到的最小值、左指针、右指针进行去重,避免产生重复的结果,该算法时间复杂度是O(n2),空间复杂度是使用的排序算法的空间复杂度
题解代码
func threeSum(nums []int) [][]int {
// 数组排序
sort.Ints(nums)
// 结果集合
ans := make([][]int, 0)
for i := 0; i < len(nums) - 2; i++ {
// 如果最小值小于零,则不可能在出现组成三元组的情况,进行剪枝
if nums[i] > 0 {
break
}
// 进行相撞的左右指针
left, right := i + 1, len(nums) - 1
// 如果左右指针未碰撞,进行相撞
for left < right {
// 三数之和
sum := nums[i] + nums[left] + nums[right]
if sum > 0 {
// 小于0,表示三数之和大了,左移右指针
right--
} else if sum < 0 {
// 小于0,表示三数之和小了,右移左指针
left++
} else {
// 记录三元组
ans = append(ans, []int{nums[i], nums[left], nums[right]})
// 找寻下一个不重复的左指针,否则直至越界
for left + 1 <= right && nums[left] == nums[left + 1] {
left++
}
left++
// 找寻下一个不重复的右指针,否则直至越界
for right - 1 >= left && nums[right] == nums[right - 1] {
right--
}
right--
}
}
// 找寻下一个不重复的最小值,否则直至越界
for i + 1 <= right && nums[i] == nums[i + 1] {
i++
}
}
return ans
}