目录

1、代码框架✨

①确认递归函数，参数🧩

②确认终止条件🧩

③处理目前搜索节点出发的路径🧩

2、图的存储✨

 2.1 邻接矩阵✍

2.2 邻接表✍

3、经典例题✨

3.1 所有可达路径 ---模版题

​邻接矩阵存储

邻接表存储 

3.2 岛屿数量 

3.3 岛屿的最大面积 

3.4 n-皇后问题 

4、dfs应用场景 ✨

5、补充知识✨

5.1 参数的传递方式 

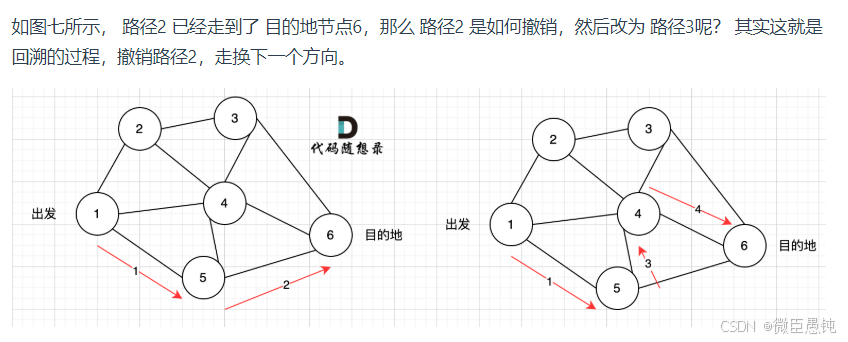
        没有理论基础的先看 深度优先搜索理论基础 | 代码随想录 卡哥讲解的，很通俗易懂~，简单概括“📌深度优先搜索（Depth First Search，简称 DFS）是一种在图或树等数据结构中遍历节点的算法。它沿着一个方向不断深入，直到无法继续为止，然后回溯并探索其他路径。”本篇主要介绍dfs的代码实现，并枚举总结了几道经典例题。

         之前我跟着yxc大佬学习的dfs 也发表总结了相关博客 ，（ps:总感觉存储结构很复杂，到现在再看已经看不懂了哈哈哈）ACWing【846】树的重心、图中点的层次 、邻接表存储图/树、dfs/bfs搜索图/树_图中点的层次acwing-CSDN博客

1、代码框架✨

        dfs搜索可一个方向，并需要回溯，所以用递归的方式来实现 【真的和回溯的模版很像，没有接触过回溯的可以先看看 代码随想录 对回溯算法 的介绍】

        代码框架：

vector<vector<int>> result; // 存放所有符合条件的路径
vector<int> path;           // 存放当前遍历路径

void dfs(参数) {
    if (终止条件) {
        result.push_back(path); // 保存结果
        return;
    }
    for (选择：当前节点的邻居节点) {
        path.push_back(选择);   // 处理节点
        dfs(图，选择的结点);              // 递归
        path.pop_back();        // 回溯
    }
}

深搜三部曲，解读 dfs的代码框架

①确认递归函数，参数🧩

void dfs(参数)

        深搜需要 二维数组数组结构保存所有路径，需要一维数组保存单一路径，这种保存结果的数组，我们可以定义一个全局变量，避免让我们的函数参数过多。 

vector<vector<int>> result; // 保存符合条件的所有路径
vector<int> path; // 起点到终点的路径
void dfs (图，目前搜索的节点) 

②确认终止条件🧩

if (终止条件) {
    存放结果;
    return;
}

 终止添加不仅是结束本层递归，同时也是我们收获结果的时候。

③处理目前搜索节点出发的路径🧩

一般这里就是一个for循环的操作，去遍历 目前搜索节点 所能到的所有节点。

for (选择：本节点所连接的其他节点) {
    处理节点;
    dfs(图，选择的节点); // 递归
    回溯，撤销处理结果
}

 举例：

2、图的存储✨

还是哦我们只介绍如何用代码实现，理论知识可以看 图论理论基础 | 代码随想录 知道这两种存储方式的优缺点，分别适合什么场景

 2.1 邻接矩阵✍

        邻接矩阵 使用 二维数组来表示图结构。 邻接矩阵是从节点的角度来表示图，有多少节点就申请多大的二维数组。

        如果有n 个节点，节点标号是从1开始的，为了节点标号和下标对齐，所以我们需要申请 n + 1 * n + 1 这么大的二维数组。【掌握用vector定义二维数组】

vector<vector<int>> graph(n + 1, vector<int>(n + 1, 0));

        输入m个边，构造方式如下： 

while (m--) {
    cin >> s >> t;
    // 使用邻接矩阵 ，1 表示 节点s 指向 节点t
    graph[s][t] = 1;
}

2.2 邻接表✍

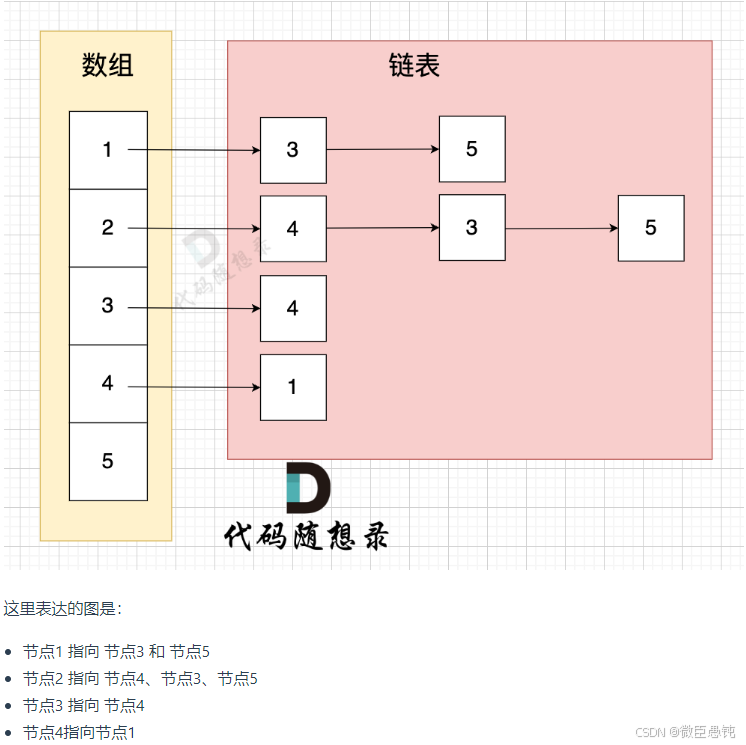
        邻接表 使用 数组 + 链表的方式来表示。 邻接表是从边的数量来表示图，有多少边 才会申请对应大小的链表。

需要构造一个数组，数组里的元素是一个链表【list 是 STL中的一个双向链表容器】

// 节点编号从1到n，所以申请 n+1 这么大的数组
vector<list<int>> graph(n + 1); // 邻接表，list为C++里的链表

 输入m个边，构造方式如下：

while (m--) {
    cin >> s >> t;
    // 使用邻接表 ，表示 s -> t 是相连的
    graph[s].push_back(t);
}

3、经典例题✨

3.1 所有可达路径 ---模版题

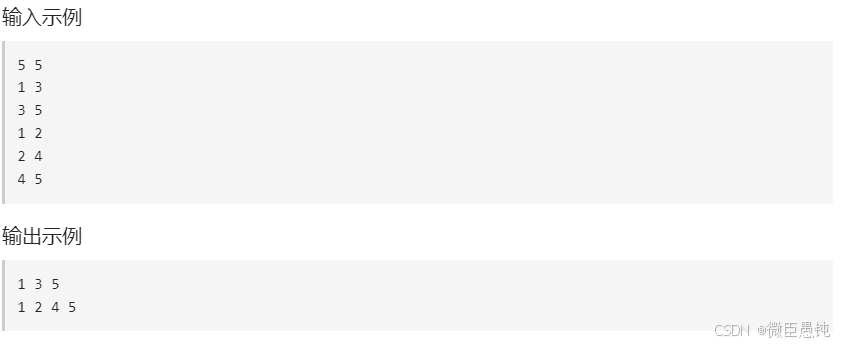
 邻接矩阵存储

#include <bits/stdc++.h> 
using namespace std;

vector<int> path;               // 当前路径，用于记录 DFS 遍历过程中的节点
int n, m;                       // n 表示节点数，m 表示边数
vector<vector<int>> res;        // 存储所有从起点到终点的路径

// 深度优先搜索函数
// graph：图的邻接矩阵表示
// x：当前访问的节点
// n：目标节点
void dfs(const vector<vector<int>>& graph, int x, int n) {
    // 如果当前节点是目标节点，说明找到一条完整路径
    if (x == n) {
        res.push_back(path);    // 将当前路径存入结果集
        return;
    }

    // 遍历所有节点，寻找与当前节点相连的下一个节点
    for (int i = 1; i <= n; i++) {
        if (graph[x][i] == 1) {  // 如果存在从 x 到 i 的边
            path.push_back(i);   // 将节点 i 加入路径
            dfs(graph, i, n);    // 递归访问节点 i
            path.pop_back();     // 回溯：移除最后访问的节点，尝试其他路径
        }
    }
}

int main() {
    // 输入节点数 n 和边数 m
    cin >> n >> m;

    // 使用邻接矩阵表示图，初始值为 0（表示无边）
    vector<vector<int>> graph(n + 1, vector<int>(n + 1, 0));

    // 输入每条边的信息
    while (m--) {
        int s, t;
        cin >> s >> t;
        graph[s][t] = 1;  // 标记从 s 到 t 有一条有向边
    }

    path.push_back(1);       // 从起点 1 开始遍历
    dfs(graph, 1, n);        // 调用 DFS 查找所有从 1 到 n 的路径

    // 如果没有找到任何路径，输出 -1
    if (res.size() == 0) 
        cout << "-1" << endl;
    else {
        // 输出所有找到的路径
        for (auto it : res) {
            for (int i = 0; i < it.size() - 1; i++) {
                cout << it[i] << " ";  // 输出路径中的节点+一个空格（除最后一个外）
            }
            cout << it[it.size() - 1] << endl;  // 输出路径的最后一个节点并换行，没有空格
        }
    }

    return 0;
}

邻接表存储 

#include <bits/stdc++.h>
using namespace std;

// 全局变量：
// n: 图中节点的数量
// m: 图中边的数量
// res: 存储所有路径的结果
// path: 存储当前路径
int n, m;
vector<vector<int>> res;  // 用于存放所有从1到n的路径
vector<int> path;  // 用于记录当前的路径

// 深度优先搜索（DFS）函数
// 参数 graph: 邻接表表示的图，x: 当前节点，n: 目标节点
void dfs(const vector<list<int>>& graph, int x, int n) {
    // 如果当前节点是目标节点 n
    if (x == n) {
        // 找到一条从1到n的路径，将其添加到结果中
        res.push_back(path);
        return;
    }
    // 遍历当前节点 x 的所有邻接节点
    for (auto it : graph[x]) {
        // 将邻接节点 it 加入当前路径
        path.push_back(it);
        // 递归访问邻接节点
        dfs(graph, it, n);
        // 递归返回后，弹出当前节点，回溯
        path.pop_back();
    }
}

int main() {
    // 输入图的节点数和边数
    cin >> n >> m;
    // 初始化邻接表，大小为 n+1，因为节点编号从 1 开始
    vector<list<int>> graph(n + 1); 
    
    // 输入图的每条边，并构建邻接表
    while (m--) {
        int s, t;
        cin >> s >> t;
        graph[s].push_back(t);  // 从 s 到 t 存在一条边
    }
    
    // 从节点 1 开始，初始化路径
    path.push_back(1); 
    
    // 调用 DFS 寻找从节点 1 到节点 n 的所有路径
    dfs(graph, 1, n);

    // 如果没有找到路径
    if (res.size() == 0) {
        cout << "-1" << endl;  // 输出 -1 表示没有路径
    } else {
        // 输出所有找到的路径
        for (auto it : res) {
            for (int i = 0; i < it.size() - 1; i++) {
                cout << it[i] << " ";  // 输出路径中的每个节点
            }
            // 输出路径的最后一个节点，不加空格
            cout << it[it.size() - 1] << endl;
        }
    }
    return 0;
}

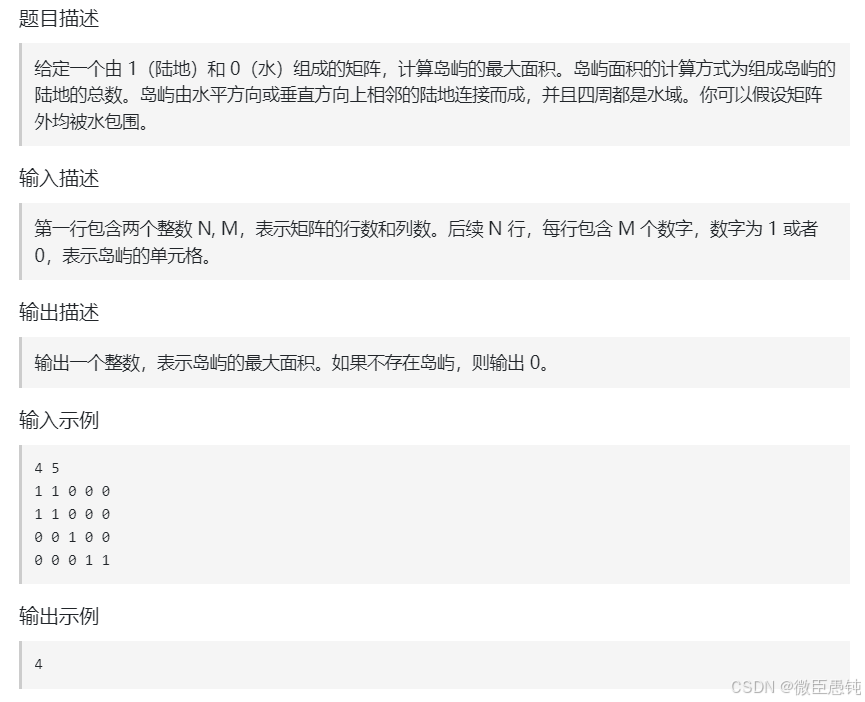
3.2 岛屿数量 

解题思路 ：

 代码：

#include<bits/stdc++.h>
using namespace std;

// 定义网格的大小
int n, m;  
// 四个方向：右、下、左、上
int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1}; 

// 用于记录岛屿的数量
int result = 0;

// 深度优先搜索（DFS）函数：用于标记与当前陆地相连的所有陆地
void dfs(const vector<vector<int>>& graph, vector<vector<int>>& visited, int x, int y) {
    // 终止条件：如果当前位置已经访问过或者是水域（0），就返回
    if (visited[x][y] || graph[x][y] == 0) return;
    
    // 将当前格子标记为已访问
    visited[x][y] = 1;

    // 遍历四个方向（上下左右）
    for (int i = 0; i < 4; i++) {
        // 计算下一个位置的坐标
        int nex = x + dir[i][0];
        int ney = y + dir[i][1];

        // 如果下一个位置超出网格范围，就跳过
        if (nex >= n || nex < 0 || ney >= m || ney < 0) continue;

        // 递归调用DFS，访问相邻的陆地
        dfs(graph, visited, nex, ney);
    }
}

int main() {
    // 输入网格的行数和列数
    cin >> n >> m;

    // 创建一个n行m列的网格，初始化为0（水域）
    vector<vector<int>> graph(n, vector<int>(m, 0));

    // 输入网格的每个元素，1代表陆地，0代表水域
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            cin >> graph[i][j];
        }
    }

    // 创建一个n行m列的访问标记数组，初始化为0（未访问）
    vector<vector<int>> visited(n, vector<int>(m, 0));

    // 遍历整个网格
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            // 如果当前格子是陆地且未访问过
            if (!visited[i][j] && graph[i][j] == 1) {
                // 发现一个新的岛屿，岛屿数加1
                result++;
                // 使用DFS标记当前岛屿的所有陆地为已访问
                dfs(graph, visited, i, j);
            }
        }
    }

    // 输出岛屿的总数
    cout << result << endl;
    return 0;
}

3.3 岛屿的最大面积 

代码直接在岛屿数量这道题目上添加面积的存储即可。

#include <bits/stdc++.h>
using namespace std;

int n, m;  // 网格的行数和列数
int dir[4][2] = {0, 1, 1, 0, 0, -1, -1, 0};  // 四个方向：右、下、左、上
int result = 0;  // 用于记录岛屿的最大面积

// 深度优先搜索（DFS）函数：用于计算与当前陆地相连的所有陆地的面积
int dfs(const vector<vector<int>>& graph, vector<vector<int>>& visited, int x, int y) {
    // 终止条件：如果当前位置超出边界、已经访问过或者是水域（0），就返回面积为0
    if (x < 0 || x >= n || y < 0 || y >= m || visited[x][y] || graph[x][y] == 0) {
        return 0;
    }

    // 将当前格子标记为已访问
    visited[x][y] = 1;

    // 当前岛屿面积初始化为1（当前格子）
    int area = 1;

    // 遍历四个方向（上下左右）
    for (int i = 0; i < 4; i++) {
        int nx = x + dir[i][0];
        int ny = y + dir[i][1];
        // 递归调用DFS，访问相邻的陆地，并累加面积
        area += dfs(graph, visited, nx, ny);
    }

    return area;  // 返回当前岛屿的面积
}

int main() {
    // 输入网格的行数和列数
    cin >> n >> m;

    // 创建一个n行m列的网格，初始化为0（水域）
    vector<vector<int>> graph(n, vector<int>(m));
    // 创建一个n行m列的访问标记数组，初始化为0（未访问）
    vector<vector<int>> visited(n, vector<int>(m));

    // 输入网格的每个元素，1代表陆地，0代表水域
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            cin >> graph[i][j];
        }
    }

    // 遍历整个网格
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            // 如果当前格子是陆地且未访问过
            if (!visited[i][j] && graph[i][j] == 1) {
                // 使用DFS计算当前岛屿的面积，并更新最大面积
                result = max(result, dfs(graph, visited, i, j));
            }
        }
    }

    // 输出岛屿的最大面积
    cout << result << endl;
    return 0;
}

3.4 n-皇后问题 

ACWing【843】n皇后问题_acwing n皇后问题-CSDN博客  之前在acwing上做过一遍

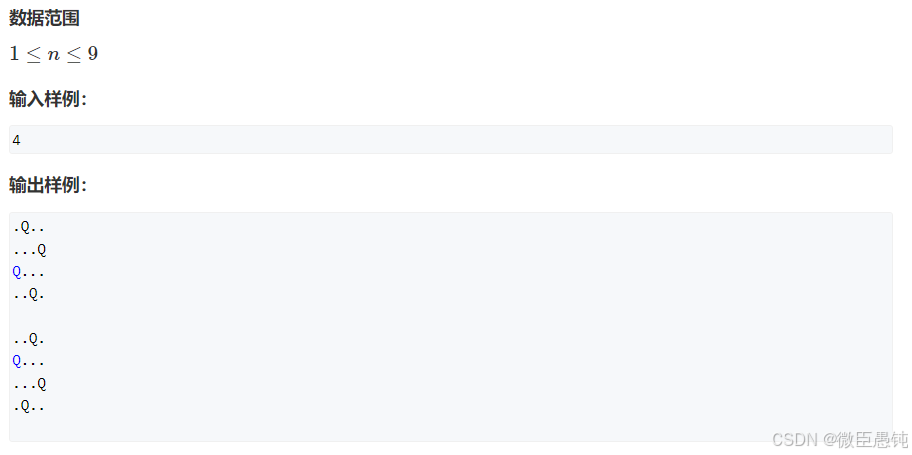
#include <bits/stdc++.h>
using namespace std;

const int N = 20; // 定义最大行列数
vector<vector<int>> result; // 存放所有符合条件的路径
vector<int> path;           // 存放当前遍历路径
int n;                       // 棋盘大小
bool row[N], dg[N], udg[N];  // 标记列、对角线和反对角线是否被占用

// 深度优先搜索（DFS）函数
void dfs(int u) {
    if (u == n) { // 如果已经放置了 n 个皇后，找到一组解
        result.push_back(path); // 将当前路径保存到结果中
        return;
    }

    // 枚举当前行 u 的每一列 y
    for (int y = 0; y < n; y++) {
        // 检查当前列 y 和对角线是否被占用
        if (!row[y] && !dg[y - u + n] && !udg[y + u]) {
            path.push_back(y); // 将当前列 y 加入路径
            row[y] = dg[y - u + n] = udg[y + u] = true; // 标记当前列和对角线为占用
            dfs(u + 1); // 递归放置下一个皇后
            path.pop_back(); // 回溯，移除当前列 y
            row[y] = dg[y - u + n] = udg[y + u] = false; // 恢复当前列和对角线的状态
        }
    }
}

int main() {
    cin >> n; // 输入棋盘大小
    dfs(0);   // 从第 0 行开始递归放置皇后

    // 输出所有结果
    for (const auto& res : result) {
        for (int y : res) {
            for (int i = 0; i < n; i++) {
                if (i == y) {
                    cout << "Q "; // 如果当前列是皇后所在位置，输出 Q
                } else {
                    cout << ". "; // 否则输出 .
                }
            }
            cout << endl;
        }
        cout << endl; // 每组解之间输出一个空行
    }

    return 0;
}

4、dfs应用场景 ✨

• 图的遍历

  • 拓扑排序（有向无环图

  • 遍历无向图或有向图的所有节点。

  • 检测图中是否存在环。

  • 求解图的连通分量（无向图）或强连通分量（有向图）。

• 路径搜索

  • ​​​​​寻找从起点到终点的所有路径（如上述代码中的从节点1到节点n的所有路径）。

  • 寻找最短路径（结合剪枝或记忆化搜索）。

  • 寻找最长路径或满足特定条件的路径

• 树的遍历

  • ​​​​​​​​​​​​​​遍历二叉树或N叉树。

  • 计算树的高度、深度或宽度。

  • 求解树的直径（最长路径）

• 组合与排列问题

  • ​​​​​​​​​​​​​​生成所有可能的排列（如全排列问题）。

  • 生成所有可能的组合（如组合总和问题）。

  • 生成所有子集（如子集问题）

• 搜索与回溯

  • ​​​​​​​​​​求解背包问题（结合动态规划）

  • 解决数独问题。

  • 求解八皇后问题。

  • 求解迷宫问题。

5、补充知识✨

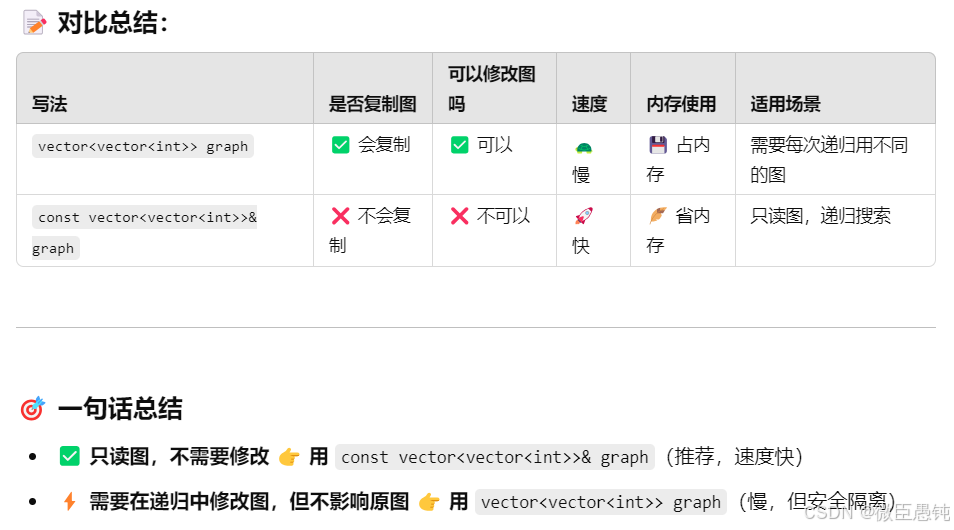
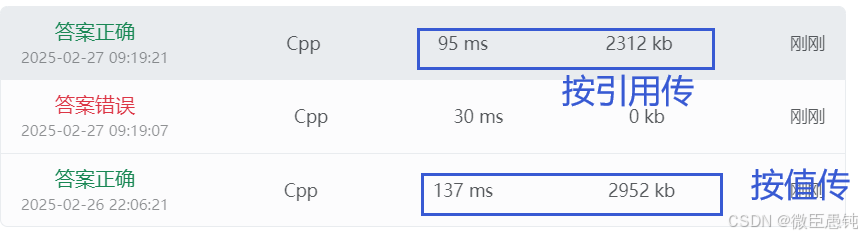
5.1 参数的传递方式 

对于 所有可达路径这道题 ：

•   const关键字用于声明变量或参数为“只读”，表示该变量或参数的值在声明后不能被修改。当函数不需要修改传入的参数时，可以将参数声明为const
•   & 用于声明引用类型，表示该变量是另一个变量的别名。引用在函数参数传递中非常有用，可以避免复制数据。如visited参数

               

•   const &：结合使用时，表示一个只读引用，既保护了数据，又避免了复制，常用于函数参数传递。如dfs中作为原始图的参数graph。