决策树

理论部分：

一、分类树

决策树是一种用于分类和回归的预测模型，它通过树状结构来表示决策过程。

决策树的优缺点：

• 优点：易于理解和解释，能够处理非线性数据，并且不需要假设数据分布。
• 缺点：容易过拟合和对噪声数据敏感，通过适当的剪枝和交叉验证，可以减少这些问题。

假设数据的所有特征都是二元特征（或二值特征），在创建决策树的时候，我们需要选择一个合适的特征，将数据进行分为两个最佳的部分，如何选择这个合适的特征？

要想选择一个合适的特征，我们需要有一个标准来供我们进行比较。

1. 数据纯度的定义 — — 熵：

$P_1$：表一种类别的数据占总数居的比例。

$P_0=1-P_1$：表示除了$P_1$类别以外的其他数据占总数据的比例。

熵函数：$H(P_1)=-P_1\log P_1-P_0\log P_0=-P_0\log P_1-(1-P_1)\log (1-P_1)$

2. 信息增益（ID3）

在决策树中，熵的减少称为信息增益，信息增益越大，熵的值越小，数据的混乱程度越小。

定义：

• $P_1^{left}$：表示分类后左子节点中，正样例占左字节点的比例。
• $W^{left}$：表示分类后左子节点所有样本占分类前所有样本的比例。
• $P_1^{right}$：表示分类后右子节点中，正样例占右字节点的比例。
• $W^{right}$：表示分类后右子节点所有样本占分类前所有样本的比例。

信息增益（Information Gain）：= $H(P_1^{root})-(W^{left}H(P_1^{left}+w^{right}H(P_1^{right})))$

3. 其它决策依据

用信息增益来选取特征划分的方法，不适用于存在一个特征的可选值很多的情况。

信息增益率（C4.5）

信息增益率（Information Gain Ratio）是决策树算法中用于选择特征的一种方法，特别是在C4.5算法中。它在信息增益的基础上进一步考虑了特征的分裂能力，以避免选择那些具有许多值的特征，因为这些特征可能会产生许多分支，从而导致过拟合。
$$信息增益率=\frac{信息增益}{该特征的熵值}$$

基尼系数（CART）

基尼系数是一种衡量数据不纯度的指标。在决策树的上下文中，不纯度是指数据集中不同类别（对于分类问题）或不同数值（对于回归问题）的混合程度。基尼系数的值介于0到1之间，值越小表示数据越纯：

• 0：数据完全纯净，即所有样本属于同一类别或具有相同的数值。
• 1：数据完全混合，每个类别或数值的分布都是均匀的。

$$Gini(p)=1-\sum _{i=1}^n{p}_i^2$$

其中，$p_i$是类别$i$在数据集中的比例。

对于给定的特征A，将其应用于数据集D，得到若干子集 $D_1,D_2,D_3,\cdots ,D_T$，然后计算分裂后的基尼系数：
$$\text{Gini}(D)=\sum _{i=1}^{|T|}\left(\frac{|D_i|}{|D|}\cdot \text{Gini}(D_i)\right)$$

其中，$D_i$是特征A的第$i$个子集，$T$ 是数据集中分类的类别个数，$D_i$是属于类别$i$的数据子集，$|D_i|$是子集$D_i$中的样本数量，$|D|$ 是原始数据集D中的总样本量。

选择最佳特征：

选择使得基尼系数降低最大的特征作为分裂节点的特征，这个降低的量称为基尼增益：

$$\text{Gini Gain(D, A) = Gini(D) - Gini(D, A)}$$

4. 分类树的构建过程

1. 从根节点处的所有训练示例开始，计算所有可能特征的信息增益，并据此选择要拆分的特征，从而提供最高的信息增益。
2. 依据所选特征，将数据拆分为两个子集，创建树的左右分支，将训练示例发送到左侧或右侧的分支。
3. 继续在树的左分支和右分支上重复拆分过程，直到满足终止条件。

5. 终止条件：

1. 当一个节点100%是单一类型的数据，熵已经达到零。
2. 当进一步拆分节点将导致树超过您设置的最大深度。
3. 节点中的示例数量低于设定的阈值。
4. 分割的信息增益小于设定的阈值。

6. One-hot（独热编码）

对于决策树，如果特征不再是二元特征，而是一个特征对应更多可能的值，应该如何进行编码？（二元特征可以使用0，1编码）

我们可以使用One-hot来进行编码，如果一个分类特征可以取$K$个可能的值，那么我们将通过创建$K$个只能取0或1的二进制特征来替换它。

如有三个特征：可以用（1，0，0），（0，1，0），（0，0，1）这三个编码来进行分类。

二、回归树

1. 基本概念

1. 目标变量：对于回归树，目标变量是一个连续的数值，比如房价、温度或者任何其他可以被量化的度量。
2. 预测：回归树的目的是预测这些连续值，与分类树不同，后者预测的是类别标签。
3. 训练数据：回归树的训练数据包含特征和目标变量的观测值

一个简单的例子：通过动物的一系列特征来预测动物的体重（体重是指体重的平均值，因为分类最后的叶子节点得到的是一个方差很小的不同的值的集合，我们取这些值的平均值表示该叶子节点所代表的值）。

2. 特征选取依据

依据方差减少的情况进行选取，在回归树中我们使用方差来代替信息熵。

3. 例子：

在分类之前体重的方差为20.51，经过某一特征（如：耳朵特征）分类后，得到左边的方差为1.47，右边的方差为21.87，并且$w^{left}=0.5$，$w^{right}=0.5$ 计算类似的信息增益：$H= 20.51 - (0.5 \times 1.47 + 0.5 \times 21.87) $ （这里通过方差表示信息增益中的信息熵），并通过计算其他特征的分类后的信息增益，选取信息增益最大的一个特征进行划分。

三、随机森林

1. 描述

如果将训练集中的数据换了一个或几个，将会导致拆分的最高信息增益特征变为了其他特征。对此，我们可以构建多个决策树，依次对示例进行预测，然后使用投票机制，选取投票更高那个作为预测的结果，这样做会提高决策树的健壮性。

有放回抽样：有放回抽样可以让你构建多个不同的训练集，它与你原来的训练示例有点相似，但也有很大的不同。

2. 详细流程

对已有的数据样本（设有$n$个）进行随机放回抽样，得到$k$个样本的数据集，利用该数据集进行训练一个决策树，并再次随机放回抽样得到$k$个样本数据集，训练第二个决策树，继续重复，直至训练$B$个决策树，这$B$个决策树组成了随机森林（$B$不大于100），如果数据样本特别大，通常的做法是令$k=\sqrt{n}$

随机森林更稳健的原因是：替换过程导致算法能够发现数据的许多微小变化，并且训练了多个不同的决策树，同时对所有的决策树进行平均变化。

四、XGBoost

XGBoost（eXtreme Gradient Boosting）是一种高效的机器学习算法，它是一种梯度提升框架，使用树算法作为基学习器。XGBoost在许多机器学习竞赛中表现优异，因为它速度快、性能好、可扩展性强。

1. 安装XGBoost

首先，你需要安装XGBoost库。可以通过Python的包管理工具pip来安装：

pip install xgboost

2. 准备数据

将你的数据集分为特征矩阵X和目标向量y。XGBoost支持NumPy数组、Pandas的DataFrame以及Scikit-learn的DenseMatrix和SparseMatrix。

3. 转换数据格式

XGBoost需要DMatrix格式的数据，这可以通过xgboost.DMatrix函数来转换：

import xgboost as xgb

# 假设X是特征矩阵，y是目标向量
dtrain = xgb.DMatrix(X_train, label=y_train)
dtest = xgb.DMatrix(X_test, label=y_test)

4. 设置参数

XGBoost提供了许多参数来调整模型的性能。一些重要的参数包括：

• max_depth：树的最大深度。
• learning_rate或eta：学习率，较小的学习率通常需要更多的迭代次数。
• n_estimators：要训练的树的数量。
• objective：定义学习任务和相应的学习目标。
• nthread：并行化的线程数。

5. 训练模型

使用xgboost.train函数来训练模型：

params = {
    'max_depth': 3,  # 树的最大深度
    'eta': 0.3,      # 学习率
    'objective': 'binary:logistic'  # 目标函数
}

bst = xgboost.train(params, dtrain, num_boost_round=100)

在这里，num_boost_round是迭代次数，即要构建的树的数量。

6. 模型预测

使用训练好的模型进行预测：

preds = bst.predict(dtest)

7. 模型评估

评估模型的性能，可以使用不同的指标，如准确率、AUC等：

from sklearn.metrics import accuracy_score

accuracy = accuracy_score(y_test, preds)
print(f"Accuracy: {accuracy}")

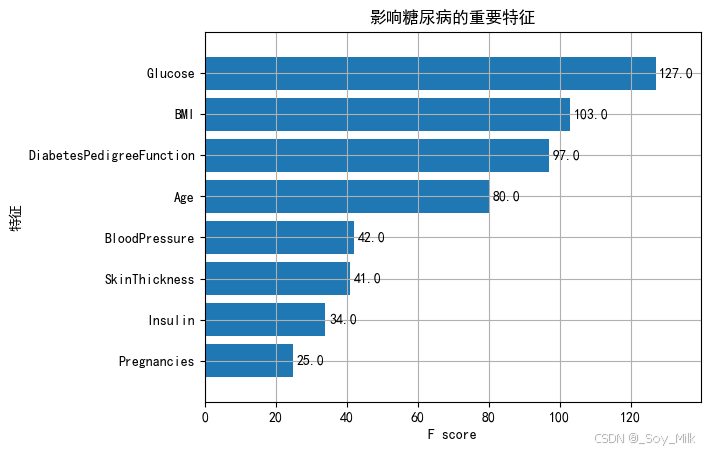
8. 特征重要性

XGBoost还提供了特征重要性的功能，可以用来理解哪些特征对模型的预测最为重要：

import matplotlib.pyplot as plt

xgb.plot_importance(bst)
plt.show()

9. 保存和加载模型

你可以保存训练好的模型，并在以后重新加载它：

bst.save_model('model.json')  # 保存模型
bst = xgboost.Booster()       # 加载模型
bst.load_model('model.json')

10. 调参

使用交叉验证和网格搜索等技术来找到最佳的参数组合。

五、决策树的使用场景：

• 决策树和随机森林通常适用于结构化数据，也称为表格数据。

• 决策树和随机森林不适用于非结构数据（如：图像，声音）。

实验部分：

一、导入相关库

import math
import numpy as np 

二、创建数据集

# 创建信贷数据集
def createDataLH():
    data = np.array([['青年', '否', '否', '一般']])
    data = np.append(data, [['青年', '否', '否', '好']], axis = 0)
    data = np.append(data, [['青年', '是', '否', '好'] 
                            , ['青年', '是', '是', '一般']
                            , ['青年', '否', '否', '一般']
                            , ['中年', '否', '否', '一般']
                            , ['中年', '否', '否', '好']
                            , ['中年', '是', '是', '好']
                            , ['中年', '否', '是', '非常好']
                            , ['中年', '否', '是', '非常好']
                            , ['老年', '否', '是', '非常好']
                            , ['老年', '否', '是', '好']
                            , ['老年', '是', '否', '好']
                            , ['老年', '是', '否', '非常好']
                            , ['老年', '否', '否', '一般']
                           ], axis = 0)
    label = np.array(['否', '否', '是', '是', '否', '否', '否', '是', '是', '是', '是', '是', '是', '是', '否'])
    label = ['借' if i == '是' else '不借' for i in label]
    name = np.array(['年龄', '有工作', '有房子', '信贷情况'])
    return data, label, name

# 创建西瓜数据集
def createDataXG20():
    data = np.array([['青绿', '蜷缩', '浊响', '清晰', '凹陷', '硬滑']
                    , ['乌黑', '蜷缩', '沉闷', '清晰', '凹陷', '硬滑']
                    , ['乌黑', '蜷缩', '浊响', '清晰', '凹陷', '硬滑']
                    , ['青绿', '蜷缩', '沉闷', '清晰', '凹陷', '硬滑']
                    , ['浅白', '蜷缩', '浊响', '清晰', '凹陷', '硬滑']
                    , ['青绿', '稍蜷', '浊响', '清晰', '稍凹', '软粘']
                    , ['乌黑', '稍蜷', '浊响', '稍糊', '稍凹', '软粘']
                    , ['乌黑', '稍蜷', '浊响', '清晰', '稍凹', '硬滑']
                    , ['乌黑', '稍蜷', '沉闷', '稍糊', '稍凹', '硬滑']
                    , ['青绿', '硬挺', '清脆', '清晰', '平坦', '软粘']
                    , ['浅白', '硬挺', '清脆', '模糊', '平坦', '硬滑']
                    , ['浅白', '蜷缩', '浊响', '模糊', '平坦', '软粘']
                    , ['青绿', '稍蜷', '浊响', '稍糊', '凹陷', '硬滑']
                    , ['浅白', '稍蜷', '沉闷', '稍糊', '凹陷', '硬滑']
                    , ['乌黑', '稍蜷', '浊响', '清晰', '稍凹', '软粘']
                    , ['浅白', '蜷缩', '浊响', '模糊', '平坦', '硬滑']
                    , ['青绿', '蜷缩', '沉闷', '稍糊', '稍凹', '硬滑']])
    label = np.array(['是', '是', '是', '是', '是', '是', '是', '是', '否', '否', '否', '否', '否', '否', '否', '否', '否'])
    name = np.array(['色泽', '根蒂', '敲声', '纹理', '脐部', '触感'])
    return data, label, name

# 切分训练集与验证集
def splitXgData20(xgData, xgLabel):   
    xgDataTrain = xgData[[0, 1, 2, 5, 6, 9, 13, 14, 15, 16],:]
    xgDataTest = xgData[[3, 4, 7, 8, 10, 11, 12],:]
    xgLabelTrain = xgLabel[[0, 1, 2, 5, 6, 9, 13, 14, 15, 16]]
    xgLabelTest = xgLabel[[3, 4, 7, 8, 10, 11, 12]]
    return xgDataTrain, xgLabelTrain, xgDataTest, xgLabelTest

三、函数功能测试

lhData, lhLabel, lhName = createDataLH()
print("书中值为0.971，函数结果：" + str(round(singleEntropy(lhLabel), 3)))  
print("书中值为0.083，函数结果：" + str(round(infoGain(lhData[:,0] ,lhLabel), 3)))  
print("书中值为0.324，函数结果：" + str(round(infoGain(lhData[:,1] ,lhLabel), 3)))  
print("书中值为0.420，函数结果：" + str(round(infoGain(lhData[:,2] ,lhLabel), 3)))  
print("书中值为0.363，函数结果：" + str(round(infoGain(lhData[:,3] ,lhLabel), 3)))  

xgData, xgLabel, xgName = createDataXG20()
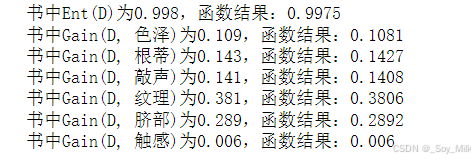
print("书中Ent(D)为0.998，函数结果：" + str(round(singleEntropy(xgLabel), 4)))  
print("书中Gain(D, 色泽)为0.109，函数结果：" + str(round(infoGain(xgData[:,0] ,xgLabel), 4)))  
print("书中Gain(D, 根蒂)为0.143，函数结果：" + str(round(infoGain(xgData[:,1] ,xgLabel), 4)))  
print("书中Gain(D, 敲声)为0.141，函数结果：" + str(round(infoGain(xgData[:,2] ,xgLabel), 4)))  
print("书中Gain(D, 纹理)为0.381，函数结果：" + str(round(infoGain(xgData[:,3] ,xgLabel), 4)))  
print("书中Gain(D, 脐部)为0.289，函数结果：" + str(round(infoGain(xgData[:,4] ,xgLabel), 4)))  
print("书中Gain(D, 触感)为0.006，函数结果：" + str(round(infoGain(xgData[:,5] ,xgLabel), 4)))  

四、创建树生成相关函数

# 特征选取，选取最好的特征，返回特征索引以及评价指标值
def bestFeature(data, labels, method = 'id3'):
    assert method in ['id3', 'c45'], "method 须为id3或c45"
    data = np.asarray(data)
    labels = np.asarray(labels)
    # 根据输入的method选取 评估特征的方法：id3 -> 信息增益; c45 -> 信息增益率
    def calcEnt(feature, labels):
        if method == 'id3':
            return infoGain(feature, labels)
        elif method == 'c45' :
            return infoGainRatio(feature, labels)
    # 特征数量  即 data 的列数量
    featureNum = data.shape[1]
    # 计算最佳特征
    bestEnt = 0 
    bestFeat = -1    # 最好的特征的索引
    for feature in range(featureNum):
        ent = calcEnt(data[:, feature], labels)
        if ent >= bestEnt:
            bestEnt = ent 
            bestFeat = feature
        # print("feature " + str(feature + 1) + " ent: " + str(ent)+ "\t bestEnt: " + str(bestEnt))
    return bestFeat, bestEnt 


# 根据特征及特征值分割原数据集  删除data中的feature列，并根据feature列中的值分割 data和label，返回的是字典类型的数据
def splitFeatureData(data, labels, feature):
    """feature 为特征列的索引"""
    # 取特征列
    features = np.asarray(data)[:,feature]
    # 数据集中删除特征列
    data = np.delete(np.asarray(data), feature, axis = 1)
    # 标签
    labels = np.asarray(labels)
    
    uniqFeatures = set(features)
    dataSet = {}
    labelSet = {}
    for feat in uniqFeatures:
        dataSet[feat] = data[features == feat]    # 使用字典来模拟树的划分
        labelSet[feat] = labels[features == feat]
    return dataSet, labelSet
    
    
# 多数投票， 返回投票最多的label，代表某一节点最终属于的标签
def voteLabel(labels):
    uniqLabels = list(set(labels))
    labels = np.asarray(labels)

    finalLabel = 0
    labelNum = []
    for label in uniqLabels:
        # 统计每个标签值的数量
        labelNum.append(equalNums(labels, label))
    # 返回数量最多的标签
    return uniqLabels[labelNum.index(max(labelNum))]


# 创建决策树
def createTree(data, labels, names, method = 'id3'):
    '''
    以字典来模拟树：{'特征1': {"特征1的第一种值": "叶子节点对应的标签", "特征1的第二种值": {"特征2":{...}}}
    '''
    data = np.asarray(data)
    labels = np.asarray(labels)
    names = np.asarray(names)
    # 如果结果为单一结果
    if len(set(labels)) == 1: 
        return labels[0] 
    # 如果没有待分类特征，所有的特征均被分完，进行投票选举该node所属的标签
    elif data.size == 0: 
        return voteLabel(labels)
    
    # 其他情况则选取特征 
    bestFeat, bestEnt = bestFeature(data, labels, method = method)
    # 取特征名称
    bestFeatName = names[bestFeat]
    # 从特征名称列表删除已取得特征名称
    names = np.delete(names, [bestFeat])
    # 根据选取的特征名称创建树节点
    decisionTree = {bestFeatName: {}}
    # 根据最优特征进行分割
    dataSet, labelSet = splitFeatureData(data, labels, bestFeat)
    
    # 对最优特征的每个特征值所分的数据子集进行计算，递归调用
    for featValue in dataSet.keys():
        decisionTree[bestFeatName][featValue] = createTree(dataSet.get(featValue), labelSet.get(featValue), names, method)
    return decisionTree 


# 树信息统计 叶子节点数量 和 树深度
def getTreeSize(decisionTree):
    nodeName = list(decisionTree.keys())[0]
    nodeValue = decisionTree[nodeName]
    leafNum = 0
    treeDepth = 0 
    leafDepth = 0
    
    # 进行递归调用求叶子节点的数量，以及树的深度
    for val in nodeValue.keys():
        if type(nodeValue[val]) == dict:
            leafNum += getTreeSize(nodeValue[val])[0]
            leafDepth = 1 + getTreeSize(nodeValue[val])[1] 
        else :
            leafNum += 1 
            leafDepth = 1 
        treeDepth = max(treeDepth, leafDepth)
    return leafNum, treeDepth 


# 使用模型对其他数据分类，验证其它数据
def dtClassify(decisionTree, rowData, names):
    names = list(names)
    # 获取当前深度的所有特征
    feature = list(decisionTree.keys())[0]
    # 决策树对于该特征的值的判断字段
    featDict = decisionTree[feature]
    # 获取特征对应名称的索引
    feat = names.index(feature)
    # 获取数据该特征的值
    featVal = rowData[feat]
    # 根据特征值查找结果，如果结果是字典说明是子树，调用本函数递归，否则的话是叶子节点，返回叶子节点的标签。
    if featVal in featDict.keys():
        if type(featDict[featVal]) == dict:
            classLabel = dtClassify(featDict[featVal], rowData, names)
        else:
            classLabel = featDict[featVal] 
    return classLabel

五、树可视化

import matplotlib.pyplot as plt 
plt.rcParams['font.sans-serif'] = ['SimHei']  # 指定默认字体为黑体
plt.rcParams['axes.unicode_minus'] = False  # 解决负号'-'显示为方块的问题


decisionNodeStyle = dict(boxstyle = "sawtooth", fc = "0.8")
leafNodeStyle = {"boxstyle": "round4", "fc": "0.8"}
arrowArgs = {"arrowstyle": "<-"}


# 画节点
def plotNode(nodeText, centerPt, parentPt, nodeStyle):
    createPlot.ax1.annotate(nodeText, xy = parentPt, xycoords = "axes fraction", xytext = centerPt
                            , textcoords = "axes fraction", va = "center", ha="center", bbox = nodeStyle, arrowprops = arrowArgs)


# 添加箭头上的标注文字
def plotMidText(centerPt, parentPt, lineText):
    xMid = (centerPt[0] + parentPt[0]) / 2.0
    yMid = (centerPt[1] + parentPt[1]) / 2.0 
    createPlot.ax1.text(xMid, yMid, lineText)
    
    
# 画树
def plotTree(decisionTree, parentPt, parentValue):
    # 计算宽与高
    leafNum, treeDepth = getTreeSize(decisionTree) 
    # 在 1 * 1 的范围内画图，因此分母为 1
    # 每个叶节点之间的偏移量
    plotTree.xOff = plotTree.figSize / (plotTree.totalLeaf - 1)
    # 每一层的高度偏移量
    plotTree.yOff = plotTree.figSize / plotTree.totalDepth
    # 节点名称
    nodeName = list(decisionTree.keys())[0]
    # 根节点的起止点相同，可避免画线；如果是中间节点，则从当前叶节点的位置开始，
    #      然后加上本次子树的宽度的一半，则为决策节点的横向位置
    centerPt = (plotTree.x + (leafNum - 1) * plotTree.xOff / 2.0, plotTree.y)
    # 画出该决策节点
    plotNode(nodeName, centerPt, parentPt, decisionNodeStyle)
    # 标记本节点对应父节点的属性值
    plotMidText(centerPt, parentPt, parentValue)
    # 取本节点的属性值
    treeValue = decisionTree[nodeName]
    # 下一层各节点的高度
    plotTree.y = plotTree.y - plotTree.yOff
    # 绘制下一层
    for val in treeValue.keys():
        # 如果属性值对应的是字典，说明是子树，进行递归调用； 否则则为叶子节点
        if type(treeValue[val]) == dict:
            plotTree(treeValue[val], centerPt, str(val))
        else:
            plotNode(treeValue[val], (plotTree.x, plotTree.y), centerPt, leafNodeStyle)
            plotMidText((plotTree.x, plotTree.y), centerPt, str(val))
            # 移到下一个叶子节点
            plotTree.x = plotTree.x + plotTree.xOff
    # 递归完成后返回上一层
    plotTree.y = plotTree.y + plotTree.yOff
    
    
# 画出决策树
def createPlot(decisionTree):
    fig = plt.figure(1, facecolor = "white")
    fig.clf()
    axprops = {"xticks": [], "yticks": []}
    createPlot.ax1 = plt.subplot(111, frameon = False, **axprops)
    # 定义画图的图形尺寸
    plotTree.figSize = 1.5 
    # 初始化树的总大小
    plotTree.totalLeaf, plotTree.totalDepth = getTreeSize(decisionTree)
    # 叶子节点的初始位置x 和 根节点的初始层高度y
    plotTree.x = 0 
    plotTree.y = plotTree.figSize
    plotTree(decisionTree, (plotTree.figSize / 2.0, plotTree.y), "")
    plt.show()

六、使用示例数据进行测试

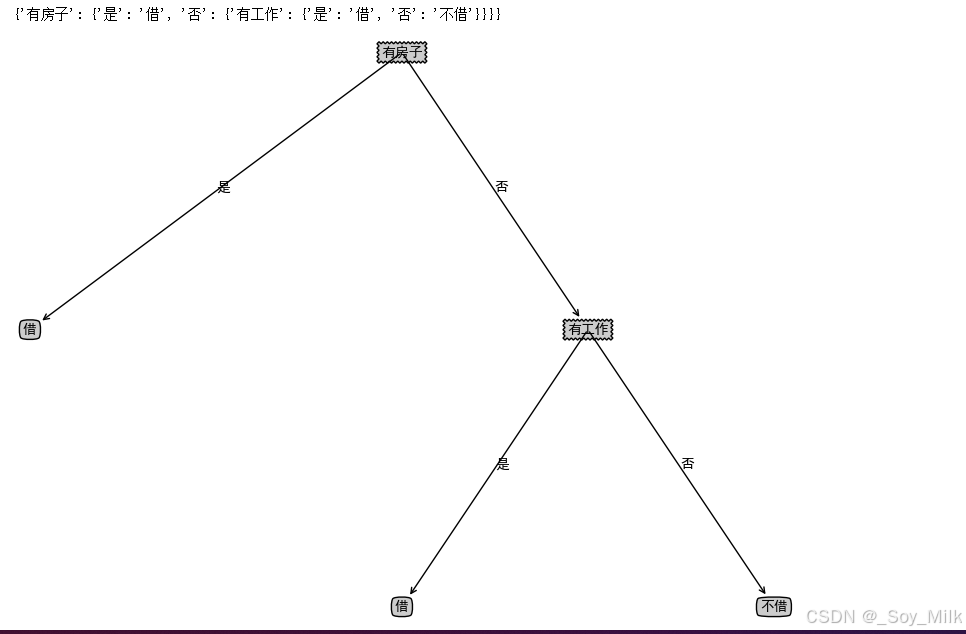
# 借贷数据集
lhData, lhLabel, lhName = createDataLH()
lhTree = createTree(lhData, lhLabel, lhName, method = 'id3')
print(lhTree)
createPlot(lhTree)

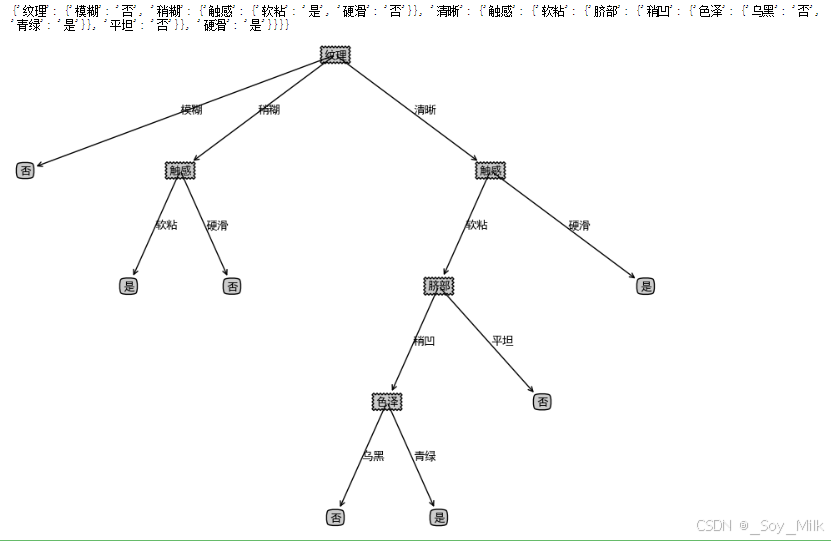
# 西瓜数据集
xgData, xgLabel, xgName = createDataXG20()
xgTree = createTree(xgData, xgLabel, xgName, method = 'id3')
print(xgTree)
createPlot(xgTree)

七、预剪枝

# 创建预剪枝决策树
def createTreePrePruning(dataTrain, labelTrain, dataTest, labelTest, names, method = 'id3'):
    """
    预剪枝 需要使用测试数据对每次的划分进行评估

    """
    trainData = np.asarray(dataTrain)
    labelTrain = np.asarray(labelTrain)
    testData = np.asarray(dataTest)
    labelTest = np.asarray(labelTest)
    names = np.asarray(names)
    # 如果结果为单一结果
    if len(set(labelTrain)) == 1: 
        return labelTrain[0] 
    # 如果没有待分类特征
    elif trainData.size == 0: 
        return voteLabel(labelTrain)
    
    # 其他情况则选取特征索引
    bestFeat, bestEnt = bestFeature(dataTrain, labelTrain, method = method)
    # 取特征名称
    bestFeatName = names[bestFeat]
    # 从特征名称列表删除已取得特征名称
    names = np.delete(names, [bestFeat])
    # 根据最优特征进行分割
    dataTrainSet, labelTrainSet = splitFeatureData(dataTrain, labelTrain, bestFeat)

    
    # 预剪枝评估
    # 划分前的分类标签
    labelTrainLabelPre = voteLabel(labelTrain)    # 进行选举
    labelTrainRatioPre = equalNums(labelTrain, labelTrainLabelPre) / labelTrain.size    # 得到选举标签数量占该节点总标签的比例
    # 划分后的精度计算 
    if dataTest is not None: 
        dataTestSet, labelTestSet = splitFeatureData(dataTest, labelTest, bestFeat)
        # 划分前的测试标签正确比例
        labelTestRatioPre = equalNums(labelTest, labelTrainLabelPre) / labelTest.size
        # 划分后 每个特征值的分类标签正确的数量
        labelTrainEqNumPost = 0
        for val in labelTrainSet.keys():
            labelTrainEqNumPost += equalNums(labelTestSet.get(val), voteLabel(labelTrainSet.get(val))) + 0.0
        # 划分后 正确的比例
        labelTestRatioPost = labelTrainEqNumPost / labelTest.size 
    
    # 如果没有评估数据 但划分前的精度等于最小值0.5 则继续划分
    if dataTest is None and labelTrainRatioPre == 0.5:
        decisionTree = {bestFeatName: {}}
        for featValue in dataTrainSet.keys():
            decisionTree[bestFeatName][featValue] = createTreePrePruning(dataTrainSet.get(featValue), labelTrainSet.get(featValue)
                                      , None, None, names, method)
    elif dataTest is None:
        return labelTrainLabelPre 
    # 如果划分后的精度相比划分前的精度下降, 则直接作为叶子节点返回
    elif labelTestRatioPost < labelTestRatioPre:
        return labelTrainLabelPre
    else :
        # 根据选取的特征名称创建树节点
        decisionTree = {bestFeatName: {}}
        # 对最优特征的每个特征值所分的数据子集进行计算
        for featValue in dataTrainSet.keys():
            decisionTree[bestFeatName][featValue] = createTreePrePruning(dataTrainSet.get(featValue), labelTrainSet.get(featValue)
                                      , dataTestSet.get(featValue), labelTestSet.get(featValue)
                                      , names, method)
    return decisionTree 

八、预剪枝测试

# 将西瓜数据分割为测试集和训练集
xgDataTrain, xgLabelTrain, xgDataTest, xgLabelTest = splitXgData20(xgData, xgLabel)
# 生成不剪枝的树
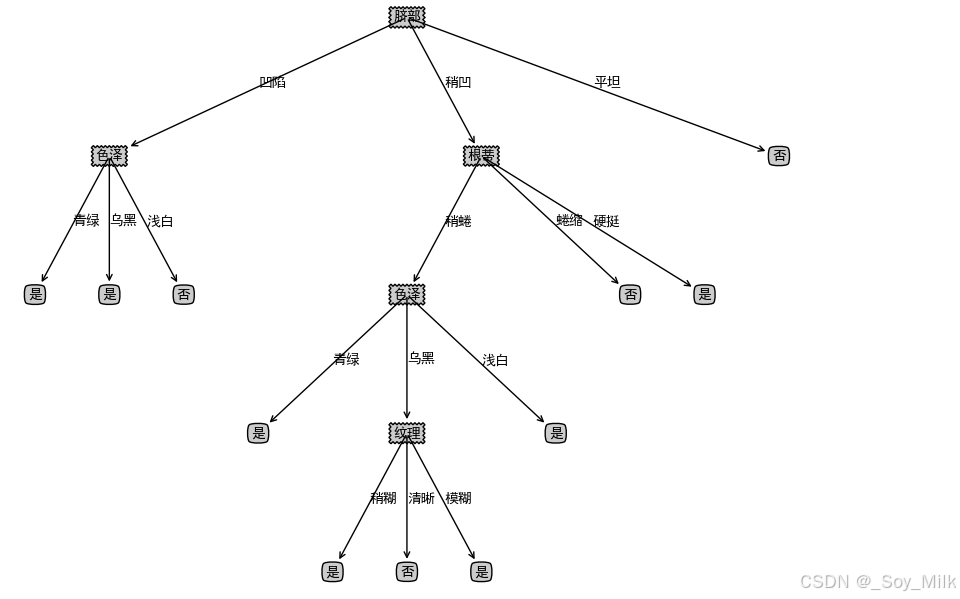
xgTreeTrain = createTree(xgDataTrain, xgLabelTrain, xgName, method = 'id3')
# 生成预剪枝的树
xgTreePrePruning = createTreePrePruning(xgDataTrain, xgLabelTrain, xgDataTest, xgLabelTest, xgName, method = 'id3')
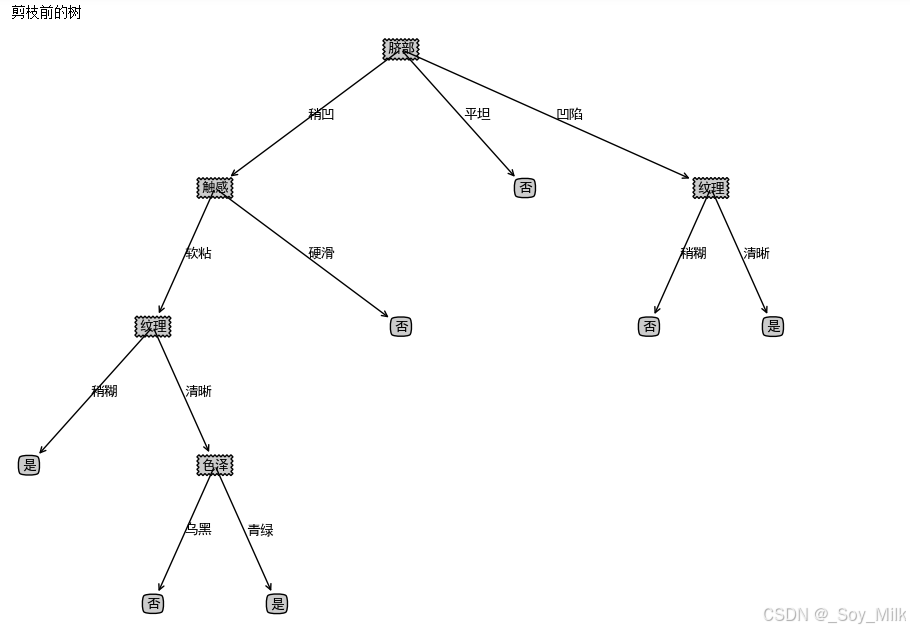
# 画剪枝前的树
print("剪枝前的树")
createPlot(xgTreeTrain)
# 画剪枝后的树
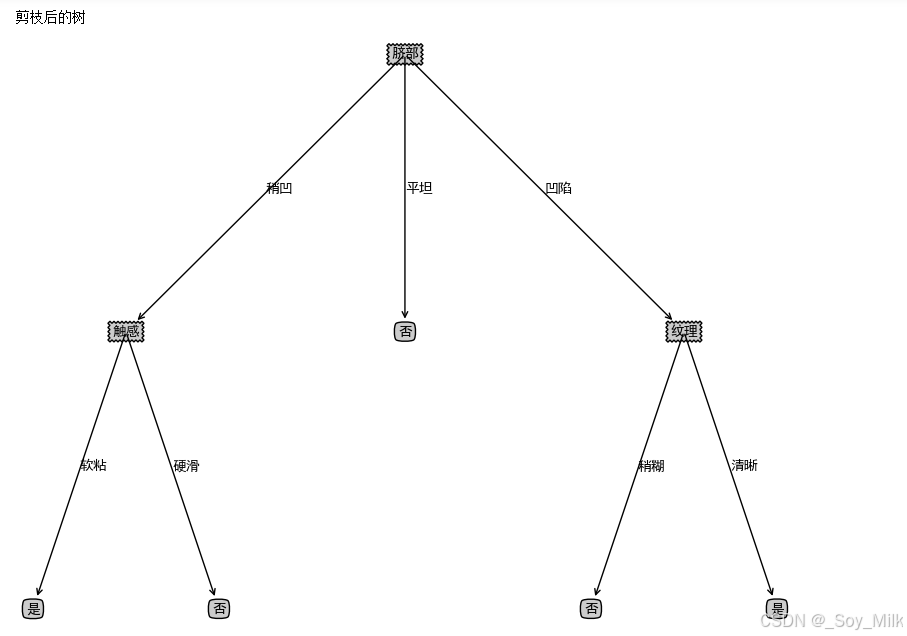
print("剪枝后的树")
createPlot(xgTreePrePruning)

九、后剪枝

改进训练函数，在训练的同时为每个节点增加划分前的标签，这样可以保证评估时只使用测试数据，避免再次使用大量的训练数据，写新的函数 createTreeWithLabel，当然也可以修改createTree来添加参数实现。

# 创建决策树 带预划分标签
def createTreeWithLabel(data, labels, names, method = 'id3'):
    data = np.asarray(data)
    labels = np.asarray(labels)
    names = np.asarray(names)
    # 如果不划分的标签为
    votedLabel = voteLabel(labels)
    # 如果结果为单一结果
    if len(set(labels)) == 1: 
        return votedLabel 
    # 如果没有待分类特征
    elif data.size == 0: 
        return votedLabel
    # 其他情况则选取特征 
    bestFeat, bestEnt = bestFeature(data, labels, method = method)
    # 取特征名称
    bestFeatName = names[bestFeat]
    # 从特征名称列表删除已取得特征名称
    names = np.delete(names, [bestFeat])
    # 根据选取的特征名称创建树节点 划分前的标签votedPreDivisionLabel=_vpdl
    decisionTree = {bestFeatName: {"_vpdl": votedLabel}}
    # 根据最优特征进行分割
    dataSet, labelSet = splitFeatureData(data, labels, bestFeat)
    # 对最优特征的每个特征值所分的数据子集进行计算
    for featValue in dataSet.keys():
        decisionTree[bestFeatName][featValue] = createTreeWithLabel(dataSet.get(featValue), labelSet.get(featValue), names, method)
    return decisionTree 


# 将带预划分标签的tree转化为常规的tree
# 函数中进行的copy操作，原因见有道笔记 【YL20190621】关于Python中字典存储修改的思考
def convertTree(labeledTree):
    labeledTreeNew = labeledTree.copy()
    nodeName = list(labeledTree.keys())[0]
    labeledTreeNew[nodeName] = labeledTree[nodeName].copy()
    for val in list(labeledTree[nodeName].keys()):
        if val == "_vpdl": 
            labeledTreeNew[nodeName].pop(val)
        elif type(labeledTree[nodeName][val]) == dict:
            labeledTreeNew[nodeName][val] = convertTree(labeledTree[nodeName][val])
    return labeledTreeNew


# 后剪枝 训练完成后决策节点进行替换评估  这里可以直接对xgTreeTrain进行操作
def treePostPruning(labeledTree, dataTest, labelTest, names):
    newTree = labeledTree.copy()
    dataTest = np.asarray(dataTest)
    labelTest = np.asarray(labelTest)
    names = np.asarray(names)
    # 取决策节点的名称 即特征的名称
    featName = list(labeledTree.keys())[0]
    # print("\n当前节点：" + featName)
    # 取特征的列
    featCol = np.argwhere(names==featName)[0][0]
    names = np.delete(names, [featCol])
    # print("当前节点划分的数据维度：" + str(names))
    # print("当前节点划分的数据：" )
    # print(dataTest)
    # print(labelTest)
    # 该特征下所有值的字典
    newTree[featName] = labeledTree[featName].copy()
    featValueDict = newTree[featName]
    featPreLabel = featValueDict.pop("_vpdl")
    # print("当前节点预划分标签：" + featPreLabel)
    # 是否为子树的标记
    subTreeFlag = 0
    # 分割测试数据 如果有数据 则进行测试或递归调用  np的array我不知道怎么判断是否None, 用is None是错的
    dataFlag = 1 if sum(dataTest.shape) > 0 else 0
    if dataFlag == 1:
        # print("当前节点有划分数据！")
        dataTestSet, labelTestSet = splitFeatureData(dataTest, labelTest, featCol)
    for featValue in featValueDict.keys():
        # print("当前节点属性 {0} 的子节点：{1}".format(featValue ,str(featValueDict[featValue])))
        if dataFlag == 1 and type(featValueDict[featValue]) == dict:
            subTreeFlag = 1 
            # 如果是子树则递归
            newTree[featName][featValue] = treePostPruning(featValueDict[featValue], dataTestSet.get(featValue), labelTestSet.get(featValue), names)
            # 如果递归后为叶子 则后续进行评估
            if type(featValueDict[featValue]) != dict:
                subTreeFlag = 0 
            
        # 如果没有数据  则转换子树
        if dataFlag == 0 and type(featValueDict[featValue]) == dict: 
            subTreeFlag = 1 
            # print("当前节点无划分数据！直接转换树："+str(featValueDict[featValue]))
            newTree[featName][featValue] = convertTree(featValueDict[featValue])
            # print("转换结果：" + str(convertTree(featValueDict[featValue])))
    # 如果全为叶子节点， 评估需要划分前的标签，这里思考两种方法，
    #     一是，不改变原来的训练函数，评估时使用训练数据对划分前的节点标签重新打标
    #     二是，改进训练函数，在训练的同时为每个节点增加划分前的标签，这样可以保证评估时只使用测试数据，避免再次使用大量的训练数据
    #     这里考虑第二种方法 写新的函数 createTreeWithLabel，当然也可以修改createTree来添加参数实现
    if subTreeFlag == 0:
        ratioPreDivision = equalNums(labelTest, featPreLabel) / labelTest.size
        equalNum = 0
        for val in labelTestSet.keys():
            equalNum += equalNums(labelTestSet[val], featValueDict[val])
        ratioAfterDivision = equalNum / labelTest.size 
        # print("当前节点预划分标签的准确率：" + str(ratioPreDivision))
        # print("当前节点划分后的准确率：" + str(ratioAfterDivision))
        # 如果划分后的测试数据准确率低于划分前的，则划分无效，进行剪枝，即使节点等于预划分标签
        # 注意这里取的是小于，如果有需要 也可以取 小于等于
        if ratioAfterDivision < ratioPreDivision:
            newTree = featPreLabel 
    return newTree

十、代码测试

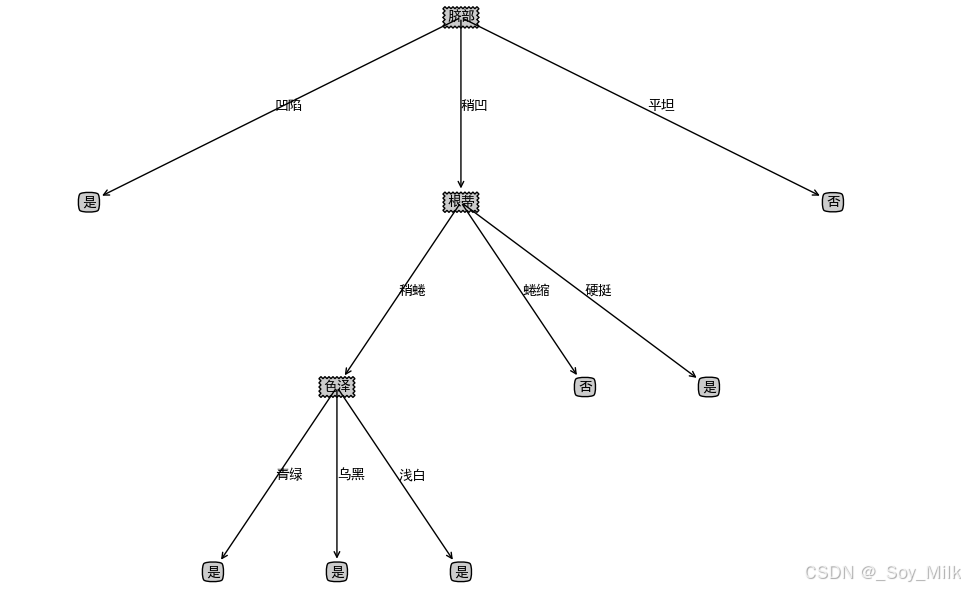
xgTreeBeforePostPruning = {"脐部": {"_vpdl": "是"
                                   , '凹陷': {'色泽':{"_vpdl": "是", '青绿': '是', '乌黑': '是', '浅白': '否'}}
                                   , '稍凹': {'根蒂':{"_vpdl": "是"
                                                  , '稍蜷': {'色泽': {"_vpdl": "是"
                                                                  , '青绿': '是'
                                                                  , '乌黑': {'纹理': {"_vpdl": "是"
                                                                               , '稍糊': '是', '清晰': '否', '模糊': '是'}}
                                                                  , '浅白': '是'}}
                                                  , '蜷缩': '否'
                                                  , '硬挺': '是'}}
                                   , '平坦': '否'}}
xgTreePostPruning = treePostPruning(xgTreeBeforePostPruning, xgDataTest, xgLabelTest, xgName)
createPlot(convertTree(xgTreeBeforePostPruning))
createPlot(xgTreePostPruning)

十一、XGBoost

import pandas as pd
from sklearn import metrics
from sklearn.model_selection import train_test_split
import xgboost as xgb
import matplotlib.pyplot as plt

# 导入数据集
df = pd.read_csv("diabetes.csv")
data=df.iloc[:,:8]
target=df.iloc[:,-1]
 
# 切分训练集和测试集
train_x, test_x, train_y, test_y = train_test_split(data,target,test_size=0.2,random_state=7)

# xgboost模型初始化设置
dtrain=xgb.DMatrix(train_x,label=train_y)
dtest=xgb.DMatrix(test_x)
watchlist = [(dtrain,'train')]

# booster:
params={'booster':'gbtree',
        'objective': 'binary:logistic',
        'eval_metric': 'auc',
        'max_depth':5,
        'lambda':10,
        'subsample':0.75,
        'colsample_bytree':0.75,
        'min_child_weight':2,
        'eta': 0.025,
        'seed':0,
        'nthread':8,
        'gamma':0.15,
        'learning_rate' : 0.01}

# 建模与预测：50棵树
bst=xgb.train(params,dtrain,num_boost_round=50,evals=watchlist)
ypred=bst.predict(dtest)
 
# 设置阈值、评价指标
y_pred = (ypred >= 0.5)*1
print ('Precesion: %.4f' %metrics.precision_score(test_y,y_pred,zero_division=0))
print ('Recall: %.4f' % metrics.recall_score(test_y,y_pred))
print ('F1-score: %.4f' %metrics.f1_score(test_y,y_pred))
print ('Accuracy: %.4f' % metrics.accuracy_score(test_y,y_pred))
print ('AUC: %.4f' % metrics.roc_auc_score(test_y,ypred))

ypred = bst.predict(dtest)
print("测试集每个样本的得分\n",ypred)
ypred_leaf = bst.predict(dtest, pred_leaf=True)
print("测试集每棵树所属的节点数\n",ypred_leaf)
ypred_contribs = bst.predict(dtest, pred_contribs=True)
print("特征的重要性\n",ypred_contribs )

xgb.plot_importance(bst,height=0.8,title='影响糖尿病的重要特征', ylabel='特征')
plt.rc('font', family='Arial Unicode MS', size=14)
plt.show()