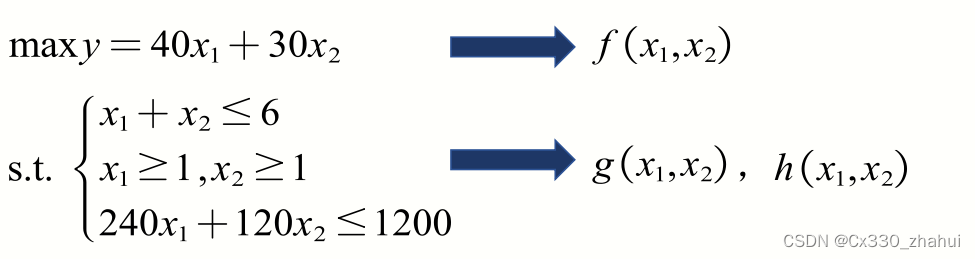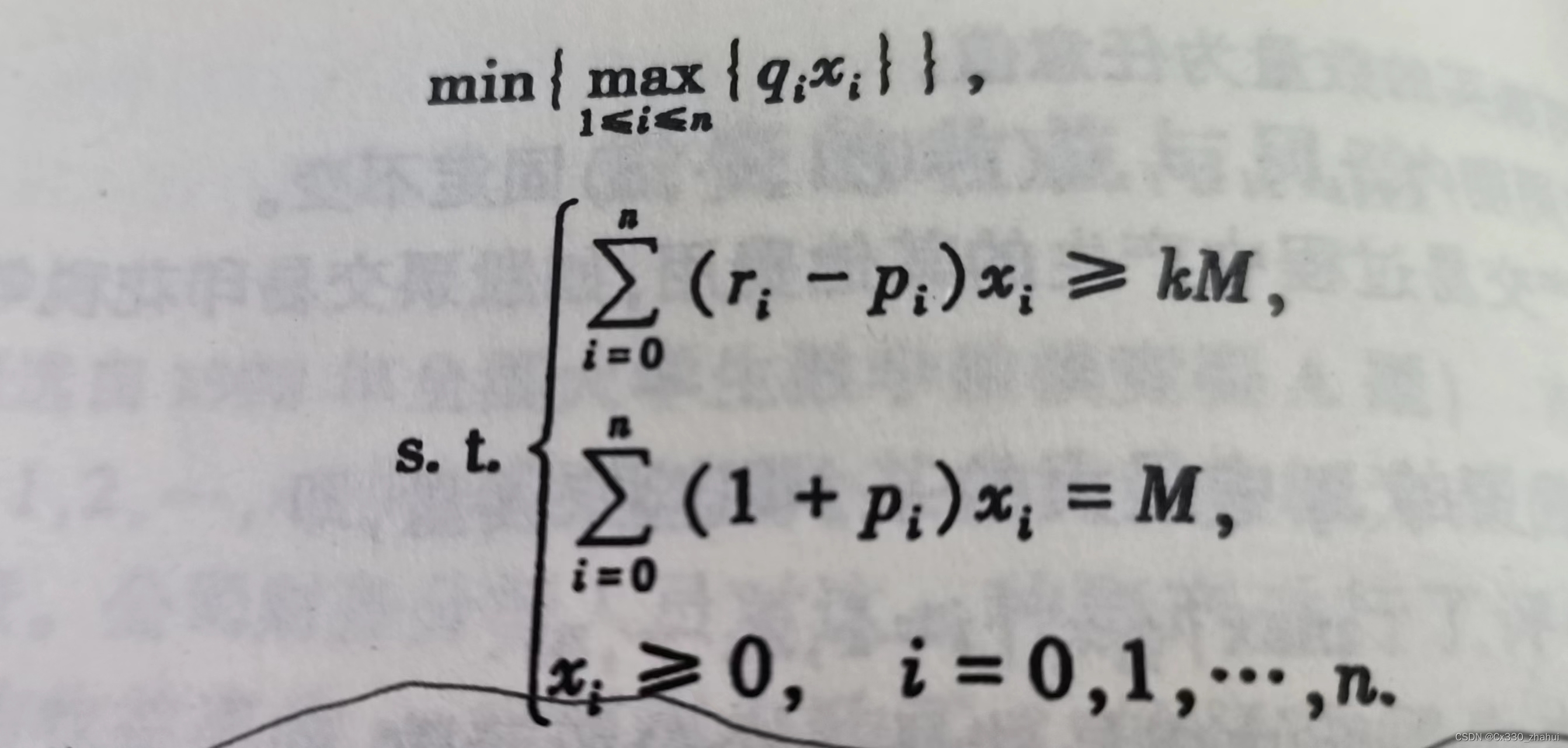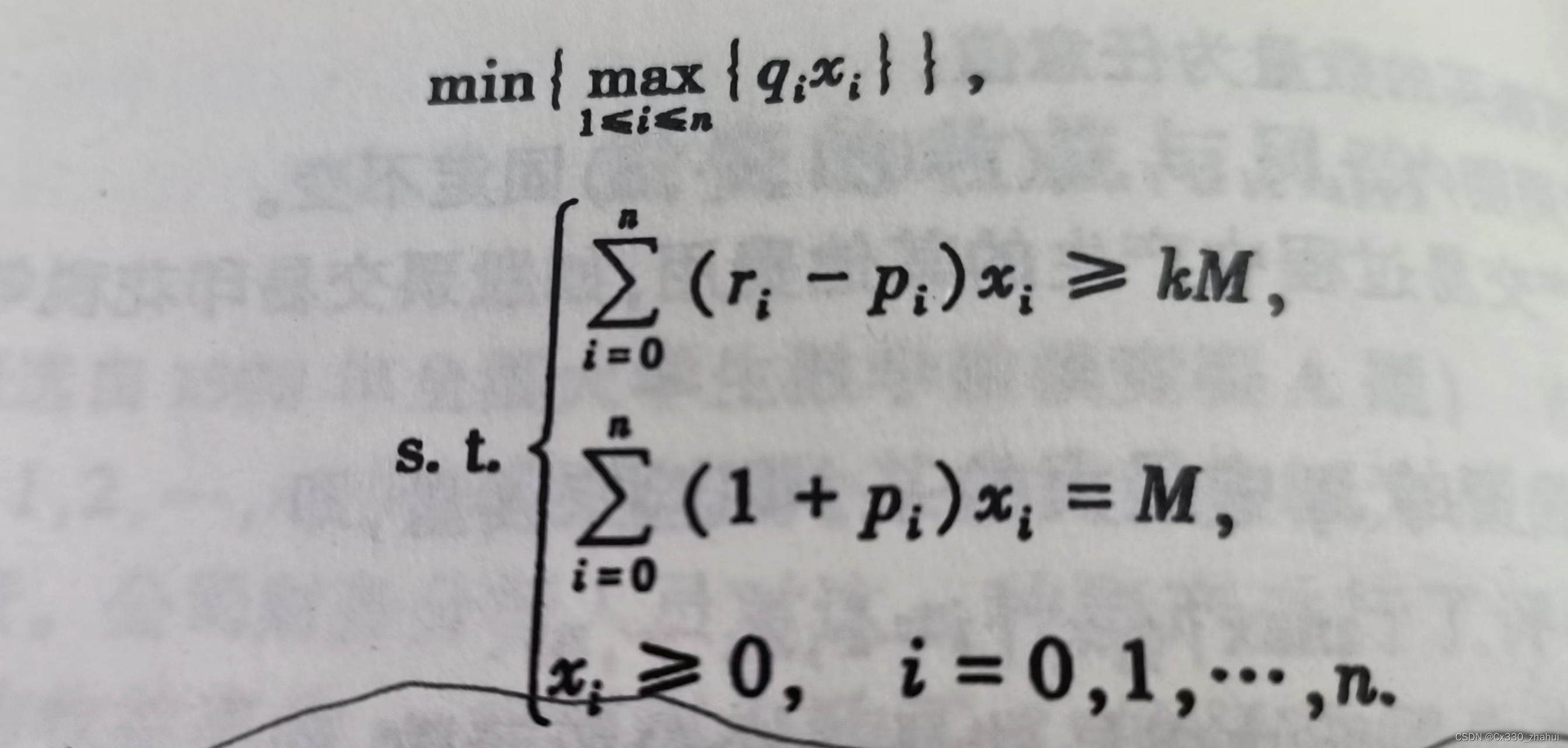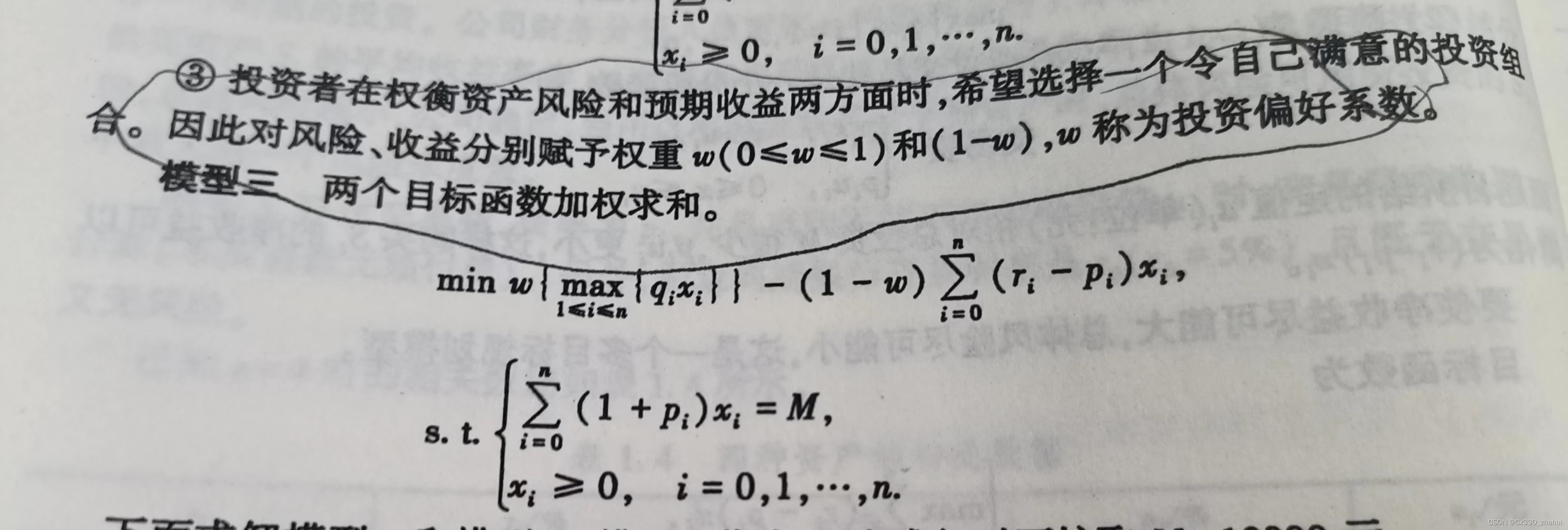1.1线性规划–介绍
翻译翻译什么叫惊喜
1.2线性规划–原理
拉格朗日乘数法手算
最值化
f
(
x
,
y
)
,
s
.
t
.
g
(
x
,
y
)
=
c
,
引入参数
λ
,有:
F
(
x
,
y
,
λ
)
=
f
(
x
,
y
)
+
λ
(
g
(
x
,
y
)
−
c
)
再将其分别对
x
,
y
,
λ
求导,求当其结果为
0
时,对应的值,即可求得驻点,分别带入目标函数即可得到最值。
最值化f(x,y), s.t.g(x,y) = c,引入参数λ,有: F(x,y,λ) = f(x,y) + λ(g(x,y) - c) 再将其分别对x,y,λ求导,求当其结果为0时,对应的值, 即可求得驻点,分别带入目标函数即可得到最值。
最值化f(x,y),s.t.g(x,y)=c,引入参数λ,有:F(x,y,λ)=f(x,y)+λ(g(x,y)−c)再将其分别对x,y,λ求导,求当其结果为0时,对应的值,即可求得驻点,分别带入目标函数即可得到最值。
1.3线性规划–定义
数学规划
数学规划是运筹学的一个分支,它用来研究在给定条件下(约束条件),如何按照一衡量指标(目标函数)来寻求计划、管理工作中的最优方案。
min(或者max)f(x), s.t. gi(x) <= 0 (如果是大于0的则要手动改为小于0)
这里x称为决策变量;f(x)称为目标函数; gi(x) <= 0称为约束条件。
线性规划---->如果f(x)和约束条件均为线性表达式,则此时就是线性规划。
1.4线性规划–应用
MATLAB的标准型要求
MATLAB的求解函数
[x,val] = linprog(f, A, b, Aeq, beq, lb, ub)
| 参数 | 解释说明 |
|---|---|
| f | 目标函数的系数列向量 |
| A,b | 不等式的系数矩阵和常数向量 |
| Aeq, beq | 等式的系数矩阵和常数向量 |
| lb,ub | 决策变量的最小值和最大值 |
| x | 取得目标函数最小值时x的取值 |
| val | 目标函数的最小值 |
| [] | 如果不存在某项约束则在对应位置填’[]’ |
| +inf,-inf | 若某个x无上下界则在对应矩阵上填此项 |
f = [-40;-30]
A = [1 1;240 120]
b = [6;1200]
lb = [1;1]
ub = [+inf;+inf]
[x,val] = linprog(f,A,b,[],[],lb,ub)
x =
4.0000
2.0000
val =
-220
上下界>=0时 为简化可以用如下方式代替lb,ub
c = zeros(2,1)
c =
0
0
>= 1 时 则为 ones()
书中内容补充
1.标准形式
2.绝对值参数转化为线性规划问题
min |x1| + |x2| + … +|xn|
s.t. Ax < = b
x = [x1,x2,…,xn]T
转化:对任意xi 存在ui ,vi >= 0 满足
xi = ui - vi , |xi| = ui + vi
只要取 ui = (xi + |xi|) /2 , vi = (xi - |xi|) /2
从而可以转化为
min ∑(ui + vi)
s.t. A(u - v) <= b u, v >= 0
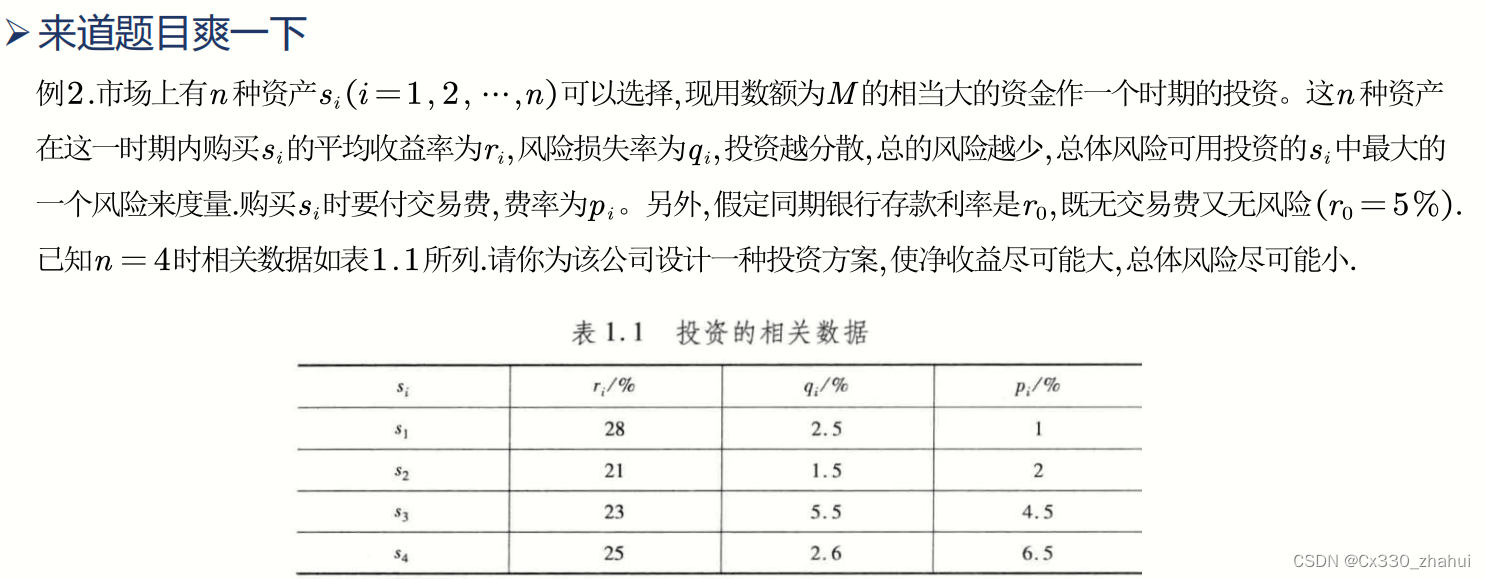
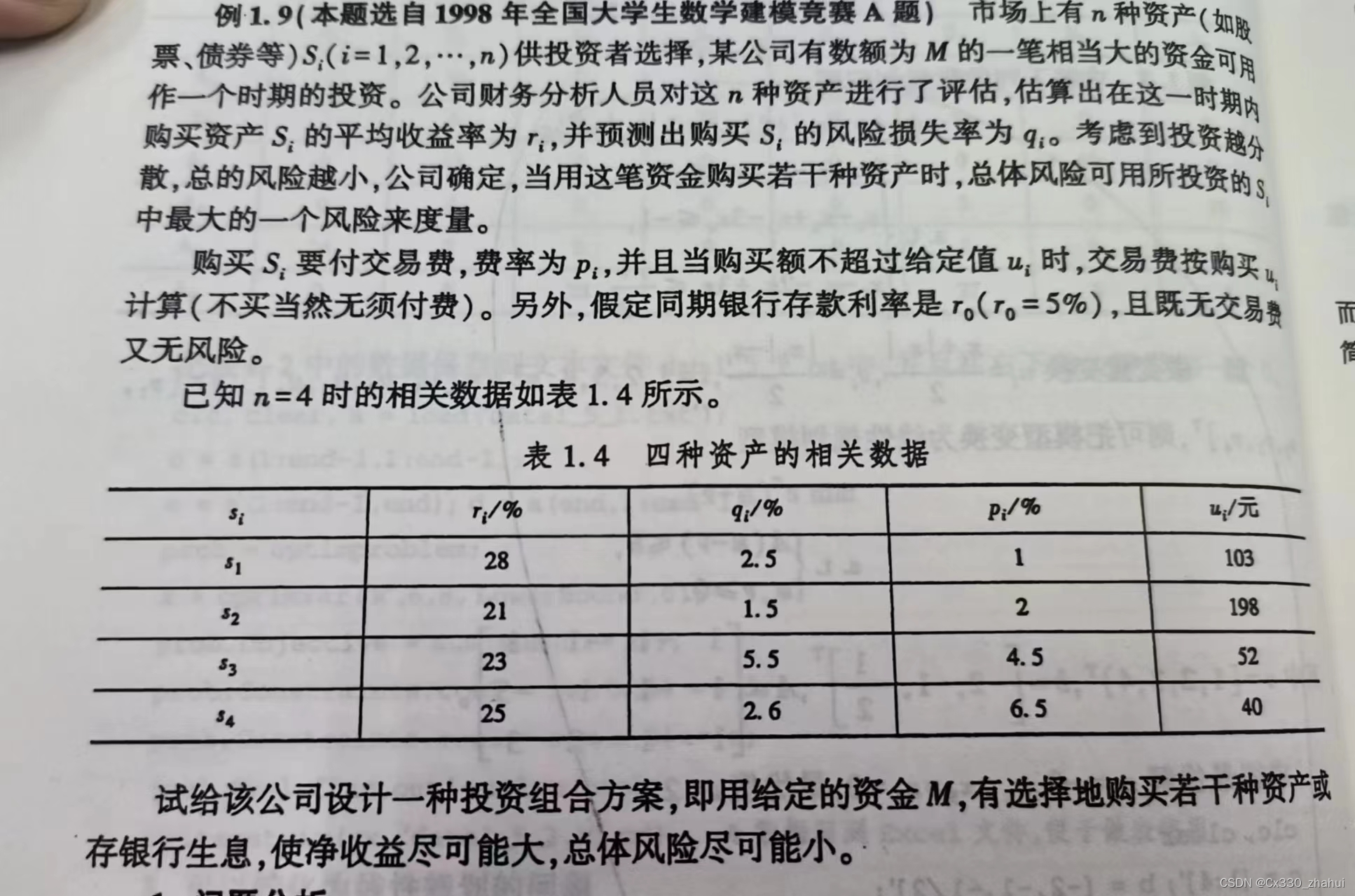
3.投资问题:收益与风险
3.1 问题分析:
3.2 模型一: 固定风险水平,优化收益
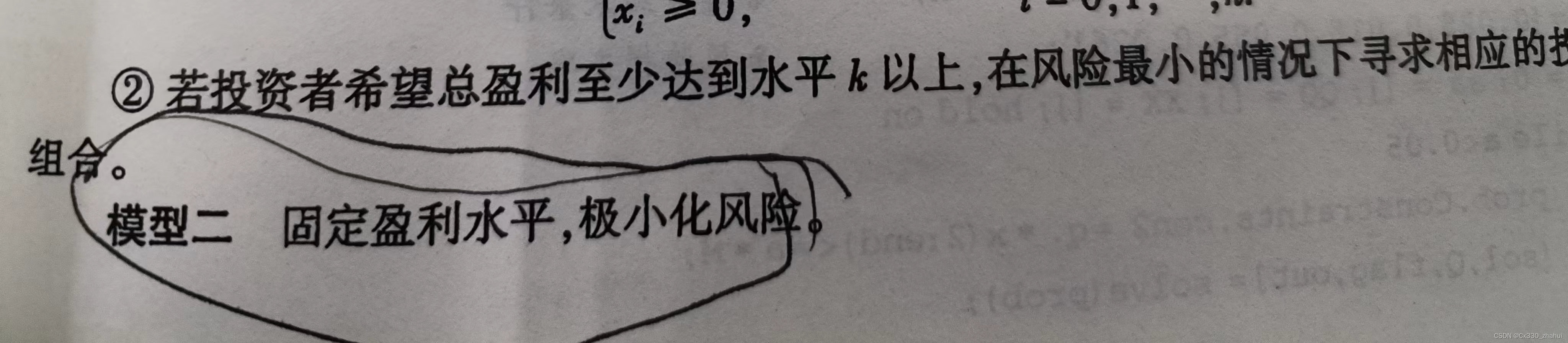
模型二: 固定盈利水平,极小化风险
模型三: 对风险和收益加权重 w,1-w