一、3种递归遍历方法
二叉树由3个基本单元组成:根结点、左子树和右子树。因此,若能依次遍历这三部分,便是遍历了整个二叉树。
假如以L、D、R分别表示遍历二叉树的方案,若限定先左后右则只有3中情况:
(1)先序遍历法:
先访问根结点,再先序遍历左子树,再是右子树。
如右图的二叉树,先序遍历法则输出:
1 2 5 6 3 4 7 8 9 10
(2)中序遍历法:
左子树 -> 根结点 -> 右子树
5 6 2 3 8 9 10 7 4 1
(3)后序遍历法:
左子树 -> 右子树 ->根结点
6 5 10 9 8 7 4 3 2 1
递归算法代码实现:
先序遍历法的代码如上,中序以及后序遍历法的代码类似,只需要把递归函数的位置调换即可。
void preOrderPrint(BiTreeNode* root)
{
if (root == NULL)
{
return;
}
printf("%d ", root->data);
preOrderPrint(root->leftChild);
preOrderPrint(root->rightBrother);
}
void printBiTree(BiTree bitree)
{
BiTreeNode* root = &bitree.btns[0];
preOrderPrint(root);
}注:考试不会考简单的递归算法,更多的是写出如何用堆栈的方法(非递归的方法)来实现。
仍然以先序遍历法为例:
void PreOrderTraversal_stack(BiTreeNode* root)
{
if (root == NULL)
{
return;
}
Stack stack;
initStack(&stack);
BiTreeNode* current = root;
while (current != NULL || !isEmpty(&stack))
{
while (current != NULL)
{
printf("%d ", current->data);
push(&stack, current);
current = current->leftChild;
}
if (!isEmpty(&stack))
{
current = pop(&stack);
current = current->rightBrother;
}
}
}其中,堆栈的定义和基本操作如下:
typedef struct StackNode
{
BiTreeNode* node;
struct StackNode* next;
} StackNode;
typedef struct Stack
{
StackNode* top;
} Stack;
//1、堆栈的初始化
void initStack(Stack* stack)
{
stack->top = NULL;
}
//2、判断堆栈是否为空
bool isEmpty(Stack* stack)
{
return stack->top == NULL;
}
//3、入栈
void push(Stack* stack, BiTreeNode* node)
{
StackNode* newNode = (StackNode*)malloc(sizeof(StackNode));
newNode->node = node;
newNode->next = stack->top;
stack->top = newNode;
}
//4、出栈
BiTreeNode* pop(Stack* stack)
{
if (stack->top == NULL)
{
return NULL;
}
BiTreeNode* node = stack->top->node;
StackNode* temp = stack->top;
stack->top = stack->top->next;
free(temp);
return node;
}二、层次遍历法
1. 定义一个队列,并把二叉树的根节点放入队列中。
2. 循环遍历队列,直到队列为空。
3. 在每一轮循环中,首先从队列中取出一个节点,并打印节点的值。
4. 如果该节点有左子树,则把左子树放入队列中。
5. 如果该节点有右子树,则把右子树放入队列中。
6. 重复步骤3-5,直到队列为空。
void levelOrderTraversal(BiTreeNode* root)
{
if (root == NULL)
{
return;
}
QueueNode* queue = NULL;
enqueue(&queue, root);
while (queue != NULL)
{
BiTreeNode* node = dequeue(&queue);
printf("%d ", node->data);
if (node->leftChild != NULL)
{
enqueue(&queue, node->leftChild);
}
if (node->rightBrother != NULL)
{
enqueue(&queue, node->rightBrother);
}
}
}其中enqueue是入队操作,dequeue是出队操作。二者定义如下:
// 入队操作
void enqueue(QueueNode** queue, BiTreeNode* node)
{
QueueNode* new_node = (QueueNode*)malloc(sizeof(QueueNode));
new_node->btn = node;
new_node->next = NULL;
if (*queue == NULL)
{
*queue = new_node;
}
else
{
QueueNode* curr = *queue;
while (curr->next != NULL)
{
curr = curr->next;
}
curr->next = new_node;
}
}
// 出队操作
BiTreeNode* dequeue(QueueNode** queue)
{
if (*queue == NULL)
{
return NULL;
}
BiTreeNode* node = (*queue)->btn;
QueueNode* temp = *queue;
*queue = (*queue)->next;
free(temp);
return node;
}可运行完整代码:下面这段代码利用parent数组创建一棵普通树,将树转换为孩子兄弟法表示的二叉树,并用层次遍历法打印这棵二叉树。
#include <stdio.h>
#include <stdlib.h>
#define MAX_SIZE 20
#define _CRT_SECURE_NO_WARNINGS
//定义树结构
typedef struct TreeNode
{
int data;
struct TreeNode* parent;
} TreeNode;
typedef struct Tree
{
TreeNode tns[MAX_SIZE];
int r, n;
} Tree;
Tree tree;
Tree tree2;
//定义二叉树结构
typedef struct BiTreeNode
{
int data;
struct BiTreeNode* leftChild;
struct BiTreeNode* rightBrother;
} BiTreeNode;
typedef struct BiTree
{
BiTreeNode btns[MAX_SIZE];
int r, n;
} BiTree;
BiTree bitree;
//定义队列结构及其操作
typedef struct QueueNode
{
BiTreeNode* btn;
struct QueueNode* next;
} QueueNode;
// 入队操作
void enqueue(QueueNode** queue, BiTreeNode* node);
// 出队操作
BiTreeNode* dequeue(QueueNode** queue);
Tree createTree(int parent[]);//用parent数组创建树
void findChild(BiTreeNode* root, Tree tree);//树转二叉树的辅助函数
BiTree treeToBiTree(Tree tree);//将树转换为二叉树
void levelOrderTraversal(BiTreeNode* root);// 层次顺序遍历二叉树
int main()
{
//1、传入parent数组
int parent[10] = { -1, 0, 0, 0, 1, 1, 3, 6, 6, 6 };
//2、创建树
Tree tree = createTree(parent);
//3、将树转换为二叉树
BiTree tree1 = treeToBiTree(tree);
//4、层次遍历法遍历二叉树
levelOrderTraversal(&tree1.btns[0]);
return 0;
}
void enqueue(QueueNode** queue, BiTreeNode* node)
{
QueueNode* new_node = (QueueNode*)malloc(sizeof(QueueNode));
new_node->btn = node;
new_node->next = NULL;
if (*queue == NULL)
{
*queue = new_node;
}
else
{
QueueNode* curr = *queue;
while (curr->next != NULL)
{
curr = curr->next;
}
curr->next = new_node;
}
}
BiTreeNode* dequeue(QueueNode** queue)
{
if (*queue == NULL)
{
return NULL;
}
BiTreeNode* node = (*queue)->btn;
QueueNode* temp = *queue;
*queue = (*queue)->next;
free(temp);
return node;
}
Tree createTree(int parent[])
{
tree.r = 0;
tree.n = 0;
while (tree.n < 10)
{
tree.tns[tree.n].data = tree.n + 1;
tree.tns[tree.n].parent = NULL;
if (parent[tree.n] != -1)
{
tree.tns[tree.n].parent = &tree.tns[parent[tree.n]];
}
tree.n++;
}
return tree;
}
void findChild(BiTreeNode* root, Tree tree)
{
BiTreeNode* currentChild = NULL;
for (int i = 0; i < tree.n; i++)
{
if (tree.tns[i].parent && tree.tns[i].parent->data == root->data)
{
BiTreeNode* newChild = &bitree.btns[i];
if (currentChild == NULL)
{
root->leftChild = newChild;
}
else
{
currentChild->rightBrother = newChild;
}
currentChild = newChild;
findChild(currentChild, tree);
}
}
}
BiTree treeToBiTree(Tree tree)
{
bitree.r = 0;
bitree.n = tree.n;
for (int i = 0; i < bitree.n; i++)
{
bitree.btns[i].data = tree.tns[i].data;
bitree.btns[i].leftChild = NULL;
bitree.btns[i].rightBrother = NULL;
}
BiTreeNode* root = &bitree.btns[0];
findChild(root, tree);
return bitree;
}
void levelOrderTraversal(BiTreeNode* root)
{
if (root == NULL)
{
return;
}
QueueNode* queue = NULL;
enqueue(&queue, root);
while (queue != NULL)
{
BiTreeNode* node = dequeue(&queue);
printf("%d ", node->data);
if (node->leftChild != NULL)
{
enqueue(&queue, node->leftChild);
}
if (node->rightBrother != NULL)
{
enqueue(&queue, node->rightBrother);
}
}
}
上述程序中利用parent数组创建的树以及转换成二叉树的形式如左图所示。
该二叉树用层次遍历法打印结果为:
1 2 5 3 6 4 7 8 9 10
与程序运行结果一致。
运行结果如下: 1 2 5 3 6 4 7 8 9 10 D:\Cfiles\DSweek8\Debug\DSweek8.exe (进程 19512)已退出,代码为 0。 按任意键关闭此窗口. . .
三、根据遍历结果创建二叉树
在遍历过程中生成结点,建立二叉树的存储结构。以先序遍历法为例,按照下列次序顺序读入字符:
A B C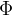
D E
G
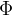
F
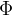
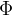
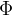
,其中表示空格字符,可以建立相应的二叉链表如左图。
代码实现
读入上文所给的字符串示例(先序遍历),创建二叉树,并打印中序遍历的结果。
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
#define MAX_NUM 20
typedef struct btNode
{
char data;
struct btNode* lChild;
struct btNode* rBrother;
}btNode;
btNode* createTree(FILE* fp);
void printTree(btNode* root);
int main()
{
char* filename = "D:\\Cfiles\\exFILE\\bTree_char.txt";
FILE* fp = fopen(filename, "r");
if (fp == NULL)
{
printf("打开文件错误");
return -1;
}
//1、读入字符文件创建二叉树
btNode* root = createTree(fp);
//2、打印二叉树信息
printTree(root);
fclose(fp);
return 0;
}
btNode* createTree(FILE* fp)
{
char ch;
fscanf(fp, "%c", &ch);
if (ch == ' ')
{
return NULL;
}
else
{
btNode* root = (btNode*)malloc(sizeof(btNode));
root->data = ch;
root->lChild = createTree(fp);
root->rBrother = createTree(fp);
return root;
}
}
void printTree(btNode* root)
{
if (root == NULL)
{
return;
}
printTree(root->lChild);
printf("%c ", root->data);
printTree(root->rBrother);
}运行结果:
C B E G D F A
D:\专业学习\大二下\DS\DSweek12\Debug\DSweek12.exe (进程 9728)已退出,代码为 0。
按任意键关闭此窗口. . .想法:
二叉树和图的遍历类似,深度优先/先根遍历这些都可以用堆栈代替递归算法,而宽度优先/层次遍历可以用队列。