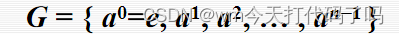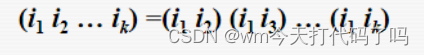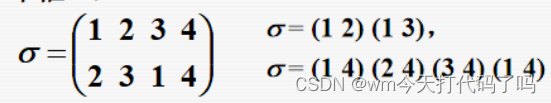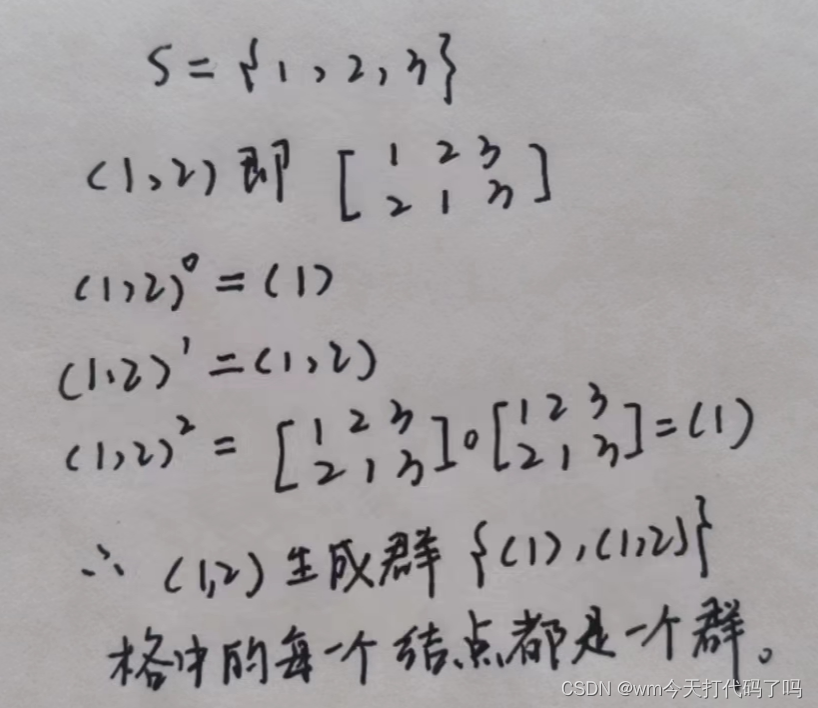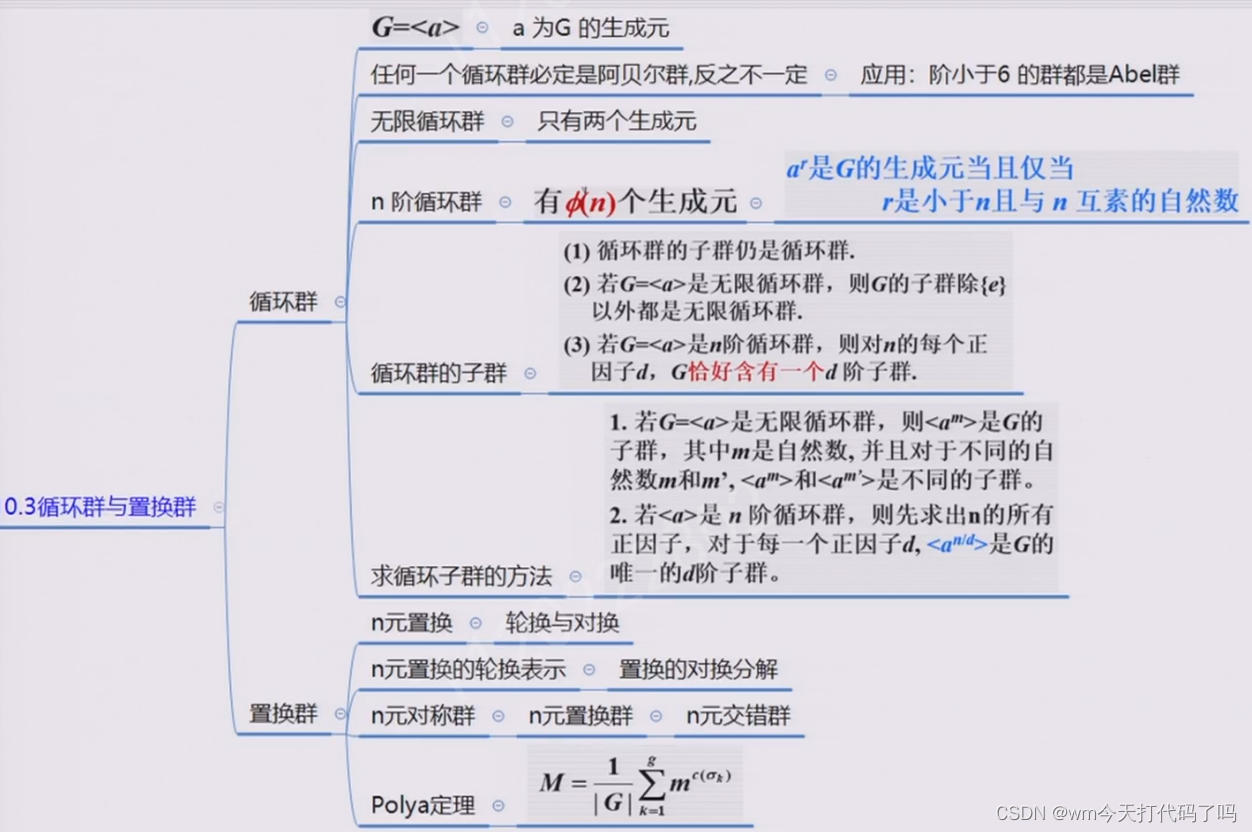
循环群

循环群定义和生成元

群G是由某一个元素生成的，具有循环的性质。若存在这样的元素，那么这个群就是循环群。

我突然就联想到上一节的生成子群？会不会有联系呢！

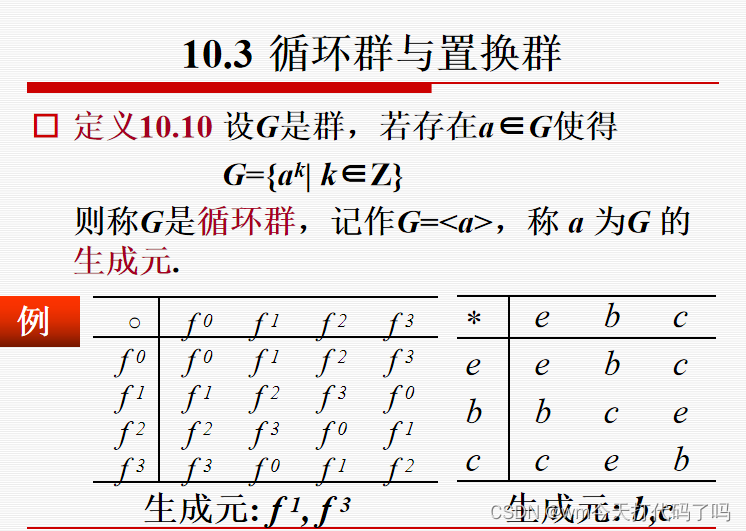
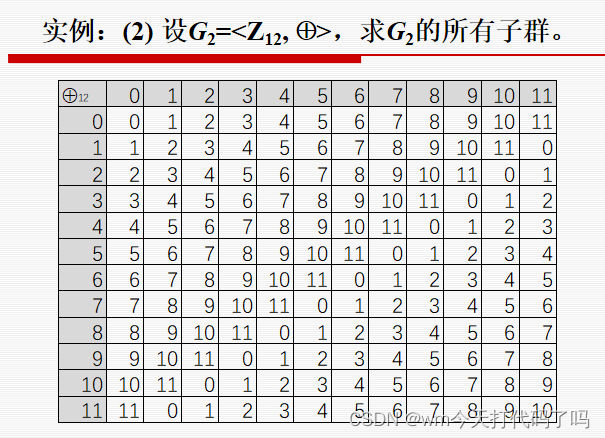
可以看到下面这张表，$f_1$的所有次幂构成的群就是一个循环群，结合上节课的内容，由$f_1$生成的G的子群，$f_1$就是生成元。同理$f_3$。

观察一个元素是不是生成元，只需要看这个元素的所有次幂是否能构成G中的所有元素。

看到这里！突然想到，构成生成子群的元素和生成元不一样！生成子群不一定包含了G的所有元素，而生成元生成的群必须就是G本身！

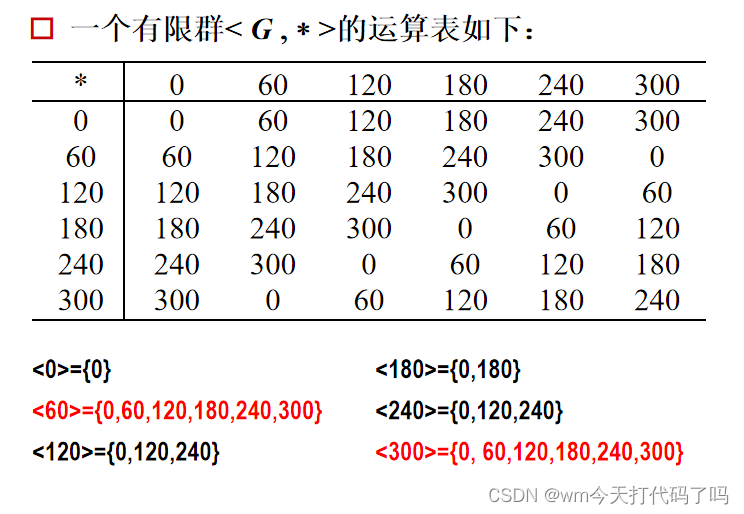
突然想起了上节课的角度旋转群——

可以看出只有60和300才是生成元。只有他们的所有次幂的运算结果能生成G本身。

到目前为止，我们只能通过计算出一个元素的所有次幂，看组成的集合是否构成G，来判断一个元素是不是生成元。（或许后面有更好的方法？）

定理

内容

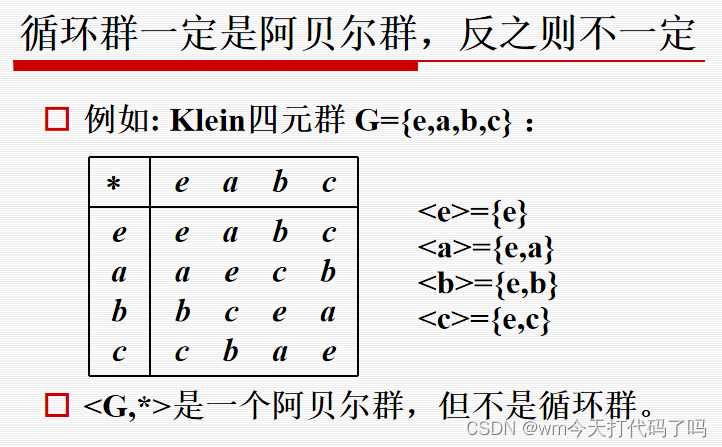
$$任意循环群必定是阿贝尔群，反之不一定$$
先不看证明，我们来思考一下：任意的一个群，这个群存在一个生成元a使得它的所有次幂的集合构成G，如果是阿贝尔群，那么它的所有元素都是可交换的，因为它的所有元素都是生成元a生成的，所以可以把任意的两个元素表示成a的形式来证明。

如果反过来呢？就不一定了。

Klein四元群是一个典型的阿贝尔群，但它不是循环群！

推论

$$阶小于6的群都是Abel群$$
证明：

• 1阶群中只含有e，一定是Abel群
• 2、3、5都是素数，因为素数的因子只有1和本身，因此素数阶群的生成子群的阶只可能是1或本身，即e或G本身（上节内容），是循环群，因此是Abel群
• 对于4阶群——
  

注意别忘记群中元素的阶是群阶的因子哦~

循环群的分类

这里提出了两个新的概念——n阶循环群和无限循环群。
对于n阶循环群G，它的生成元a进行幂运算进行到n次的时候，又返回了e。因此循环的周期是n，G中有n个元素。尤其注意——

定理（生成元的个数）

• 当G是无限阶群，例如整数加群。那么它的生成元就只有$a$和$a^{-1}$，由一个元素一直一直生成，生成无限个元素…
• 当G为n阶循环群，需要特殊考虑了。

上面这个欧拉函数记住结论即可。例如我们以上n=12的时候。注意上面那个小于或等于12似乎有点问题，不应该等于12，但其实结果是一样的，因为自己和自己不可能互素。

举两个例子：

这看起来是不是非常的神奇！！无限阶循环群只有两个生成元，找到了一个$a$就找到了另外一个$a^{-1}$，n阶循环群有$\varphi (n)$个生成元，其中$\varphi$是欧拉函数，$\varphi (n)$的值就是小于n的素数的个数，且这些生成元可以由$a^r$得出，其中r就是这些素数，a是其中一个生成元。

让我们来看看证明吧！
下面的证明看懂就行（看不懂记住也行考试不会考这个证明）——

先是无限循环群：

n阶循环群：
会用到一些数论的知识和定理，感兴趣可以去研究研究，可以直接拿来用。

根据以上定理及总结，有公式：$$a^n=e$$其中a是生成元。$$|a|=n$$因为n是使得$a^k$为e的最小正整数。又因为$a^r(r为小于n的素数)$也是生成元，所以$$|a^r|=n$$

好啦，以上的那些定理都会了吗，都记住了吗）循环群是什么！再来巩固一下——

• 有一个群G放在这里，如果G中存在一个元素ａ，求出ａ的所有整数次幂的结果，把这些结果组成集合，这个集合刚好是G，那么G就叫做循环群，ａ叫做生成元。这个生成元很特殊，是特殊的生成子群所用的元素。
• 如果G是ｎ阶循环群，那么生成元的阶是ｎ，即使得生成元的ｋ次幂等于ｅ的最小整数就是ｎ，由欧拉函数，$a^r$也是生成元，当然也有$|a^r|=n$，其中r是小于n的所有素数，n阶循环群生成元的个数就是小于n的所有素数的个数。
• 如果G是无限循环群，那么G只有两个生成元，一个$a$，一个$a^{-1}$。

ok我们继续——

循环群的子群

定理汇总
如果$G=<a>$是循环群，则

1. $G$的子群仍然是循环群
2. 若$G=<a>$是无限循环群，则G的子群除{e}以外都是无限循环群
3. 若$G=<a>$是n阶循环群，则对n的每个正因子d，G恰好含有一个d 阶子群

注意以上定理的前提条件！！母群G一定要是循环群！！

现在我们来一个一个的分析~

定理一

$$G的子群仍然是循环群$$
这就不得不又拿出前面的旋转群来进行辅助分析了：

这个群我们已经见过多次，它是一个典型的6阶循环群，存在元素60和300满足循环群存在条件。

如果要证明这个群G的子群仍然是循环群，我们要先找到它的子群：
$<0>$、$<60>$、$<120>$、$<240>$、$<300>$、$<360>$。（这些都是由G中元素生成的子群，但并不是所有的子群哦！生成子群并不是得到子群的唯一方式！）

找到了子群过后，就需要证明子群中存在某一个元素，求幂的所有结果的集合构成这个子群即可。
具体证明如下：

（注意前提，我们已经知道了a是生成元。）

定理二

$$若G=<a>是无限循环群，则G的子群除e以外都是无限循环群$$

定理三

$$若G=<a>是n阶循环群，则对n的每个正因子d，G恰好含有一个d阶子群$$

这个定理说明了：对于n阶循环群G，n的每一个正因子d，都对应了一个d阶子群。这个也可以由前面旋转群的例子看出规律。

求循环子群的方法

这个部分很重要，考试要考。
虽然用考试要考来考量一个部分是否重要是非常可悲的，但没办法，我们没有足够的时间和精力把所有的知识事无巨细全部弄清楚。

好了，拉回正题，敲黑板！这一块很重要，关键是要学会怎么用。

这两条定理列出了求循环群子群的方法，包括有限循环群和无限循环群。

例子
首先是无限循环群：

我想要求一个无限循环群G的子群，我就要先把它的生成元找到，然后求它的m次幂的生成群，这个群就是G的子群。当然循环群的子群也是循环群，我们之前讨论过这个问题。

然后是有限循环群：

这个群有5个生成元，我们就拿a=1来分析，其他的也是一样的。

我们要求一个有限的n阶循环群的子群，首先也要找到生成元a，然后求出n的所有正因子d，然后用$<a^{n/d}>$来生成群，这个群就是母群对应的唯一的$d$阶子群。

现在我们再来求一下旋转群的所有子群——
旋转群是一个6阶循环群，因此我们采取第二个方法。

现在我们敢说之前旋转群列出的生成子群就是所有的子群了！

循环群完结撒花❀❀❀~~

置换群

看完上述定义有点懵，停下来想想。置换是什么？置换就是对集合中元素的一个重新排列！但是这个排列不是任意的，它必须要满足一个双射关系，即：既要一一对应（单射），又要对于任意的陪域Y中的元素 y，在函数的定义域X中存在一点 x使得f (x)=y（满射）。

那么什么是n元置换呢，集合S中有多少个元素就叫几元置换。

如果置换后的每一个元素仍然等于原集合中的元素，就成为恒等置换。

群具有置换性质

群中的每一行每一列都是集合，他们具有置换性质。

解释一下：
对应于a的那一行，a与G中的每一个元素做运算，因为$a^{-1}b$一定是属于G的，所以$a$一定会与$a^{-1}b$做运算，得到的结果就是b，所以b一定会出现在a的那一行得证。而且只存在唯一一个这样的元素。

对列同理。

置换的乘法

不是真正意义上的乘法昂！！其实是复合运算！！

要注意的是，置换的乘法不满足交换律，小心哦~

轮换与对换

定义

注意这个k阶，轮换式子里有几个元素就是几阶轮换，当轮换式子里只有两个元素，就叫做对换。

这个直接看定义的话不容易理解，建议直接看例子再看定义——

例子

对于$\sigma$，1对应5，5对应4，4对应1，那么（1，5，4）就是一个轮换。同理，（2，3）也是一个轮换，很容易理解吧！当然，如果只有一个元素例如$\gamma$中遗留下了一个5，那么这个（5）自己就是一个轮换。

其中有一些注意点：

轮换分解式的特征

• 轮换分解式中的每一个括号里的元素和其他括号里的元素都是不相交的。
• 轮换分解的方式是唯一的。
• 1阶轮换可以省略，如果全是1阶轮换，那就只保留一个1阶轮换。

轮换分解式可以更加简洁地表达置换表达式，减少储存空间，当然也有很多其他的好处。

轮换的对换分解

对于置换，我们可以将其唯一表示成轮换，对于轮换，我们又可以将其唯一表示成对换。

这个相互表示方法是非常好的，因为把轮换拆成对换后，他们表示的仍然是同一个$\sigma$

注意这个式子：

方法就是拿轮换中的第一个元素与后面的元素一一配对~最后表示成对换的乘积。

对换分解的特征

最开始看这个$\sigma$居然还能表示成第二种形式！我想了好久，实际上是对换的本质没有搞清楚。
对于下面这个置换式子，可以表示成两种对换形式。首先表示成轮换为：$\sigma =(123)$
，然后分解成对换形式，就有了第一种对换分解式，$\sigma =(12)(13)$，它的实质意义就是将1234中的12先对换，成为2134，然后13对换，成为2314，就是置换后的式子。

那么同理第二种表示法如下面绿油油的图所示（差了一行自行脑补）

所以这就是为什么能表示成两种形式呢！而且你会发现，对换分解式里的元素是可交的（比如1和4同时出现在了好多个括号里），分解式不唯一。

对于奇置换和偶置换，就看对换分解式有几个括号，有奇数个括号，$\sigma$就是奇置换，有偶数个括号$\sigma$就是偶置换。

对换分解式可以有很多个，但奇偶性不变。

最后一个定理要记住！会出点小题。
任意一个n元置换中奇置换和偶置换的个数各有$$\frac{n!}{2}个$$

n元对称群

现在终于把话题又扯回了群，n元对称群！
对于一个集合$S$（有n个元素），所有的n元置换构成一个集合$S_n$，$S_n$再关于置换乘法构成群，这个群就叫做n元对称群。

n元对称群中的每个元素都是n元集合S的置换，元素个数一共有$$n!个$$即有$n!$个置换。

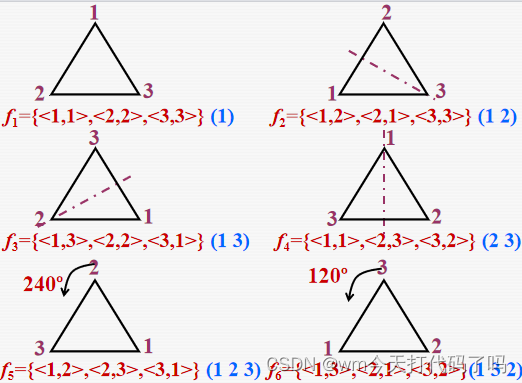
例如 S = { 1   2   3 } S = \{1\ 2\ 3\} S={1 2 3}，它的几种置换：恒等置换（1），（1 2），（1 3）等等，放在一个集合$S_n$里面，balbalabal…

不要被括号迷惑了，它只是一个简化置换的表示方法罢了。

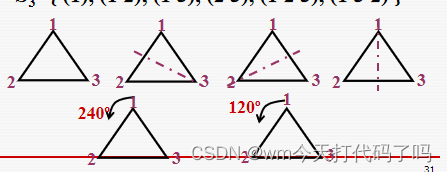
可以把上面的置换变换表示成三角形的旋转和翻转：



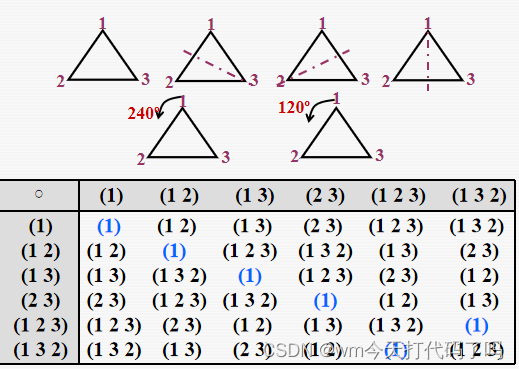
然后表示成群的运算表形式，注意这个运算是两个置换的复合运算，这里要拐一个弯。

注意一下这个群的特征：

• 首先是封闭的
• 每个元素都有逆，且（1）是单位元
• 是可交换的

n元对称群的概念有了，啊？不会已经忘了吧，什么是n元对称群？指的是对于一个集合S（有n个元素），将它的所有置换组成一个集合$S_n$，$S_n$以及关于置换的乘积运算组成的一个群，就叫做n元对称群，为什么叫做“对称”呢？因为根据置换的实际意义，可以将置换的过程表示为三角形的翻转和旋转，具有高度对称性。n元对称群的子群成为n元置换群。

n元交错群

看到这里，是不是忘了偶置换是什么！没关系，让我们回忆一下：
对于集合$S$，$\sigma$是$S$的一个置换，如果将$\sigma$可以表示成偶数个对换的乘积，那么$\sigma$就被称作为偶置换。

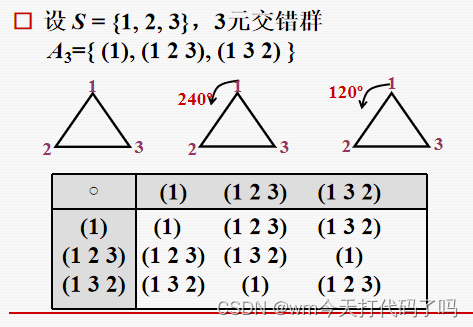
这里定义了一个$A_n$，是$S_n$（n元对称群）的一个子群，例如下面这个图，这里的$A_n=\{(1)(123)(132)\}$，很明显$A_n$是$S_n$的子群（沿用上面的$S_n$），而且满足里面的元素都是偶置换，所以$A_n$是一个3元交错群。

注意：恒等置换是偶置换，因为它可以表示成0个对换的乘积（0也是偶数是吧！！）

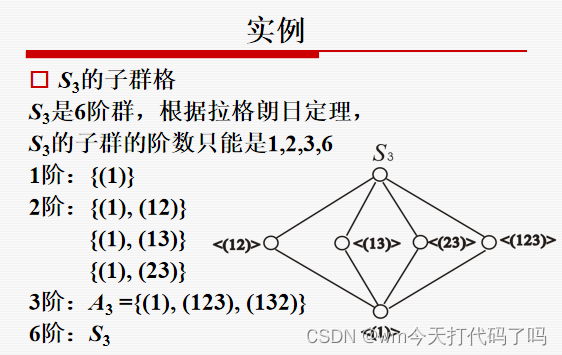
由此我们可以画出它的子群格：

小心！$S_3$并不意味着他就是3阶群！为什么是6阶呢？因为$S_3$有3个元素123，一共有$3!=6$个置换，这几个置换组成群，因此$S_3$是6阶群。

其中3阶子群是一个交错群（上面有提到过）；2阶子群有三个！联想起n阶循环群，用$<a^{n/d}>$来生成子群，（a是生成元），它只对应唯一一个d阶子群！这是很大的区别。当然，n元对称群也不是循环群，也不能用算循环群子群的方式来算子群。

注意一下这个子群格的表示方法！由上到下有一个包含（偏序）关系，$<(12)>$的意思是由$(12)$生成的一个群！这个$(12)$是一个置换，只是用对换的方式表示了出来。

关于格，后面会详细说到。

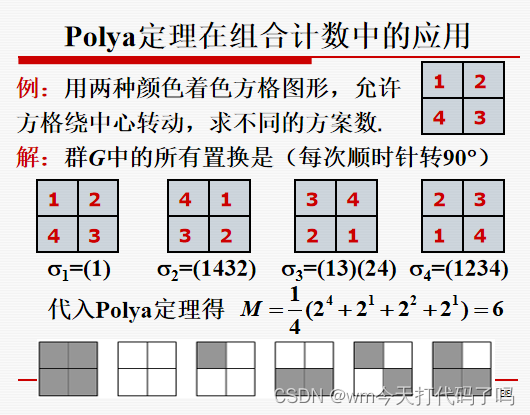
Polya定理

现在要用到置换群了！这个定理非常重要昂！需要你会用！记住这个结论，至于为什么，详见组合数学。

要记住这个公式：
$$M=\frac{1}{|G|}\sum _1^g{m}^{c({\sigma }_k)}$$

很难理解吧！直接上例题！

应用

注意这个$2^4$可能会卡一下，对于1234的恒等置换，表示成（1），但是实际上它是(1)(2)(3)(4)，所以说$c({\sigma }_k)$是4。（包含1阶轮换在内的轮换个数）

注意那个$|G|$，指的是n元置换群的阶数，即S的所有置换构成的群中元素的个数，在这道题里面就是4（如果按顺时针90°转动的话，有4种置换方式）。为什么是按顺时针90°转动呢！因为题目中说了允许绕方格的中心轴转动！那么我们就转吧哈哈哈。）如果不允许转动的话，那么置换就有4! = 24个！这个列出来要好多好多呀。

来一道升级题！！
现在不仅允许旋转了，甚至允许翻转了！

做这个题，只需要分别旋转、翻转，画出所有情况，数出置换的总个数与各种情况对应的轮换个数！

再来一个！！

这个题一般不考大题（当然也可能考！！）可能考填空题，它很耗时！！建议先跳过，后面再回来看。

来补充一点东西：
上面我们讲的都是3元对称群，如果是4元的呢？即$S_4$

把$S_4$的所有置换中偶置换挑出来，组成集合$A_n$，$A_n$就是一个交错群。

注意区别阶和元，例如8元置换群指的是集合S中有8个元素，8阶置换群指的是群中有8个置换。

总结：

循环群和置换群完结撒花❀❀❀~