题目： 

---

解析： 

部分决策树： 

 

---

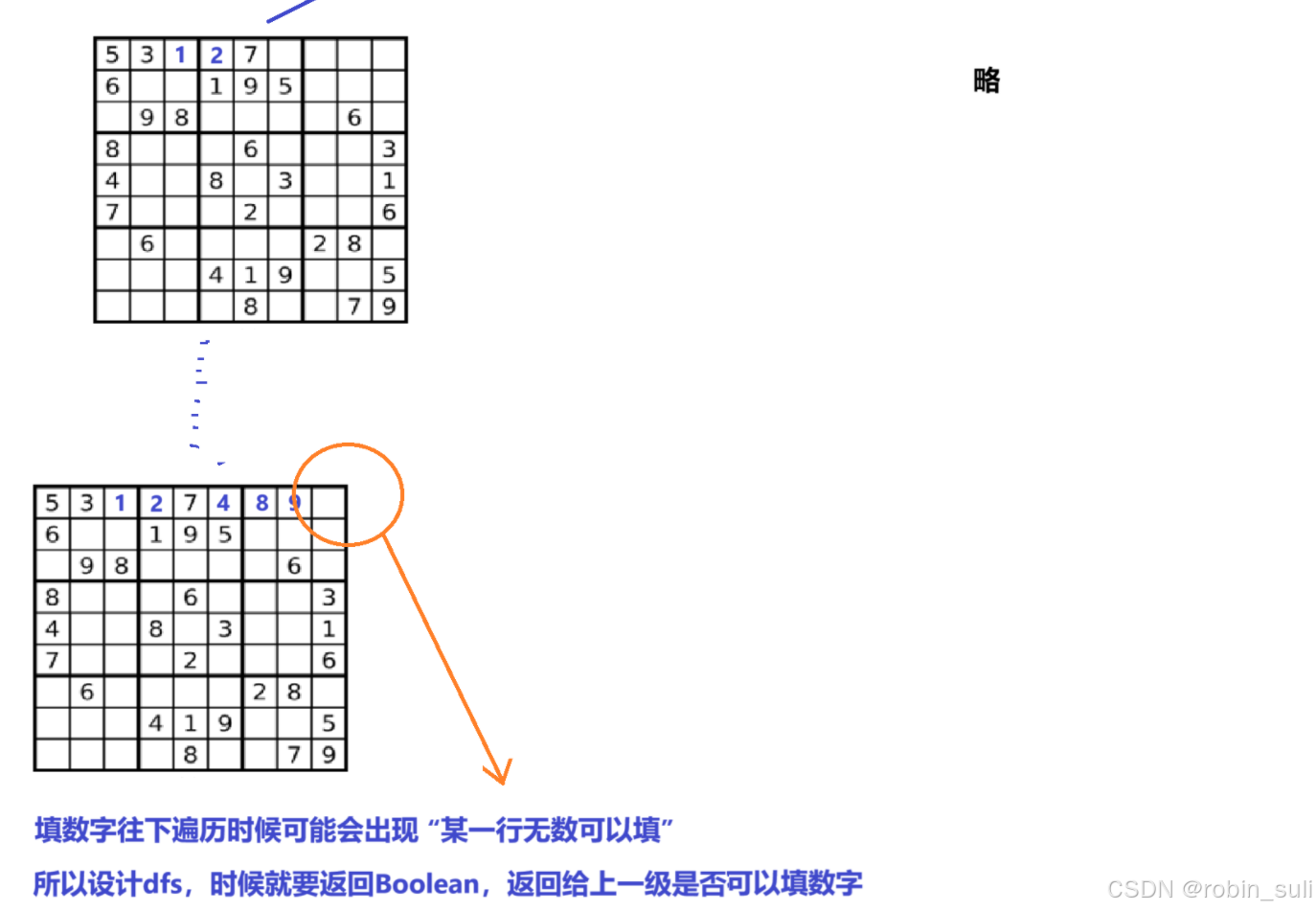
代码设计&剪枝&回溯： 

 

---

代码： 

class Solution {
    private boolean[][] row, col;
    private boolean[][][] gird; 

    public void solveSudoku(char[][] board) {
        //下标->数字；0->1, 1->2
        row = new boolean[9][10];
        col = new boolean[9][10];
        gird = new boolean[3][3][10];

        //初始化上面的标记数组
        for(int i = 0; i < 9; i++)
            for(int j = 0; j < 9; j++){
                int num = board[i][j]-'0';
                if(board[i][j] != '.'){
                    row[i][num] = col[j][num] = gird[i/3][j/3][num] = true;
                }
            }

        dfs(board);
    }

    private boolean dfs(char[][] board){
        for(int i = 0; i < 9; i++){
            for(int j = 0; j < 9; j++){
                if(board[i][j] == '.'){
                    for(int num = 1; num <= 9; num++){
                        //剪枝写法
                        if(!row[i][num] && !col[j][num] && !gird[i/3][j/3][num]){
                            board[i][j] = (char)('0' + num);
                            row[i][num] = col[j][num] = gird[i/3][j/3][num] = true;

                            //填数字往下遍历时候可能会出现 “某一行无数可以填”
                            if(dfs(board) == true) return true;

                            //回溯
                            board[i][j] = '.';
                            row[i][num] = col[j][num] = gird[i/3][j/3][num] = false;
                        }
                    }
                    //一整行都没有返回时(已经试过9个数)，也是出现“某一行无数可以填”
                    return false;
                }
            }
        }

        //上面没有返回代表，前面的dfs已经全部填完
        return true;
    }
}