[COCI2018-2019#3] Pismo
题目描述
给定一个包含 N N N 个整数的数组 A A A。
该数组中一个区间 [ L , R ] [L,R] [L,R] ( L < R L \lt R L<R)的值定义为 max ( A [ L ] , A [ L + 1 ] , ⋯ , A [ R ] ) − min ( A [ L ] , A [ L + 1 ] , ⋯ , A [ R ] ) \max(A[L],A[L+1],\cdots,A[R])-\min(A[L],A[L+1],\cdots,A[R]) max(A[L],A[L+1],⋯,A[R])−min(A[L],A[L+1],⋯,A[R])。
求该数组中所有区间值的最小值。
输入格式
第一行输入正整数 N N N。
第二行输入 N N N 个整数 A i A_i Ai,表示数组中的数。
输出格式
输出所有区间值的最小值。
样例 #1
样例输入 #1
2
1 3
样例输出 #1
2
样例 #2
样例输入 #2
3
1 1 1
样例输出 #2
0
样例 #3
样例输入 #3
5
1 2 1 2 1
样例输出 #3
1
提示
样例 3 解释
符合题意的区间为 [ 1 , 5 ] [1,5] [1,5],该区间的值为 max ( 1 , 2 , 1 , 2 , 1 ) − min ( 1 , 2 , 1 , 2 , 1 ) = 2 − 1 = 1 \max(1,2,1,2,1)-\min(1,2,1,2,1)=2-1=1 max(1,2,1,2,1)−min(1,2,1,2,1)=2−1=1,为所有区间中值最小的。
数据规模与规定
对于 20 20 20 分的数据, N ≤ 100 N \le 100 N≤100。
对于 40 40 40 分的数据, N ≤ 2000 N \le 2000 N≤2000。
对于 100 % 100\% 100% 的数据, 2 ≤ N ≤ 1 0 5 2 \le N \le 10^5 2≤N≤105, ∣ A i ∣ < 1 0 9 |A_i| \lt 10^9 ∣Ai∣<109。
说明
本题分值按 COCI 原题设置,满分 70 70 70。
题目译自 COCI2018-2019 CONTEST #3 T2 Pismo。
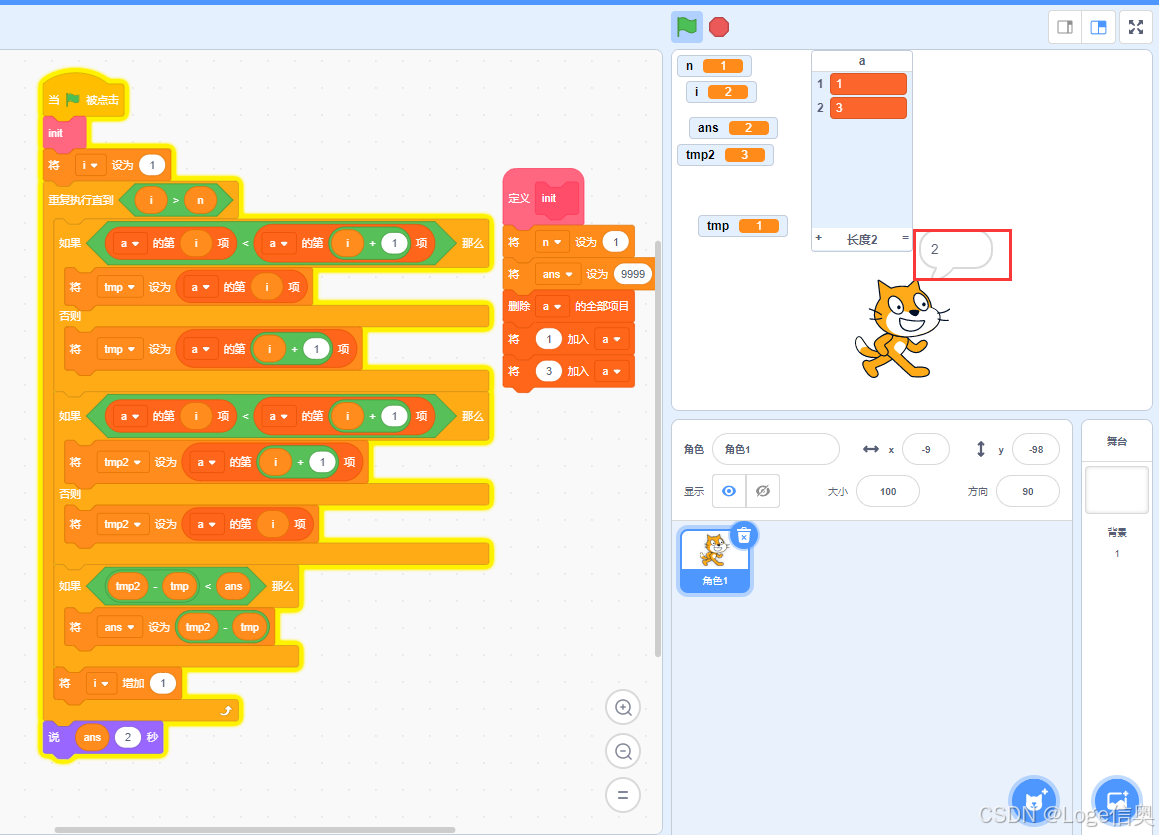
##Scratch实现
后续
接下来我会不断用scratch来实现信奥比赛中的算法题、Scratch考级编程题实现、白名单赛事考题实现,感兴趣的请关注,我后续将继续分享相关内容