算法编程题-颜色交替的最短路径

摘要：本文将对LeetCode原题 1129 颜色交替的最短路径进行介绍，先介绍dijkstra算法，然后给出进一步优化得到的bfs算法。代码实现基于golang语言，且已经通过所有测试用例，最后也会给出对应的时间复杂度分析。
关键词：LeetCode，Golang，dijkstra，bfs

原题描述

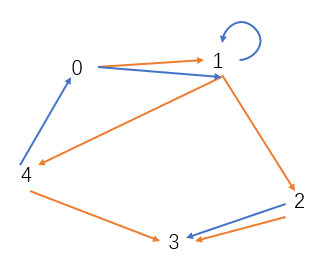
给定一个整数n，表示图中一共有n个节点，但是图中的边有红边也有蓝边，用两个数组给出red_edges和blue_edges，图中允许有自环和平行边，现在要求求出一个数组res[n]，res[i]表示从点0到点i的红色蓝色边交替出现的最短路径。如下图，是一个这样的有向图。
在这里插入图片描述

方法一、dijkstra算法

思路简述

稍微变型的单源最短路径问题，所以可以基于dijkstra算法来实现。在实现上，起始时，需要将起点0加入到堆中，并且要加入两次，对应两种颜色。加入到堆中的是一个状态，状态中的颜色表示到某点的一条路径的最后一段的颜色，起点前没有边，但是可以假想存在边，一种是红边，一种是蓝边。

代码实现

type LinkedListNode[T comparable] struct  {
	Val T
	Next *LinkedListNode[T]
}

type LinkedList[T comparable] struct {
	Head *LinkedListNode[T]
}

func (l *LinkedList[T]) InsertNode(v T) {
	curNode := &LinkedListNode[T]{Val: v}
	curNode.Next = l.Head
	l.Head = curNode
}


// NewLinkedList 根据数组新建一个链表
func NewLinkedList[T comparable] (arr []T) *LinkedList[T] {
	head := LinkedListNode[T]{Val: arr[0], Next: nil}
	tr := &head
	for i := 1; i < len(arr); i++ {
		tr.Next = &LinkedListNode[T]{Val: arr[i], Next: nil}
		tr = tr.Next
	}
	return &LinkedList[T]{Head: &head}
}


type AdjTableNode struct {
	Point int
}

type AdjTable struct {
	tab [][]*LinkedList[AdjTableNode]
}

func NewAdjTable(edges [][][]int, n int) *AdjTable {
	tab := make([][]*LinkedList[AdjTableNode], n)
	for i := 0; i < n; i++ {
		tab[i] = make([]*LinkedList[AdjTableNode], 2)
	}

	for i := 0; i < 2; i++ {
		for _, edge := range edges[i] {
			a, b := edge[0], edge[1]
			if tab[a][i] == nil {
				tab[a][i] = NewLinkedList[AdjTableNode]([]AdjTableNode{{Point: b}})
			} else {
				tab[a][i].InsertNode(AdjTableNode{b})
			}
		}
	}

	return &AdjTable{tab: tab}
}

type Point struct {
	PointNo int // 节点编号
	Dis     int // 节点距离
	Color   int // 上一条边蓝边0红边1
}

type Heap []*Point

func (h Heap) Len() int {
	return len(h)
}

func (h Heap) Less(i, j int) bool {
	return h[i].Dis < h[j].Dis
}

func (h Heap) Swap(i, j int) {
	h[i], h[j] = h[j], h[i]
}

func (h *Heap) Push(v interface{}) {
	*h = append(*h, v.(*Point))
}

func (h *Heap) Pop() interface{} {
	ret := (*h)[len(*h)-1]
	*h = (*h)[:len(*h)-1]
	return ret
}

func shortestAlternatingPaths(n int, redEdges [][]int, blueEdges [][]int) []int {
	edges := [][][]int{blueEdges, redEdges}
	adjTab := NewAdjTable(edges, n)
	dis := make([][]int, n)
	for i := 0; i < n; i++ {
		dis[i] = []int{-1, -1} // dis[i][0]表上上一条边为蓝色，dis[i][1]表示上一条边为红色
	}
	h := Heap{}
	// 初始化
	heap.Push(&h, &Point{0, 0, 0})
	heap.Push(&h, &Point{0, 0, 1})
	// 正式迭代
	// for i := 0; len(h) > 0 && i < 2 * n; i++ {
    for len(h) > 0 {
		p := heap.Pop(&h).(*Point)
		if dis[p.PointNo][p.Color] != -1 && dis[p.PointNo][p.Color] <= p.Dis {
			continue
		}

		dis[p.PointNo][p.Color] = p.Dis
		list := adjTab.tab[p.PointNo][1 ^ p.Color]
		if list == nil {
			continue
		}
		cur := list.Head
		for cur != nil {
			heap.Push(&h, &Point{cur.Val.Point, p.Dis + 1, 1 ^ p.Color})
			cur = cur.Next
		}
	}
	res := make([]int, n)
	for i := 0; i < n; i++ {
		res[i] = -1
		if dis[i][0] != -1 {
			res[i] = dis[i][0]
		}
		if dis[i][1] != -1 {
			if res[i] == -1 || res[i] > dis[i][1] {
				res[i] = dis[i][1]
			}
		}
	}
	return res
}

运行截图如下：
在这里插入图片描述

复杂度分析

时间复杂度： $O (n + m l o g m)$ ，其中n为点数，m为边数，在迭代循环中，考虑到堆中的数量级和边数有关
空间复杂度： $O (m + n)$

方法二、广度优先搜索

思路简述

还有一种可行的思路不能忘记，考虑到图中每一条边的权重都是1，所以也可以使用广度优先搜索的方法去做。每一个节点第一次被访问到此时的路径长度就是其到源点0的最短路径。

代码实现

type LinkedListNode[T comparable] struct  {
	Val T
	Next *LinkedListNode[T]
}

type LinkedList[T comparable] struct {
	Head *LinkedListNode[T]
}

func (l *LinkedList[T]) InsertNode(v T) {
	curNode := &LinkedListNode[T]{Val: v}
	curNode.Next = l.Head
	l.Head = curNode
}


// NewLinkedList 根据数组新建一个链表
func NewLinkedList[T comparable] (arr []T) *LinkedList[T] {
	head := LinkedListNode[T]{Val: arr[0], Next: nil}
	tr := &head
	for i := 1; i < len(arr); i++ {
		tr.Next = &LinkedListNode[T]{Val: arr[i], Next: nil}
		tr = tr.Next
	}
	return &LinkedList[T]{Head: &head}
}


type AdjTableNode struct {
	Point int
}

type AdjTable struct {
	tab [][]*LinkedList[AdjTableNode]
}

func NewAdjTable(edges [][][]int, n int) *AdjTable {
	tab := make([][]*LinkedList[AdjTableNode], n)
	for i := 0; i < n; i++ {
		tab[i] = make([]*LinkedList[AdjTableNode], 2)
	}

	for i := 0; i < 2; i++ {
		for _, edge := range edges[i] {
			a, b := edge[0], edge[1]
			if tab[a][i] == nil {
				tab[a][i] = NewLinkedList[AdjTableNode]([]AdjTableNode{{Point: b}})
			} else {
				tab[a][i].InsertNode(AdjTableNode{b})
			}
		}
	}

	return &AdjTable{tab: tab}
}

type Point struct {
	PointNo int // 节点编号
	Dis     int // 节点距离
	Color   int // 上一条边蓝边0红边1
}

type Heap []*Point

func (h Heap) Len() int {
	return len(h)
}

func (h Heap) Less(i, j int) bool {
	return h[i].Dis < h[j].Dis
}

func (h Heap) Swap(i, j int) {
	h[i], h[j] = h[j], h[i]
}

func (h *Heap) Push(v interface{}) {
	*h = append(*h, v.(*Point))
}

func (h *Heap) Pop() interface{} {
	ret := (*h)[len(*h)-1]
	*h = (*h)[:len(*h)-1]
	return ret
}

func shortestAlternatingPaths(n int, redEdges [][]int, blueEdges [][]int) []int {
edges := [][][]int{blueEdges, redEdges}
	adjTab := NewAdjTable(edges, n)
	dis := make([][]int, n)
	for i := 0; i < n; i++ {
		dis[i] = []int{-1, -1}
	}
	oldqueue := []*Point{{0, 0, 0}, {0, 0, 1}}
	queue := make([]*Point, 0)
	for len(oldqueue) > 0  {
		for _, p := range oldqueue {
			if dis[p.PointNo][p.Color] == -1 {
				dis[p.PointNo][p.Color] = p.Dis
			} else {
				continue
			}
			list := adjTab.tab[p.PointNo][1 ^ p.Color]
			if list == nil {
				continue
			}
			cur := list.Head
			for cur != nil {
				queue = append(queue, &Point{cur.Val.Point, p.Dis + 1, 1 ^ p.Color})
				cur = cur.Next
			}
		}
		oldqueue = queue
		queue = []*Point(nil)
	}

    res := make([]int, n)
	for i := 0; i < n; i++ {
		res[i] = -1
		if dis[i][0] != -1 {
			res[i] = dis[i][0]
		}
		if dis[i][1] != -1 {
			if res[i] == -1 || res[i] > dis[i][1] {
				res[i] = dis[i][1]
			}
		}
	}
	return res
}

运行截图如下：
在这里插入图片描述

复杂度分析

时间复杂度： $O (m + n)$ ，m为边数，n为点数
空间复杂度： $O (m + n)$

参考

颜色交替的最短路径