引:
2023年C题第二问,让我们探索成本和销售量之间的关系,可以利用回归来分析。
目录
一、回归:
1.1回归分析定义:
通过研究X和Y的相关关系,尝试去解释Y的形成机制,进而达到通过X去预测Y的目的。
回归研究的是相关关系,是相关性,不是因果性!
X是自变量,Y是因变量;X为解释变量,Y为被解释变量
1.2回归分析要完成的三个使命:
第一、识别重要变量; 第二、判断相关性的方向; 第三、要估计权重(回归系数)
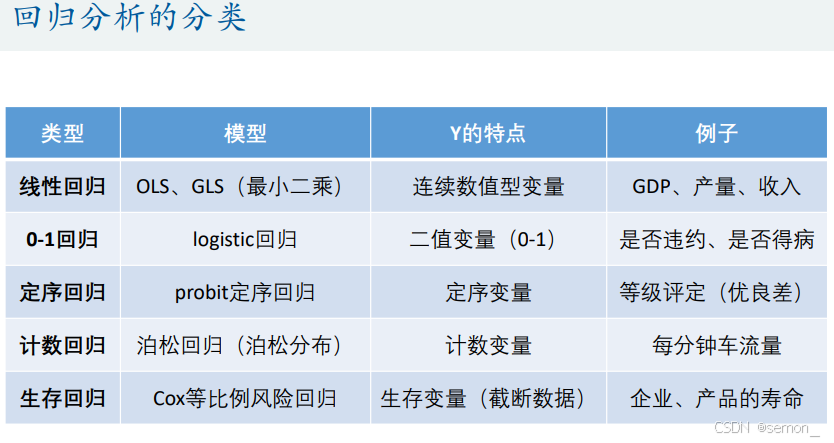
1.3回归分类:
按照Y的特点可以分为:
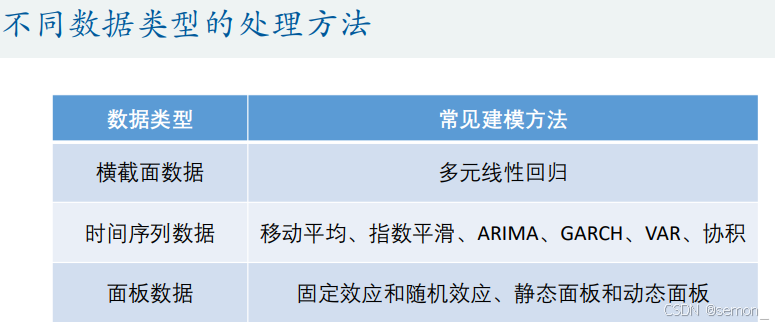
按照数据类型可以分为:
本篇文章讨论的是:
Y为连续性数值变量且数据类型为横截面数据所采用的建模方法——多元线性回归
二、线性回归
一元线性回归——拟合法的原理,见:填补缺失数据:插值法、拟合法_补数据的方法拟合法-CSDN博客
2.1理解线性:
如果是下面这种情况,可以通过EXCEL进行变量替换,变成严格的线性关系。
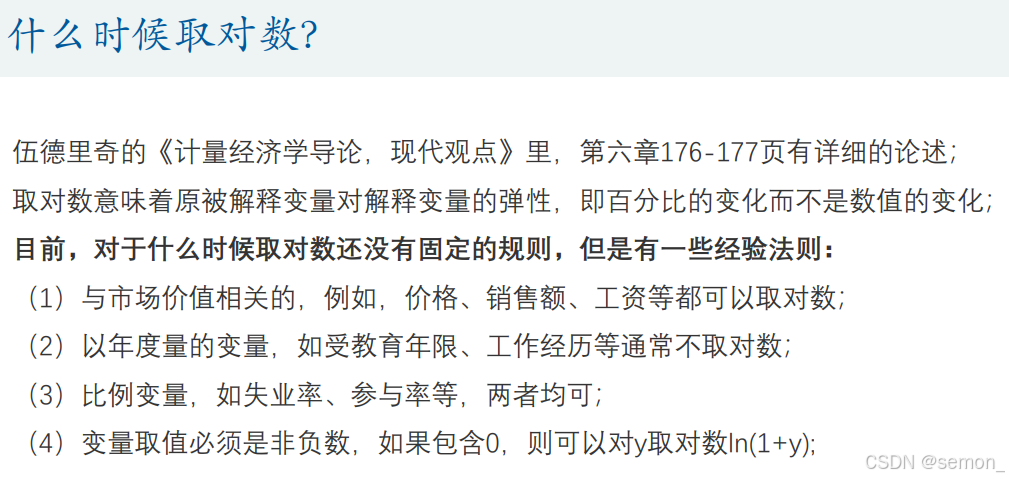
那么我们什么时候会选取对数这样的形式呢?
2.2解决内生性问题:
无内生性要求所有解释变量均与扰动项不相关。 这个假定通常太强,因为解释变量一般很多(比如,5‐15个解释变量), 且需要保证它们全部外生。
是否可能弱化此条件?
答案是肯定的,如果你的解释变量可以区分为核心解释变量(我们感兴趣的变量)与控制变量两类(从干扰项中剥离出来的和解释变量相关的变量)
这样可以保证核心解释变量与扰动项不相关。
2.3回归系数的解释:
回归系数的解释,便是在解释相关关系!
2.4定性变量的处理:
用虚拟变量替换,如下:
2.5标准化回归系数:
遇到R方过小,怎么办?
(1)回归分为解释型回归和预测型回归。 预测型回归一般才会更看重。
解释型回归更多的关注模型整体显著性以及自变量的统计显著性和经济意义显著性即可。
(2)可以对模型进行调整,例如对数据取对数或者平方后再进行回归。
(3)数据中可能有存在异常值或者数据的分布极度不均匀。
三、Stata软件实操
3.1处理虚拟变量:
tabulate 变量名,gen(A)
返回对应的这个变量的频率分布表,并生成对应的虚拟变量(以A开头)。
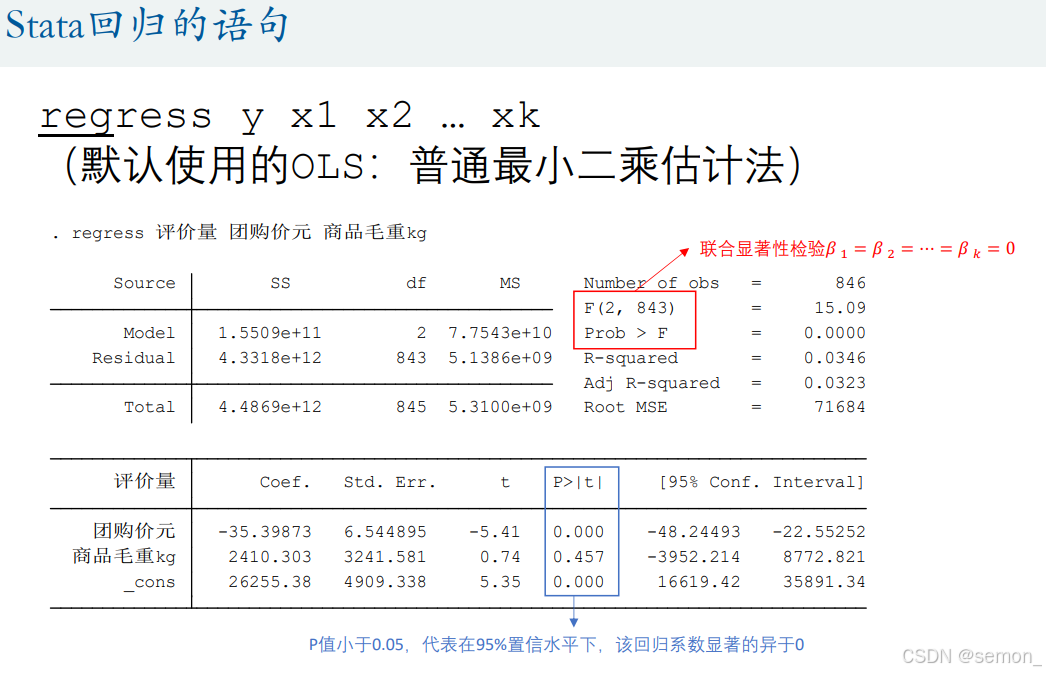
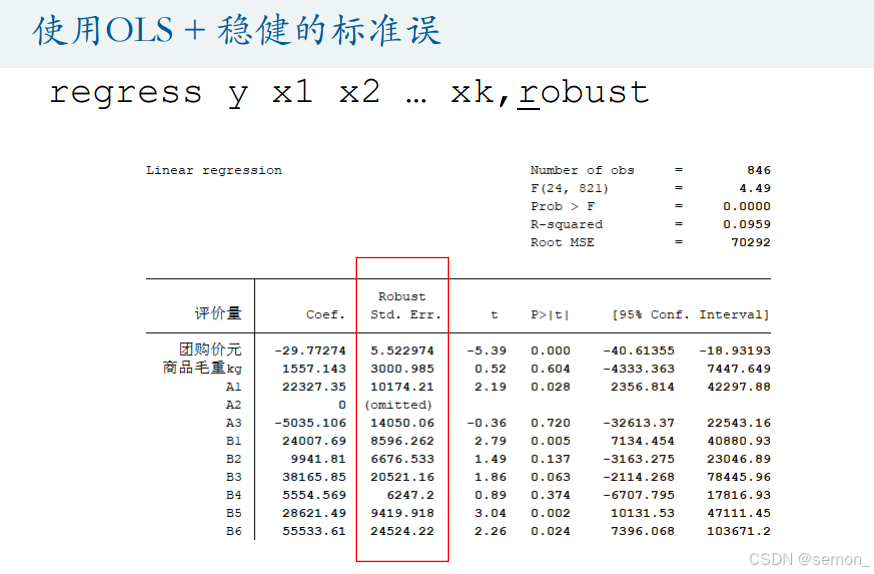
3.2回归语句:
3.3标准化回归系数
消除量纲影响,只需要在语句末尾+b
根据系数大小,便可以判断出影响y的重要因素。
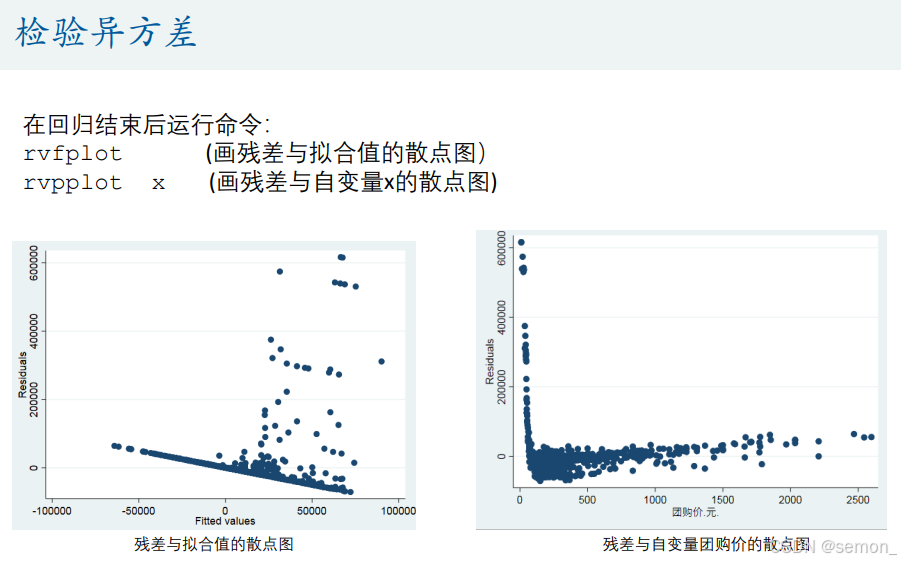
3.3异方差处理:
如果发现存在异方差,使用OLS + 稳健的标准误 。
3.4多重共线性处理:
导致F,t检验显著性不高(预测不用管,解释要管)
F原假设为:,所以必须要拒绝原假设。
小于0.05代表在置信水平为95%拒绝原假设。
解决办法:逐步回归法