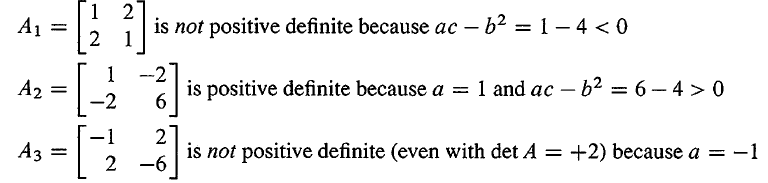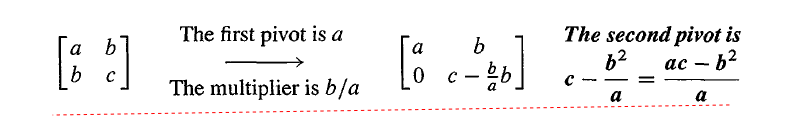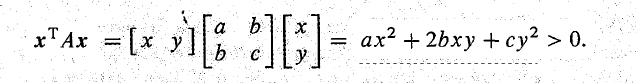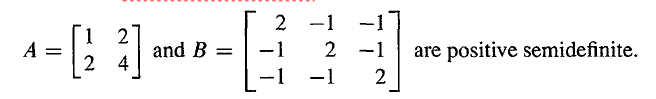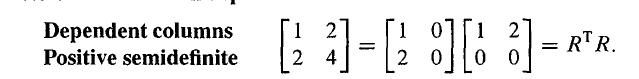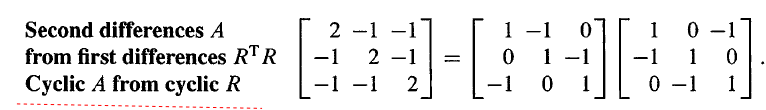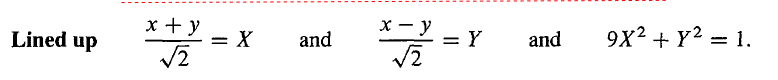这部分我们关注有正特征值的对称矩阵。如果对称性使得一个矩阵重要，那么所有特征值大于零这个额外属性则让这个矩阵真正特殊。但我们这里的特殊并不是稀少，事实上在各种应用中具有正特征值的对称矩阵非常常见，它们被称作正定矩阵。

我们可以通过检查特征值是否大于零来识别正定矩阵，但计算特征值是一项工作，当我们真正需要它们的时候我们可以进行计算，而如果我们仅仅想知道它们是否是正的，我们有更快的方式。

1. 正定矩阵的判断

首先，由于矩阵是对称的，所有的特征值自然都是实数。让我们以一个 2×2 的矩阵开始，

$$A=\left[\begin{array}{cc}a& b\\ b& c\end{array}\right]$$

A 的特征值是正的当且仅当 $a>0$ 并且 $ac-b^2>0$。

如果 2×2 矩阵的特征值 ${\lambda }_1>0$，${\lambda }_2>0$，那么它们的乘积等于行列式， ${\lambda }_1{\lambda }_2=|A|=ac-b^2>0$，它们的和等于矩阵的迹，${\lambda }_1+{\lambda }_2=a+c>0$，所以 $a$ 和 $c$都必须是正的。

A 的特征值是正的当且仅当主元是正的。

这连接了线性代数的两大部分，正的特征值意味着正的主元，反之亦然。而且，主元往往比特征值计算得更快。

• 基于能量的定义

$$Ax=\lambda x\to x^{T}Ax=\lambda x^{T}x=\lambda ||x|{|}^2>0$$

所以，如果特征值大于零，$x^{T}Ax$ 对于所有的特征向量也大于零。事实上，不仅仅是特征向量，针对任意非零向量 $x$，上式也同样成立。

A 是正定的，如果有 $x^{T}Ax>0$ 对任意非零向量都成立。

从这个定义中我们可以得出，如果 $A,B$ 是对称的正定矩阵，那么 $A+B$ 也是.

如果 $R$ 的列是不相关的，那么 $A=R^{T}R$ 是正定的。

$$x^{T}Ax=x^T{R}^{T}Rx=(Rx{)}^{T}Rx=||Rx|{|}^2$$

因为 $R$ 的列是不相关的，所以针对任意非零向量 $x$，$Rx\ne 0$。

当一个对称的矩阵具有下列五个属性之一，那么它一定满足所有的属性。

• 1. 所有的 $n$ 个主元是正的。
• 2. 所有的 $n$ 个左上行列式是正的，也就是 $1\times 1,2\times 2\cdots n\times n$ 的行列式。
• 3. 所有的 $n$ 个特征值是正的。
• 4. $x^{T}Ax>0$ 除了零向量。
• 5. $A=R^{T}R$ 对于一个有着不相关列的矩阵 $R$。

2. 半正定矩阵

经常情况我们会在正定的边缘，行列式为零，最小的特征值为零，这些在边缘的矩阵被称为半正定矩阵。

$A$ 的特征值为 5 和 0，左上行列式为 1 和 0，它的秩为 1，可以被分解为具有相关列的矩阵 $R^{T}R$。

如果将元素 4 增加一个任意小的数字，那么矩阵将会变成正定的。同样地， $B$ 也可以写成 $R^{T}R$ 的形式，但是 $R$ 的列肯定是相关的。

3. 第一个应用：椭圆 $a{x}^2+2bxy+c{y}^2=1$

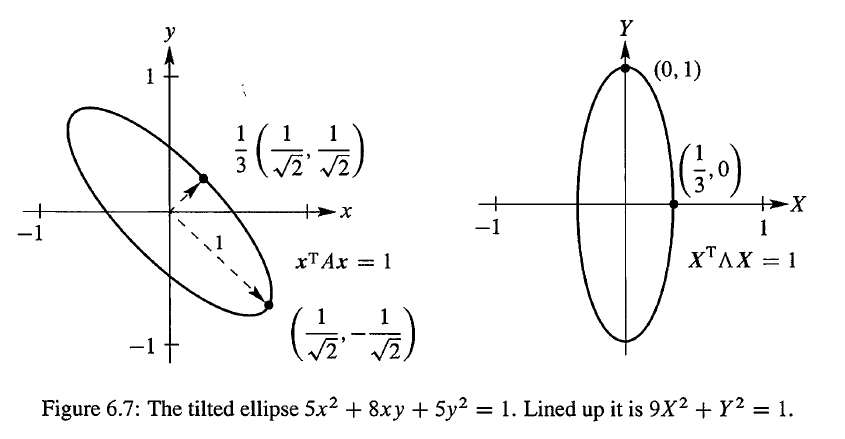
1. 倾斜的椭圆和矩阵 A 联系在一起，$x^{T}Ax=1$。
2. 排好的椭圆和矩阵 $\Lambda$ 联系在一起，$X^T\Lambda X=1$。
3. 将椭圆排好的旋转矩阵则是特征向量矩阵 $Q$。

针对椭圆方程 $5x^2+8xy+5y^2=1$，我们有：

$$\left[\begin{array}{cc}x& y\end{array}\right]\left[\begin{array}{cc}5& 4\\ 4& 5\end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right]=1A=\left[\begin{array}{cc}5& 4\\ 4& 5\end{array}\right]$$

将 $A$ 分解为 $Q\Lambda Q^T$ 我们得到：

$$\left[\begin{array}{cc}5& 4\\ 4& 5\end{array}\right]=\frac{1}{\sqrt{2}}\left[\begin{array}{cc}1& 1\\ 1& -1\end{array}\right]\left[\begin{array}{cc}9& 0\\ 0& 1\end{array}\right]\frac{1}{\sqrt{2}}\left[\begin{array}{cc}1& 1\\ 1& -1\end{array}\right]$$

椭圆方程则也可以重写为：

$$5x^2+8xy+5y^2=1=9\ast (\frac{x+y}{\sqrt{2}}{)}^2+1\ast (\frac{x-y}{\sqrt{2}}{)}^2$$

可以看到，方程的系数是两个特征值 9 和 0，而在平方内部则是两个特征向量 $(1,1)/\sqrt{2}$ 和 $(1,-1)/\sqrt{2}$。椭圆的坐标轴是沿着特征向量的方向，这也就是为什么 $A=Q\Lambda Q^T$ 被称作主轴定理，特征向量指出了坐标轴的方向，特征值则指出了长度。

将椭圆排好后，较大的特征值 9 给出了短半轴的长度 $1/{\sqrt{\lambda }}_1=1/3$，较小的特征值 1 给出了长半轴的长度 $1/{\sqrt{\lambda }}_2=1$。在 $xy$ 系统中，坐标轴沿着 $A$ 的特征向量的方向，而在 $XY$ 系统中，坐标轴沿着 $\Lambda$ 的特征向量的方向。

获取更多精彩，请关注「seniusen」!