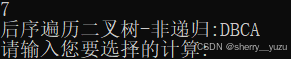目录
实验内容
1.编写函数,输入字符序列,建立二叉树的二叉链表。
2.编写函数,实现二叉树的中序递归遍历算法。(最好也能实现前缀和后缀遍历算法)
3.编写函数,实现二叉树的中序非递归遍历算法。
4.编写函数,借助队列实现二叉树的层次遍历算法。
5.编写函数,求二叉树的高度。
6.编写函数,求二叉树的结点个数。
7.编写函数,求二叉树的叶子个数。
8.编写函数,交换二叉树每个结点的左子树和右子树。
9.编写一个主函数,在主函数中设计一个简单的菜单,分别调试上述算法。
源码
#include <iostream>
#include <string>
#include <stack>
using namespace std;
#define ElemType char // 二叉链表结点类型
#define MAX_SIZE 128
// 定义树
typedef struct BiTNode {
ElemType data;
struct BiTNode* lchild, * rchild;
}BiTNode, * BiTree;
// 建立二叉链表
void createNode(BiTree& T)
{
ElemType e;
cin >> e;
if (e == '#') {
T = NULL;
}
else {
T = (BiTree)malloc(sizeof(BiTNode));
T->data = e;
createNode(T->lchild);
createNode(T->rchild);
}
}
// 打印节点中的数据
void printNodeData(BiTree Node) {
cout << Node->data;
}
// 递归法遍历
// 1. 前序
void preOrder(BiTree root) {
if (root != NULL) {
printNodeData(root); // 打印根
preOrder(root->lchild); // 递归左子树
preOrder(root->rchild); // 递归右子树
}
}
// 2. 中序
void midOrder(BiTree root) {
if (root != NULL) {
midOrder(root->lchild); // 递归左子树
printNodeData(root); // 打印根
midOrder(root->rchild); // 递归右子树
}
}
// 3. 后序
void lastOrder(BiTree root) {
if (root != NULL) {
lastOrder(root->lchild); // 递归左子树
lastOrder(root->rchild); // 递归右子树
printNodeData(root); // 打印根
}
}
// 非递归法
// 1. 前序
void preOrderByStack(BiTree root) {
if (root == NULL) {
return;
}
// 定义栈
BiTree stack[10]; // 存储每次打印节点的位置
int stackTop = -1; // 栈顶标记
BiTree pMove = root; // 移动指针代表当前节点 从root开始
while (stackTop != -1 || pMove != NULL) { // 栈不为空或当前节点不为空
// 从根开始找到最左边
while (pMove) { // 如果当前节点不为空
printNodeData(pMove); // 打印当前节点
stackTop++;
stack[stackTop] = pMove; // 走过的节点入栈
pMove = pMove->lchild; // 当前指针变为左子节点 继续上述操作
}
// 上面的左边操作找完 找右边
if (stackTop != -1) {
pMove = stack[stackTop]; // 获取栈顶元素
stackTop--; // 栈顶元素出栈
pMove = pMove->rchild; // 当前指针变为右子节点 继续上述操作
}
}
}
// 2. 中序
void midOrderByStack(BiTree root) {
if (root == NULL) {
return;
}
BiTree stack[10];
int stackTop = -1;
BiTree pMove = root;
while (stackTop != -1 || pMove != NULL) {
// 找到最左边
while (pMove) {
stackTop++;
stack[stackTop] = pMove;
pMove = pMove->lchild;
}
// 左边找完
if (stackTop != -1) {
pMove = stack[stackTop];
stackTop--;
printNodeData(pMove);
pMove = pMove->rchild;
}
}
}
// 3. 后序
void lastOrderByStack(BiTree root) {
if (root == NULL) {
return;
}
BiTree stack[10];
int stackTop = -1;
BiTree pMove = root;
BiTree isVist = NULL; // 判断是否被访问过的标志
// 找到最左边
while (pMove) {
stackTop++;
stack[stackTop] = pMove;
pMove = pMove->lchild;
}
// 回退 遇到根先判断根的左右是否被访问过或为空
while (stackTop != -1) {
pMove = stack[stackTop];
stackTop--;
// 已经走到最左边 所以不可能再有左边 只用判断右边
// 右节点为空或已经被访问
if (pMove->rchild == NULL || pMove->rchild == isVist) {
printNodeData(pMove); // 打印当前节点
isVist = pMove; // 改变标志位置
}
else { //右节点没被访问过
stackTop++;
stack[stackTop] = pMove; // 回退的当前节点的根节点
pMove = pMove->rchild; // 找到根节点的右节点
while (pMove) { // 重复找到最左边的操作
stack[++stackTop] = pMove;
pMove = pMove->lchild;
}
}
}
}
// 定义顺序队
typedef struct Quene {
int front; // 队头指针
int rear; // 队尾指针
BiTree data[MAX_SIZE]; // 存放队中元素
}SqQueue;
// 初始化队列
void initQueue(SqQueue** q) {
if (!((*q) = (SqQueue*)malloc(sizeof(SqQueue)))) {
cout << ("内存分配失败!");
exit(-1);
}
(*q)->front = (*q)->rear = -1; // 置 -1
}
// 判断队列是否为空
bool emptyQueue(SqQueue* q) {
// 首指针和尾指针相等 为空 返回真
if (q->front == q->rear) {
return true;
}
// 不为空 返回假
return false;
}
// 进队列
bool enQueue(SqQueue* q, BiTree node) {
// 队列满了 插入失败 返回假,
if (q->rear == MAX_SIZE - 1) {
return false;
}
// 队列没满 插入成功 返回真
q->rear++; // 头指针加 1
q->data[q->rear] = node; // 传值
return true;
}
// 出队列
bool deQueue(SqQueue* q, BiTree* node) {
// 队列为空 取出失败 返回假
if (q->front == q->rear) {
return false;
}
// 队列不为空 取出成功 返回真
q->front++; // 尾指针+ 1
*node = q->data[q->front]; // 取值
return true;
}
// 层次遍历
void levelOrder(BiTree T) {
SqQueue* q; // 定义队列
initQueue(&q); // 初始化队列
if (T != NULL) { // 根节点指针进队列
enQueue(q, T);
}
// 一层一层的把节点存入队列,当没有孩子节点时就不再循环
while (!emptyQueue(q)) { // 队不为空
deQueue(q, &T); // 出队时的节点
cout << (T->data); // 输出节点存储的值
if (T->lchild != NULL) { // 有左孩子时将该节点进队列
enQueue(q, T->lchild);
}
if (T->rchild != NULL) { // 有右孩子时将该节点进队列
enQueue(q, T->rchild);
}
}
}
// 求二叉树的高度
int treeHeight(BiTree T)
{
int hL, hR, Height;
if (T == NULL)
{ // 空树 高度为0
return 0;
}
else
{
hL = treeHeight(T->lchild); // 求左子树的高度
hR = treeHeight(T->rchild); // 求右子树的高度
Height = ((hL > hR) ? hL : hR) + 1; // 取高度较大者 加上根结点的高度
return Height;
}
}
// 求二叉树的结点数
int nodeCount(BiTree T)
{
static int count = 0; // 叶子数
if (T == NULL) { // 空树
return (0);
}
else if (T->lchild != NULL || T->rchild != NULL) { // 有左孩子或有右孩子
count++;
}
nodeCount(T->lchild);
nodeCount(T->rchild);
return count;
}
// 求二叉树的叶子数
int leafcount(BiTree T)
{
static int count = 0; // 叶子数
if (T == NULL) { // 空树
return (0);
}
else if (T->lchild == NULL && T->rchild == NULL) { // 无左孩子且无右孩子
count++;
}
leafcount(T->lchild);
leafcount(T->rchild);
return count;
}
// 交换左右子树
void swap(BiTree T) {
BiTree temp = 0;
if (T != NULL) {
temp = T->lchild;
T->lchild = T->rchild;
T->rchild = temp;
swap(T->lchild);
swap(T->rchild);
}
}
int main() {
BiTree T = 0;
int num;
cout << "1. 输入字符序列,建立二叉链表" << endl;
cout << "2. 先序遍历二叉树:递归算法" << endl;
cout << "3. 先序遍历二叉树:非递归算法" << endl;
cout << "4. 中序遍历二叉树:递归算法" << endl;
cout << "5. 中序遍历二叉树:非递归算法" << endl;
cout << "6. 后序遍历二叉树:递归算法" << endl;
cout << "7. 后序遍历二叉树:非递归算法" << endl;
cout << "8. 借助队列实现二叉树的层次遍历" << endl;
cout << "9. 求二叉树的高度" << endl;
cout << "10. 求二叉树的结点数" << endl;
cout << "11. 求二叉树的叶子数" << endl;
cout << "12. 交换二叉树每个结点的左子树和右子树" << endl;
cout << "13. 退出";
cout << endl;
while (true)
{
cout << "请输入您要选择的计算: " << endl;
cin >> num;
switch (num)
{
case 1: //调用递归建立二叉树算法
{
cout << "请输入二叉树各结点值, 例如:AB#D##C##" << endl;
createNode(T);
cout << endl;
}break;
case 2:
{
cout << "先序遍历二叉树-递归:";
preOrder(T);
cout << endl;
}break;
case 3:
{
cout << "先序遍历二叉树-非递归:";
preOrderByStack(T);
cout << endl;
}break;
case 4:
{
cout << "中序遍历二叉树-递归:";
midOrder(T);
cout << endl;
}break;
case 5:
{
cout << "中序遍历二叉树-非递归:";
midOrderByStack(T);
cout << endl;
}break;
case 6:
{
cout << "后序遍历二叉树-递归:";
lastOrderByStack(T);
cout << endl;
}break;
case 7:
{
cout << "后序遍历二叉树-非递归:";
lastOrderByStack(T);
cout << endl;
}break;
case 8:
{
cout << "层次遍历二叉树:";
levelOrder(T);
cout << endl;
}break;
case 9:
{
cout << "二叉树的高度为:";
cout << treeHeight(T);
cout << endl;
}break;
case 10:
{
cout << "二叉树的结点数为:";
cout << nodeCount(T);
cout << endl;
}break;
case 11:
{
cout << "二叉树的叶子数为:";
cout << leafcount(T);
cout << endl;
}break;
case 12:
{
cout << "交换二叉树每个结点的左子树和右子树:" << endl;
swap(T);
cout << "交换成功!您可继续输入选择查看交换后的遍历结果" << endl;
}break;
case 13:
{
cout << "退出成功!" << endl;
system("pause");
return 0;
}break;
default:
{
cout << "输入错误!请重新输入!" << endl;
}
}
}
system("pause");
return 0;
}一、实验目的
掌握二叉树的基础知识,掌握二叉树的链表存储,遍历的递归与非递归算法,层次遍历、计算结点数、叶子数等二叉树有关算法的代码实现。理解递归算法的执行步骤,学会字符类型数据在输入时的处理,理解如何利用栈结构实现非递归算法。
二、问题分析及数据结构设计
- 问题分析:需要输入字符序列,建立二叉树的二叉链表。实现二叉树的中序递归及非递归遍历算法。借助队列实现二叉树的层次遍历算法。求二叉树的高度、结点个数、叶子个数。交换二叉树每个结点的左子树和右子树。需要我们思考如何用字符序列来表示一棵树,理解二叉树遍历的递归及非递归思想,判断是叶子还是结点,如有孩子的是结点,左右都无孩子的就是叶子。需要我们知道队列的相关知识,实现用队列的方法进行层次遍历。
- 数据结构设计:二叉链表结点类型-char字符型。树的定义:树-BiTNode,数据data-char字符型,左子树-指针BiTNode * lchild,右子树-指针BiTNode * rchild。队列的定义:队列-Quene,头指针front-int整型,尾指针rear-int整型。树的高度Hight-int整型,左子树的高度hL-int整型,右子树的高度hR-int整型。叶子数count-int整型,结点数count-int整型。用户输入选择要进行的算法序号num-int整型。
三、算法设计(伪代码表示)
1. 输入字符序列 创建二叉链表
Function createNode(BiTree & T)
Begin
输入字符
IF 字符 = ’#’
树为空
ELSE
分配BiTree大小的内存空间给T
T->data = e
递归createNode(T的左子树)
递归createNode(T的右子树)
End
2. 递归前序遍历
Function preOrder(BiTree root)
Begin
IF 树的根!=空
打印根的data
递归preOrder(根的左子树)
递归preOrder(根的右子树)
End
3. 递归中序遍历
Function midOrder(BiTree root)
Begin
IF 树的根!=空
递归midOrder(根的左子树)
打印根的data
递归midOrder(根的右子树)
End
4. 递归后序遍历
Function lastOrder(BiTree root)
Begin
IF 树的根!=空
递归preOrder(根的左子树)
递归preOrder(根的右子树)
打印根的data
End
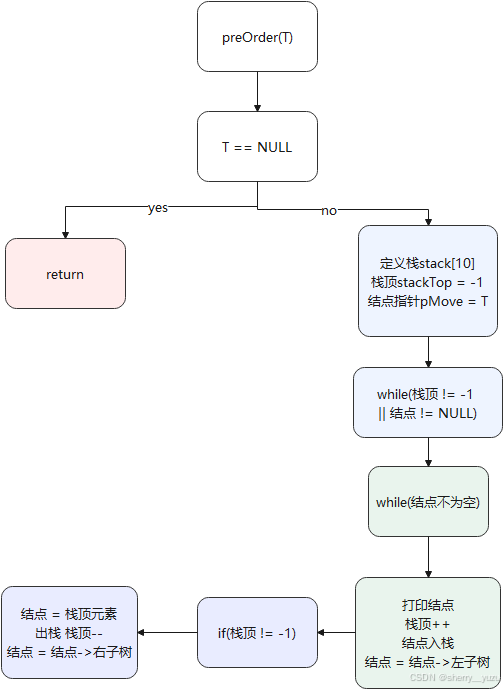
5. 非递归前序遍历
Function lastOrderByStack(BiTree root)
Begin
IF 树的根==空
retutn
ELSE
定义栈stack
栈顶标记stackTop = -1
移动指针pMove = 树的根
WHILE 树根 != NULL || 栈顶 != -1
WHILE 树根 != NULL
打印当前结点pMove
栈顶标志++
pMove结点入栈
结点 = 结点->左子树
IF 栈顶 != -1
pMove = 栈顶
栈顶标志--
结点 = 结点->右子树
End
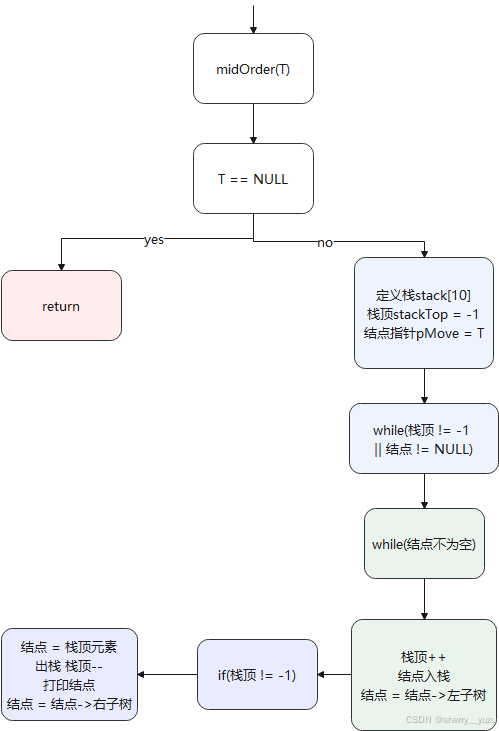
6. 非递归中序遍历
Function midOrderByStack(BiTree root)
Begin
IF 根 == NULL
return
建立栈stack
初始化结点指针pMove = 根root
WHILE 结点 != NULL || 栈顶 != -1
WHILE 结点 != NULL
栈顶标志++
结点入栈
结点 = 结点->左子树
IF 栈顶 != -1
结点 = 栈顶元素
栈顶标志--
打印结点
结点 = 结点->右子树
End
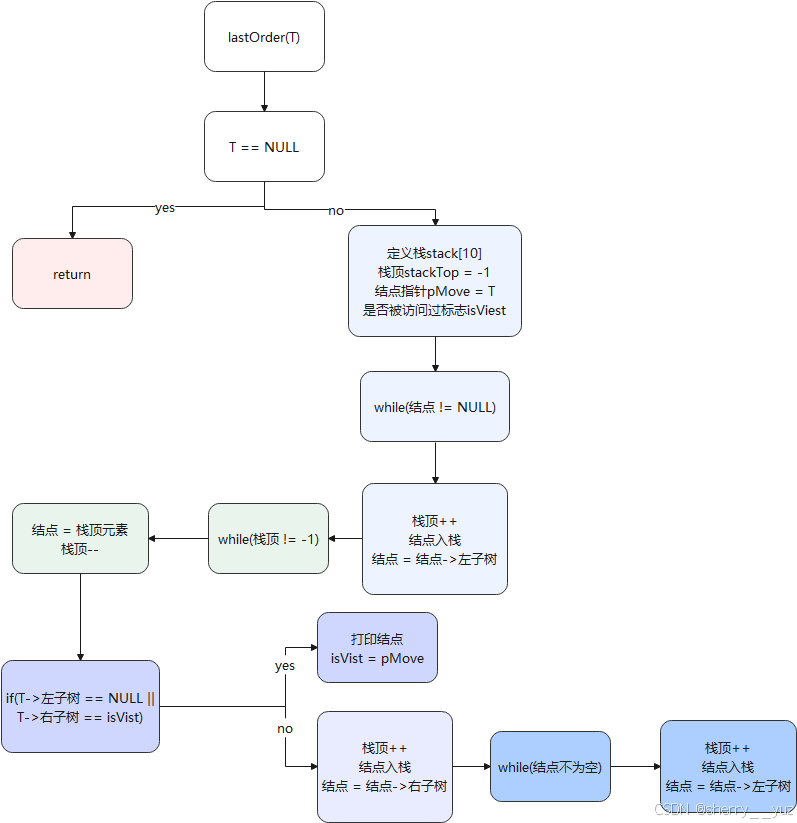
7. 非递归后序遍历
Function lastOrderByStack(BiTree root)
Begin
IF 根 == NULL
return
建立栈stack
初始化结点指针pMove = 根root
WHILE 结点 != NULL
栈顶标志++
结点入栈
结点 = 结点->左子树
WHILE 栈顶 != -1
结点 = 栈顶元素
栈顶标志--
IF 结点->左子树 == NULL || 结点->右子树 被访问过
打印结点
标记结点被访问
ELSE
栈顶标志++
栈顶 = 根结点
结点 = 结点->右子树
WHILE 结点 != NULL
栈顶标志++
结点入栈
结点 = 结点->左子树
End
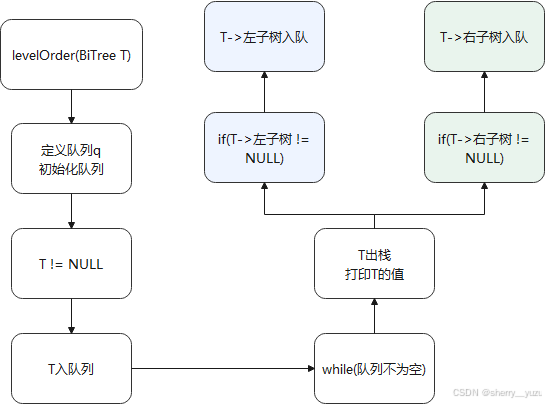
8. 层次遍历
Function levelOrder(BiTree T)
Begin
定义队列q
初始化队列
IF 根!=NULL
结点入队列
WHILE 队!=NULL
节点出队
cout结点->data
IF 节点->左子树!=NULL
节点->左子树入队
IF 节点->右子树!=NULL
节点->右子树入队
End
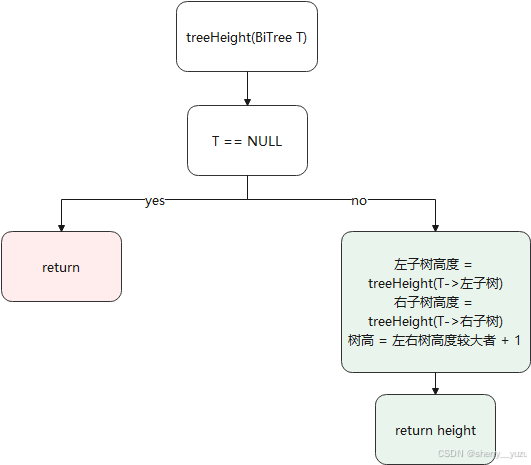
9. 求二叉树的高度
Function int treeHeight(BiTree T)
Begin
IF 树根 == NULL
retutn 0
ELSE
左子树高度 = treeHeight(结点->左子树)
右子树高度 = treeHeight(结点->左右子树)
IF 左子树高度 > 右子树高度
return 左子树高度 + 1
ELSE
return 右子树高度 + 1
End
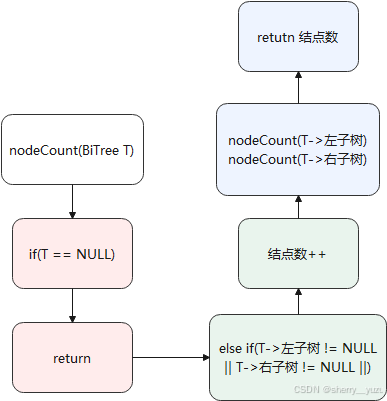
10. 求二叉树的结点数
Function int nodeCount(BiTree T)
Begin
IF 树根 == NULL
return 0
ELSE IF 结点->左子树 != NULL || 结点->右子树 != NULL
结点数++
nodeCount(结点->左子树)
nodeCount(结点->右子树)
return 结点数
End
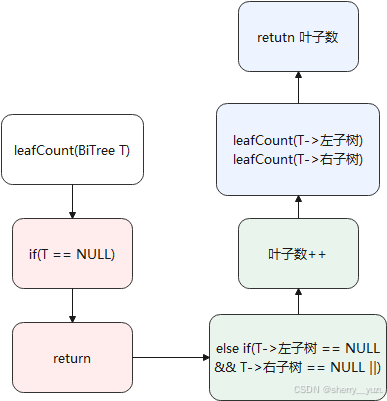
11. 求二叉树的叶子数
Function int leafCount(BiTree T)
Begin
IF 树根 == NULL
return 0
ELSE IF 结点->左子树 == NULL && 结点->右子树 == NULL
结点数++
leafCount(结点->左子树)
leafCount(结点->右子树)
return 叶子数
End
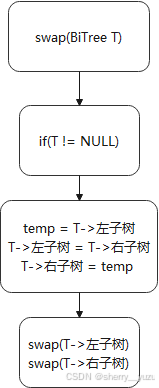
12. 交换左右子树
Function swap(BiTree T)
Begin
IF 树根 != NULL
temp = 结点->左子树
结点->左子树 = 结点->右子树
结点->右子树 = temp
swap(结点->左子树)
swap(结点->右子树)
End
四、功能模块程序流程图
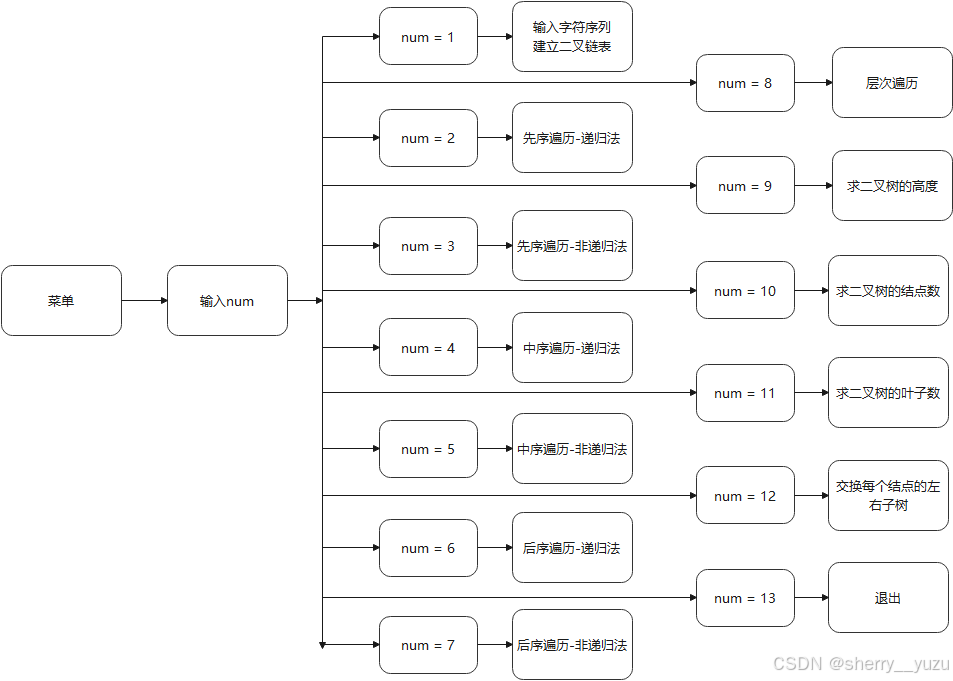
1. 功能选择菜单
说明:菜单功能首先提示用户输入数字。输入数字1,提示用户输入二叉树的每个结点值,以此建立二叉链表;输入数字2,提示输出的结果为“先序遍历二叉树-递归”;输入数字3,提示输出的结果为“先序遍历二叉树-非递归”;输入数字4,提示输出的结果为“中序遍历二叉树-递归”;输入数字5,提示输出的结果为“中序遍历二叉树-非递归”;输入数字6,提示输出的结果为“后序遍历二叉树-递归”;输入数字7,提示输出的结果为“后序遍历二叉树-非递归”;输入数字8,提示输出的结果为“层次遍历”;输入数字9,提示输出的结果为“二叉树的高度”;输入数字10,提示输出的结果为“二叉树的结点数”;输入数字11,提示输出的结果为“二叉树的叶子数”;输入数字12,完成交换二叉树的每个结点的左子树和右子树,提示用户“交换成功!可以通过选择遍历方法来查看交换后的遍历结果”;输入数字13,系统退出,提示用户“退出成功!”;
2. 输入字符序列 创建二叉链表
说明:该函数目的为建立二叉链表,提醒用户输入二叉树的每个结点的序列,如“AB#D##C##”,即可生成一个以链表为存储结构的二叉树,之后可以通过遍历方法来查看二叉树的构造结果。
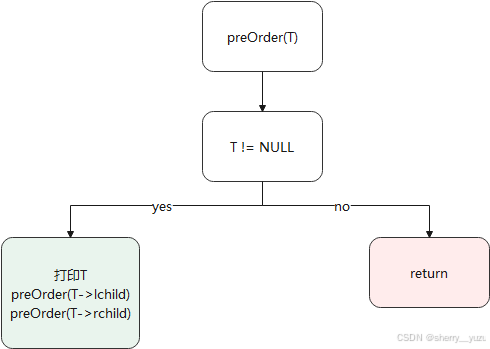
3. 先序遍历-递归法
说明:该函数为实现二叉树的递归法的先序遍历功能,返回值为二叉树的前序遍历结果,传入根节点开始调用即可输出二叉树的先序遍历结果。
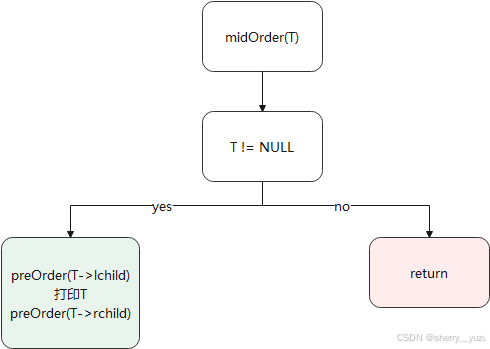
4. 中序遍历-递归法
说明:该函数为实现二叉树的递归法的中序遍历功能,返回值为二叉树的中序遍历结果,传入根节点开始调用即可输出二叉树的中序遍历结果。
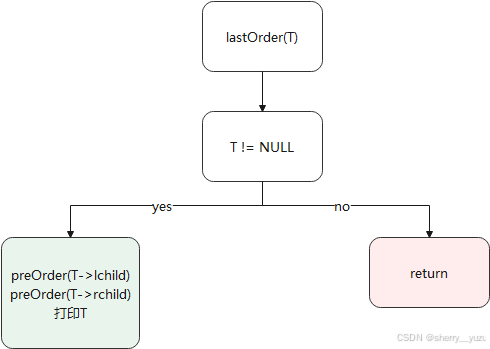
5. 后序遍历-递归法
说明:该函数为实现二叉树的递归法的后序遍历功能,返回值为二叉树的后序遍历结果,传入根节点开始调用即可输出二叉树的后序遍历结果。
6. 先序遍历-非递归法
说明:该函数为实现二叉树的非递归法的先序遍历功能,返回值为二叉树的前序遍历结果,传入根节点开始调用即可输出二叉树的先序遍历结果,与递归法的先序遍历结果一样。
7. 中序遍历-非递归法
说明:该函数为实现二叉树的非递归法的中序遍历功能,返回值为二叉树的中序遍历结果,传入根节点开始调用即可输出二叉树的中序遍历结果,与递归法的中序遍历结果一样。
8. 后序遍历-非递归法
说明:该函数为实现二叉树的非递归法的后序遍历功能,返回值为二叉树的后序遍历结果,传入根节点开始调用即可输出二叉树的后序遍历结果,与递归法的后序遍历结果一样。
9. 层次遍历
说明:该函数为实现二叉树的层次遍历功能,返回值为二叉树的层次遍历结果,传入根节点开始调用即可输出二叉树的层次遍历结果。
10. 求二叉树的高度
说明:该函数为实现求二叉树的高度功能,返回值为二叉树的高度,传入根节点开始调用即可输出二叉树的高度。
11. 求二叉树的结点数
说明:该函数为实现求二叉树的结点数功能,返回值为二叉树的结点数,传入根节点开始调用即可输出二叉树的结点数。
12. 求二叉树的叶子数
说明:该函数为实现求二叉树的叶子数功能,返回值为二叉树的叶子数,传入根节点开始调用即可输出二叉树的叶子数。
13. 交换二叉树每个结点的左子树和右子树
说明:该函数为实现交换二叉树的每个结点的左子树与右子树的功能,传入已有的二叉链表的二叉树的根节点开始调用,即可交换二叉树的每个结点的左子树和右子树,交换成功后,用户通过调用遍历方法即可查看交换完成后的二叉树的遍历结果。
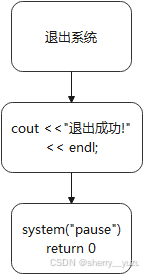
14. 退出
说明:该功能为退出系统功能,调用后即可退出系统,并得到提示“退出成功!”。
五、实验结果
1. 菜单功能
分析:该菜单通过序号1-13来实现不同的有关二叉树的功能,通过提示用户“请输入您要选择的计算”,来引导用户输入1-13的数字来获取想要的结果。
2. 建立二叉链表:
分析:输入数字1后进入该输入字符序列,建立二叉链表的功能。首先提示用户输入二叉树各结点的值,例如AB#D##C##,来建立二叉树,接着继续提示用户选择想要的计算。用户可以通过选择遍历算法来查看二叉树的建立结果。
3. 先序遍历-递归算法:
分析:输入数字2后进入该先序遍历-递归算法的功能,提示先序遍历二叉树-递归的结果为什么,接着提示用户继续选择想要实现的运算。该结果应该与先序遍历-非递归算法的输出结果一致。
4. 先序遍历-非递归算法:
分析:输入数字3后进入该先序遍历-非递归算法的功能,提示先序遍历二叉树-非递归的结果为什么,接着提示用户继续选择想要实现的运算。经结果检验,该结果确实与先序遍历-递归算法的输出结果一致。
5. 中序遍历-递归算法:
分析:输入数字4后进入该中序遍历-递归算法的功能,提示中序遍历二叉树-递归的结果为什么,接着提示用户继续选择想要实现的运算。该结果应该与中序遍历-非递归算法的输出结果一致。
6. 中序遍历-非递归算法:
分析:输入数字5后进入该中序遍历-非递归算法的功能,提示中序遍历二叉树-非递归的结果为什么,接着提示用户继续选择想要实现的运算。经结果检验,该结果确实与中序遍历-非递归算法的输出结果一致。
7. 后序遍历-递归算法:
分析:输入数字6后进入该后序遍历-递归算法的功能,提示后序遍历二叉树-递归的结果为什么,接着提示用户继续选择想要实现的运算。该结果应该与后序遍历-非递归算法的输出结果一致。
8. 后序遍历-非递归算法:
分析:输入数字7后进入该后序遍历-非递归算法的功能,提示后序遍历二叉树-非递归的结果为什么,接着提示用户继续选择想要实现的运算。经结果检验,该结果确实与后序遍历-递归算法的输出结果一致。
9. 层次遍历:
分析:输入数字8后进入该通过队列实现层次遍历的功能,提示层次遍历二叉树的结果为什么,接着提示用户继续选择想要实现的运算。
10. 求二叉树的高度:
分析:输入数字9后进入该通过队列实现求二叉树的高度的功能,提示二叉树的高度的结果为什么,接着提示用户继续选择想要实现的运算。
11. 求二叉树的结点数:
分析:输入数字10后进入该通过队列实现求二叉树的结点数的功能,提示二叉树的结点数的结果为什么,接着提示用户继续选择想要实现的运算。
12. 求二叉树的叶子数:
分析:输入数字11后进入该通过队列实现求二叉树的叶子数的功能,提示二叉树的叶子数的结果为什么,接着提示用户继续选择想要实现的运算。
13. 交换二叉树每个结点的左右子树:
分析:输入数字12后进入该交换二叉树的每个结点的左右子树的功能,提示用户交换成功,接着提示用户可以继续选择遍历算法来查看二叉树交换左右子树后的遍历结果。
分析:交换成功后,通过调用先序,中序,后序遍历的结果来看,遍历结果已经改变,结果正是原子树AB#D##C##将各结点左右子树交换后所得到的遍历结果。
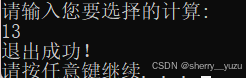
14. 退出:
分析:输入数字13后进入该退出系统的功能,提示用户退出成功。退出成功后,不会再出现提示用户继续输入想要选择的运算。
六、算法分析
1. 遍历的递归算法:前序,中序,后序的算法都是通过递归调用传入左子树及右子树调用自身来实现,根据前、中、后来决定打印根结点的时机。
2. 遍历的非递归算法:核心是通过栈的运用来实现。前序思想是从根结点开始找到最左下角的结点,若结点不为空,则将这期间走过的结点入栈,将当前指针变为当前结点的左子树,重复上述操作,以此找到最左下角的结点。当左边的结点都找完则开始找右边,若栈顶不为空,则结点为栈顶元素,栈顶元素出栈,将当前指针变为当前结点的右子树,重复上述操作。
中序思想与前序思想大致相同,差别在于前序是在每次找最左结点时即打印根结点的元素,而中序是在找右结点时打印根结点的元素。
后序核心是要设立一个结点是否已经被访问过的标志。首先找到最左边的结点,不断将结点入栈,再将指针变为当前结点的左子树,重复上述操作。找到最左下角的结点后即开始回退,遇到根就判断根的左右是否被访问过或为空,若右子树已经被访问了或为空,则打印该右结点。若右结点存在且未被访问过,则重复找到最左边的结点的操作。继续进入循环。
3. 层次遍历:思想是把结点依次入队列再出列,输出该节点。判断该节点是否有孩子,若有,先将左孩子递归调用层次遍历的函数,重复入队出队、判断是否有孩子的操作。再将右孩子递归调用层次遍历的函数,重复入队出队、判断是否有孩子的操作。
4. 求二叉树的高度:思想是传入树的根结点,用该结点的左子树和右子树递归调用求高度的方法,从最下面开始依次向上输出左子树和右子树的高度,并返回左高与右高之间的较大者,将最后返回的结果再加1(即加上根结点的高度),即得到树的真正高度。
5. 求二叉树的结点数及叶子数:求结点数的思想是判断结点是否有左孩子或有右孩子,若满足其实一个,则令结点数++。求叶子数则是判断结点是否无左孩子且无右孩子,若满足则令叶子数++。
6. 交换左右子树:思想是通过临时变量temp来交换节点的左右子树,再利用结点的左右子树,递归调用该交换方法。
七、操作说明
编译后先出现一个菜单,1-13有文字信息描述二叉树的相关算法,提示用户输入1-13之间的数字。
输入数字1,提示用户输入二叉树的每个结点值,以此建立二叉链表;
输入数字2,提示输出的结果为“先序遍历二叉树-递归”;
输入数字3,提示输出的结果为“先序遍历二叉树-非递归”;
输入数字4,提示输出的结果为“中序遍历二叉树-递归”;
输入数字5,提示输出的结果为“中序遍历二叉树-非递归”;
输入数字6,提示输出的结果为“后序遍历二叉树-递归”;
输入数字7,提示输出的结果为“后序遍历二叉树-非递归”;
输入数字8,提示输出的结果为“层次遍历”;
输入数字9,提示输出的结果为“二叉树的高度”;
输入数字10,提示输出的结果为“二叉树的结点数”;
输入数字11,提示输出的结果为“二叉树的叶子数”;
输入数字12,完成交换二叉树的每个结点的左子树和右子树,提示用户“交换成功!可以通过选择遍历方法来查看交换后的遍历结果”;
输入数字13,系统退出,提示用户“退出成功!”;