空间相关分析(一) 空间权重矩阵

之前的博客分享了各行政区shp文件的制作方法，在拿到shp文件后就可以进行空间相关分析啦。今天来介绍一下相关理论的基础——空间权重矩阵的创建。

邻接矩阵
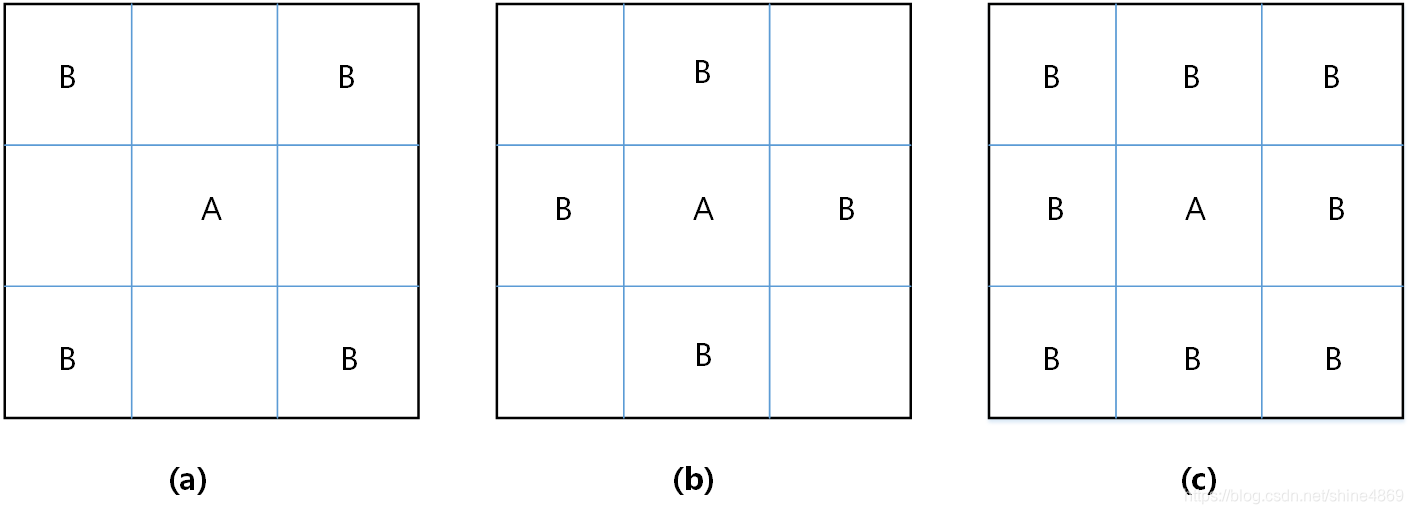
根据空间相邻关系，相邻既可以是有共同边界又可以是有共同顶点。因此，可分为三种类型：Bishop邻接、Rock邻接、Queen邻接，分别如图(a)，(b)，©所示

图a中A与所有的B都是共顶点连接
图b中A与所有的B都是共领边连接
图c中A与所有的B既是共顶点连接又是共领边连接
不难看出，Queen邻接是Bishop邻接和Rock邻接的结合。一般实际操作过程中，多数都是选Queen连接。根据连接方式，我们即可构建如下空间权重矩阵 $W$ 来反映区县间的邻接关系：
$W=\begin{bmatrix} w_{11} & w_{12} & \dots & w_{1n}\\ w_{21} & w_{22} & \dots & w_{2n} \\ \vdots & \vdots & \vdots & \vdots \\ w_{n1} & w_{n2} & \dots & w_{nn} \end{bmatrix}$
其中， $w_{ij}=\begin{cases} 1, & \text{区县$\mathit{i}$与区县$\mathit{j}$相邻时} \\ 0, & \text{区县$\mathit{i}$与区县$\mathit{j}$不相邻时} \end{cases}$
特别说明：当 $i=\mathit{j}$ 时，记 $w_{ij}=0$
不难看出，矩阵W是个对称阵，即 $W^T=W$
距离矩阵
        空间单元间除了相邻关系，还有可用距离进行描述。在空间计量经济学中，可分为狭义距离和广义距离。狭义距离通常指两个区域的质心距离或者行政中心距离，构建方式如下：
$W=\begin{bmatrix} 0 & \frac{1}{d_{1,2}} & \dots & \frac{1}{d_{1,n}}\\ \frac{1}{d_{2,1}} & 0 & \dots & \frac{1}{d_{2,n}} \\ \vdots & \vdots & \vdots & \vdots \\ \frac{1}{d_{n,1}} & \frac{1}{d_{n,2}} & \dots & 0 \end{bmatrix}$
其中， $d_{ij}$ 表示区域 $\mathit{i}$ 与区域 $\mathit{j}$ 之间质心距离(或者行政中心距离)。故距离越远，空间权重系数越小，空间相关性越差。

        广义距离则包括多种形式的虚拟距离，比如：经济距离。例如：在研究区域经济聚集现象时，很多情况下地理位置相邻并不能代表相关性相同。例如：浙江省、江苏省、安徽省三者相领接，但浙江省和江苏省的经济实力明显要高于安徽省，则我们可认为浙江与江苏经济距离更近，而安徽与浙江、江苏的经济距离较远，故前者的空间权重系数要较后者大，空间相关性更强。构建方式如下：
$W=\begin{bmatrix} 0 & \frac{1}{|Y_{1}-Y_{2}|} & \dots & \frac{1}{|Y_{1}-Y_{n}|}\\ \frac{1}{|Y_{2}-Y_{1}|} & 0 & \dots & \frac{1}{|Y_{2}-Y_{n}|} \\ \vdots & \vdots & \vdots & \vdots \\ \frac{1}{|Y_{n}-Y_{1}|} & \frac{1}{|Y_{n}-Y_{2}|} & \dots & 0 \end{bmatrix}$
        其中， $Y_{i}$ 和 $Y_{j}$ 代表各区域的经济发展水平，则 $Y_{i}-Y_{j}|$ 则代表两者的经济距离。（一般文献里面用的比较多的是人均GDP来衡量地区发展水平，如果更深入地讨论的话可以使用主成分分析、层次分析、熵值法等方法构建综合经济指标体系），具体的构建方式可参考经济距离矩阵Python构建

Geoda创建空间权重矩阵

理论说完了，开始实际操作吧。Geoda创建空间权重矩阵还是比较简单的，这里使用的是Geoda1.14中文版本，以重庆市为例：
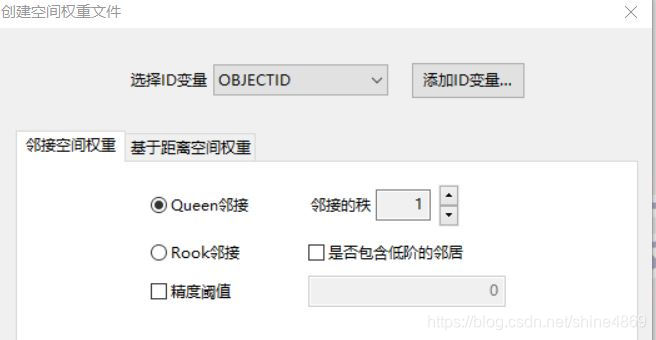
工具——空间权重管理——创建——选择ID变量
！注意，这里的ID变量必须是一个ID对应一个区县
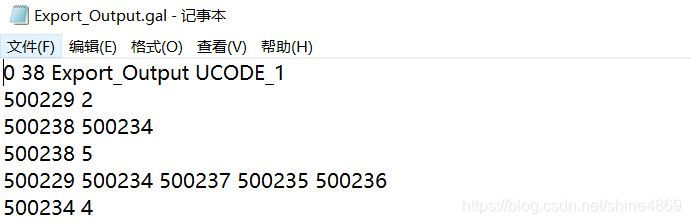
在这里插入图片描述
根据需要选择对应的连接方式即可。邻接型生成的是gal文件，距离型生成的是gwt文件。这里以Queen连接生成的gal数据格式说明：

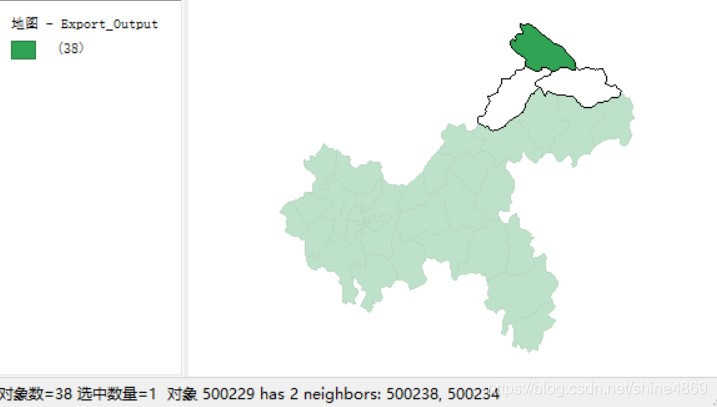
第一行38代表重庆市区县总个数，500229是区县对应的ID，它有两个相邻区县，分别是500238和500234；以此类推，500238有5个相邻的区县分别为500229，500234，500237，500235，500236。以地图的方式显示如下：
在这里插入图片描述
当然，gal这种数据格式定义的权重矩阵并不是前面定义所提到的 $n * n$ 形式的矩阵。我们可以用R进行转化，转化代码如下：

gal2mat <- function(gal, row.st = TRUE) {
  gal <- scan(gal, skip = 1)
  neighbors <- list()
  while(TRUE) {
    nb <- gal[2]
    if(nb != 0) {
      neighbors[[as.character(gal[1])]] <- as.character(gal[3:(2+nb)])
    } else {
      warning(paste("Unit", gal[1], "has no neighbor."))
      neighbors[[as.character(gal[1])]] <- 0
    }
    gal <- gal[-(1:(2+nb))]
    if(length(gal) == 0) break
  }
  n <- length(neighbors)
  swm <- matrix(0, n, n)
  dnames <- names(neighbors)
  dimnames(swm) <- list(dnames, dnames)
  for(i in dnames) {
    swm[i, neighbors[[i]]] <- 1
  }
  if(row.st) {
    swm <- apply(swm, 1, function(x) {
      if(sum(x) != 0) return(x/sum(x)) else {
        warning("The sum of row is 0.")
        return(x)
      }
    })
    swm <- t(swm)
  }
  return(swm)
}
library(spdep)
mynb <- read.gal("Export_Output.gal",override.id=TRUE)
spmat1 <- nb2mat(mynb, zero.policy=TRUE)
spmat2 <- gal2mat("Export_Output.gal",row.st=FALSE)
write.csv(spmat2, "spmat.csv")

在这里插入图片描述

Arcgis创建空间权重矩阵

Arcgis创建空间权重矩阵时，shp文件必须放在英文路径下，否则会报错！

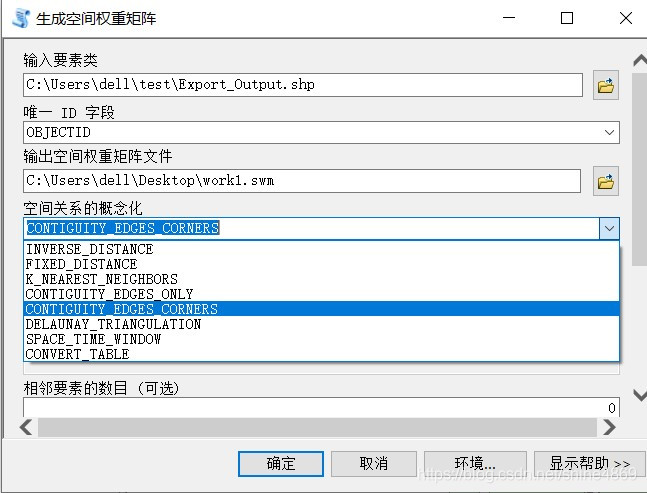
ArcToolBox—空间统计工具—空间关系建模—生成空间权重矩阵
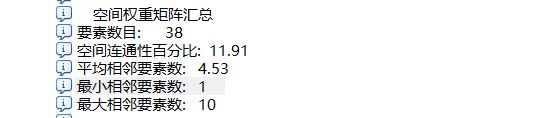
在这里插入图片描述
这里的CONTIGUITY_EDGES_ONLY、CONTIGUITY_EDGES_CORNERS对应的就是Rock连接和Queen连接。生成权重矩阵信息如下：

在这里插入图片描述
最终生成的是swm文件，还需要将其转化为表。

空间统计工具——工具——将空间权重矩阵转化为表

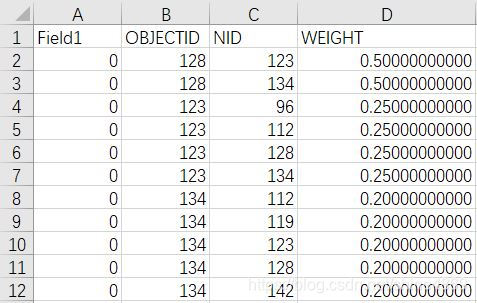
在这里插入图片描述
生成的表是dbf文件，先用excel打开查看数据情况

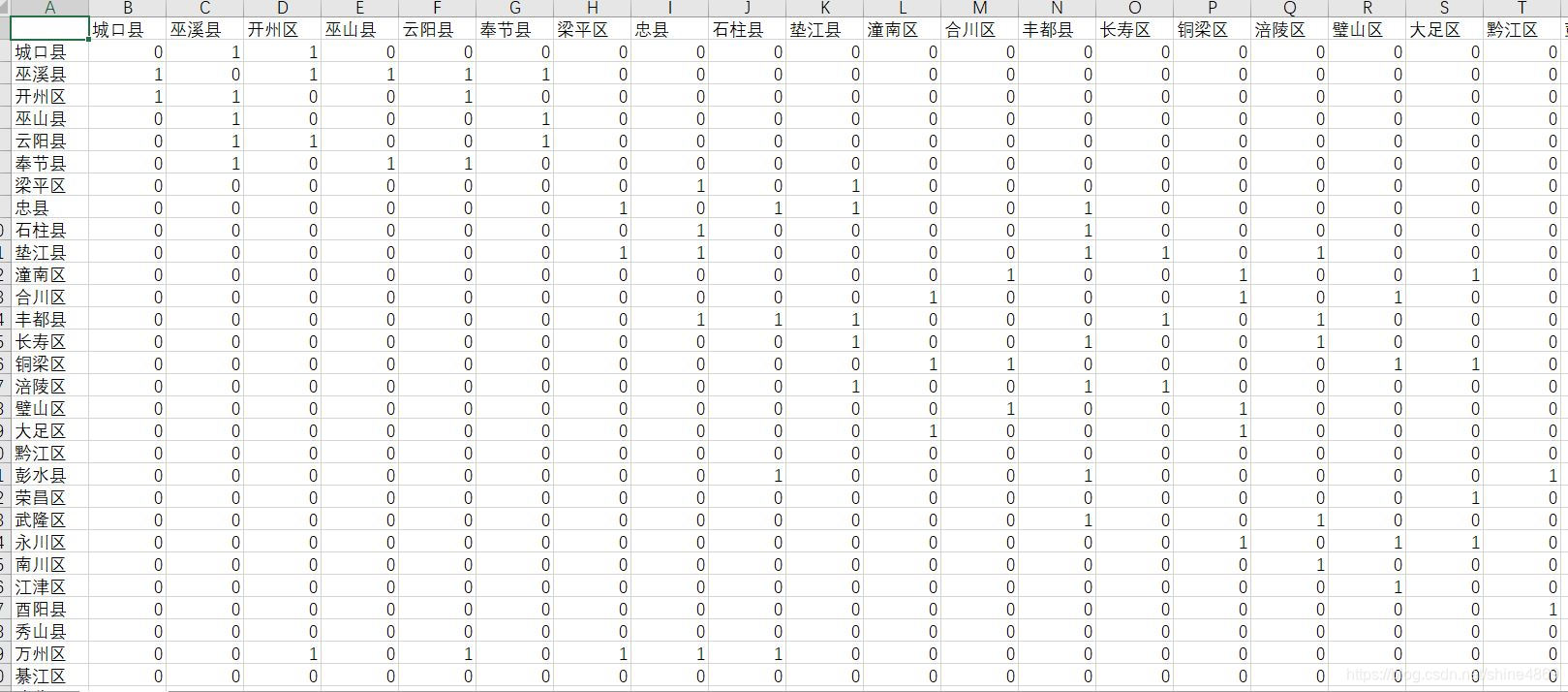
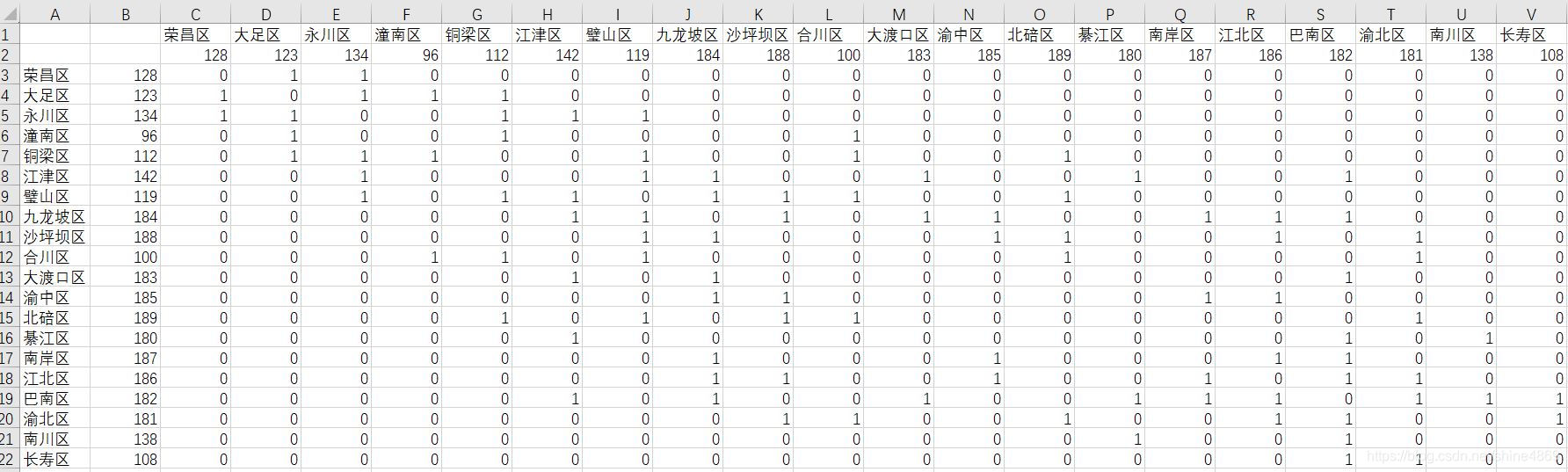
OBJECTID即是区县的代码，这里和gal文件表示邻接的方式有些区别。即代号为128的区县有两个领接的区县123和134。
同样可以使用R语言转为 $n * n$ 的矩阵，如下所示：

swm2mat <- function(dbf) {
  library(foreign)
  swm <- read.dbf(dbf)
  units <- as.character(unique(swm[,2]))
  n <- length(units)
  mat <- matrix(0, nr=n, nc=n)
  dimnames(mat) <- list(units, units)
  i <- as.character(swm[,2])
  j <- as.character(swm[,3])
  w <- swm[,4]
  Map(function(i,j,w) mat[i,j] <<- w, i, j, w)
  return(mat)
}
spmat <- swm2mat("province31_swm.dbf")

在这里插入图片描述
(最后吐槽一下，本来想写博客只是将自己学的知识整理一下。没想到论文检测的时候，居然检测到自己的博客，简直要吐血！！

参考文献：
1.漫谈空间权重矩阵W
2.将gal权重文件转成n-by-n矩阵
3.将swm权重文件转为n-by-n矩阵