Bootstrap

力扣每日一题合集

3211. 生成不含相邻零的二进制字符串 - 力扣（LeetCode）

class Solution {
public:
   vector<string> validStrings(int n) 
   {
       vector<string> ans;
       ans.emplace_back("0");
       ans.emplace_back("1");
       for(int i = 1; i < n; i++)
       {
            int m = ans.size();
            for(int j = 0; j < m; j++)
            {
                auto x = ans[j].back();
                if('1' == x)ans.emplace_back(ans[j] + "0");
                ans[j] += '1';
            }
       }
       return ans;
   }
};

1016. 子串能表示从 1 到 N 数字的二进制串 - 力扣（LeetCode）

解一:暴力(bitset模板)

class Solution {
public:
    bool queryString(string s, int n) 
    {
        for(int i = 1;i <= n; i++)
        {
            auto str = bitset<32>(i).to_string();
            str = str.substr(str.find('1'));
            if(s.find(str) == s.npos)return false;
        }
        return true;
    }
};

解二:哈希表

class Solution {
public:
    bool queryString(string s, int n)
    {
        unordered_set<int>ans;
        for(int i = 0;i < s.size(); i++)
        {
            int x = s[i] ^ 48;
            if(!x)continue;
            for(int j = i + 1;x <= n;j++)
            {//提问1:为什么是j = i + 1 ??? 
                ans.insert(x);
                x = (x << 1) | (s[j] ^ 48);//提问二:这样赋值的意义?
                if(j == s.size() )break;
            }
        }
        return ans.size() == n;
    }
};

解三:滑动窗口 + 哈希表 + 数学

分析:

1:列表

11
210
311
4100
5101
6110
7111
81000
91001
101010
111011
121100
131101
141110
151111

class Solution {
public:
    bool help(const string& s, int bitlen, int min, int max) 
    {
        unordered_set<int> st;
        int t = 0;
        for (int r = 0; r < s.size(); ++r)
        {
            t = (t << 1) + (s[r] ^ 48);
            if (r >= bitlen)
                t -= (s[r - bitlen] ^ 48) << bitlen;
            if (r >= bitlen - 1 && t >= min && t <= max)
                st.insert(t);
        }
        return st.size() == max - min + 1;
    }

    bool queryString(string s, int n) 
    {
        if (n == 1)  return s.find('1') != s.npos;
        int bitlen = 31 - __builtin_clz(n);
        if (s.size() < (1 << (bitlen - 1)) + bitlen - 1 || s.size() < n - (1 << bitlen) + bitlen + 1) return false;
        return help(s, bitlen, 1 << (bitlen - 1), (1 << bitlen) - 1) && help(s, bitlen + 1, 1 << bitlen, n);
    }
};

 122. 买卖股票的最佳时机 II - 力扣（LeetCode）

//由于当天买可以当天卖 == >> 每天都更新状态
//状态一:   当前卖亏本 == >> 穿越到昨天卖出 然后买今天(即理解为昨天买了昨天就卖)
//状态二:   当前卖盈利 == >> 卖出 == >> 更新答案
//状态三:   当前卖亏本但是卖出前些天的盈利 == >> 穿越到昨天不卖出,今天卖出 == >> 更新答案
class Solution {
public:
    int maxProfit(vector<int>& prices) 
    {
        int ans = 0;
        int pre = INT_MAX;
        int sell = pre;
        int profit = 0;
        for(auto x : prices)
        {
            if(x > pre)
            {//可以出售
                ans += x - pre;
                profit = x - pre;
                pre = sell = x;
            }
            else
            {//出售亏本
                if(x - sell > profit)
                {
                    ans = ans - profit + x - sell;
                    profit = x - sell;
                }
                else
                {
                    pre = x;
                }
            }
        }
        return ans;
    }
};

307. 区域和检索 - 数组可修改 - 力扣（LeetCode）

int init = []()
{
    cin.tie(0) -> sync_with_stdio(false);
    return 0;
}();

class NumArray {
public:
    NumArray(vector<int>& nums) : sum(nums.size() + 1, 0), num(nums), n(nums.size()) 
    {
        for(int i = 0;i < n;i++)
        add(i + 1,nums[i]);
    }

    int lowbit(int x)
    {
        return x & -x;
    }

    void add(int pos, int val)
    {
        for(; pos <= n; pos += lowbit(pos))
        sum[pos] += val;
    }

    void update(int index, int val) 
    {
        add(index + 1, val - num[index]);
        num[index] = val;
    }
    
    int ask(int x)
    {
        int ans = 0;
        for(; x > 0; x -= lowbit(x))
        ans += sum[x];
        return ans;
    }

    int sumRange(int left, int right) 
    {
        return ask(right + 1) - ask(left);
    }
private:
vector<int>sum;
vector<int>&num;
int n;
};

/**
 * Your NumArray object will be instantiated and called as such:
 * NumArray* obj = new NumArray(nums);
 * obj->update(index,val);
 * int param_2 = obj->sumRange(left,right);
 */

354. 俄罗斯套娃信封问题 - 力扣（LeetCode）

示例 1：

输入：envelopes = [[5,4],[6,4],[6,7],[2,3]]
输出：3
解释：最多信封的个数为 3, 组合为: [2,3] => [5,4] => [6,7]。

示例 2：

输入：envelopes = [[1,1],[1,1],[1,1]]
输出：1

提示：

  • 1 <= envelopes.length <= 105
  • envelopes[i].length == 2
  • 1 <= wi, hi <= 105

首先按照朴素的dp思想

先定义每一个信封的状态,无非是选择或者不选择。

int dp[n]; 选择第i个信封最多可以嵌套的数量.

在按照

  sort(envelopes.begin(),envelopes.end(),[&](auto x, auto y)
        {return x[0] == y[0] ? x[1] < y[1] : x[0] < y[0];});

规则的排序下,可知道

若 第i个信封可以完全包裹上一个信封则进行

                if(envelopes[i][1] > envelopes[j][1] && envelopes[i][0] > envelopes[j][0])
                {
                    dp[i] = max(dp[i], dp[j] + 1);
                }

否则将 dp[i]置为1

为什么置为1 ? 

因为不存在当第i个信封能完全包裹一个信封的情况下会有不选择该信封的ans > 选择该信封的ans

那么可以认为,要么第i个信封能包裹信封,要么将第i个信封作为一个新的开头

 可得最初版的线型dp解

class Solution {
public:
    int maxEnvelopes(vector<vector<int>>& envelopes) 
    {
        sort(envelopes.begin(),envelopes.end(),[&](auto x, auto y)
        {return x[0] == y[0] ? x[1] < y[1] : x[0] < y[0];});
        int n = envelopes.size();
        int dp[n];
        memset(dp, 0, sizeof dp);
        dp[0] = 1;
        for(int i = 1; i < n; i++)
        {
            for(int j = i - 1; j >= 0; j--)
            {
                if(envelopes[i][1] > envelopes[j][1] && envelopes[i][0] > envelopes[j][0])
                {
                    dp[i] = max(dp[i], dp[j] + 1);
                }
            }
            if(0 == dp[i])dp[i] = 1;
        }
        int ans = 0;
        for(int i = 0; i < n;i++)
        ans = max(ans, dp[i]);
        return ans;
    }
};

 以上代码的时间复杂度为排序O(nlogn) + O(n ^ 2)

显然对于 1 <= envelopes.length <= 105 是远远不够的

现在看看核心代码

        for(int i = 1; i < n; i++)
        {
            for(int j = i - 1; j >= 0; j--)
            {
                if(envelopes[i][1] > envelopes[j][1] && envelopes[i][0] > envelopes[j][0])
                {
                    dp[i] = max(dp[i], dp[j] + 1);
                }
            }
            if(0 == dp[i])dp[i] = 1;
        }

是不是很像求最长递减子序列?

只不过是先对长or宽排序之后对宽or长序列求最长子序列即可

那我们直接用二分优化求最长子序列的方法做即可

class Solution {
public:
    int maxEnvelopes(vector<vector<int>>& envelopes) 
    {
        sort(envelopes.begin(),envelopes.end(),[&](auto x, auto y)
        {return x[0] == y[0] ? x[1] > y[1] : x[0] < y[0];});
        int n = envelopes.size();
        vector v = {0};
        for(int i = 0; i < n; i++)
        {
            int k = envelopes[i][1];
            if(k > v.back())
            {
                v.emplace_back(k);
            }
            else
            {
                auto it = lower_bound(v.begin(),v.end(),k);
                *it = k;
            }
        }
        return v.size() - 1;
    }
};

2731. 移动机器人 - 力扣（LeetCode）

 

暴力模拟如下 :

class Solution {
public:
    const int mod = 1e9 + 7;
    int sumDistance(vector<int>& nums, string s, int d) 
    {
        using i64 = long long;
        int n = nums.size();
        while(d--)
        {
            for(int i = 0;i < n;i++)
            {
                nums[i] += (s[i] == 'R' ? 1 : -1);
                if(i && nums[i] == nums[i - 1])
                swap(s[i], s[i - 1]);
            }
        }
        i64 ans = 0;
        for(int i = 0; i < n; i++)
        {
            for(int j = i + 1;j < n;j++)
            ans = (ans % mod + (abs(v[i] - v[j]) % mod)) % mod;
        }
        return ans; 
    }
};

看数据范围d == 1e9

可见该题解在处理d秒时的时间复杂度应当不超过O(n)

因此:上解需要优化

 当我们碰撞的时候:

                if(i && nums[i] == nums[i - 1])
                swap(s[i], s[i - 1]);

交换俩者的方向,那也等于交换俩个机器人的效果,于是我们可以忽略碰撞影响,直接求d秒无碰撞的相对位置即可。

举一个简单的例子:

A = 0 == >> R

B = 2 == >> L

d = 10;

在1秒的时候交换方向

A = 1 == >> L

B = 1 == >> R

10s后:

A = -8 == >> L

B =  10 == >> R;

直接求相对距离

A = 10 == >> R

B = -8 == >> L

因此直接求d秒无碰撞的相对位置对最终答案无影响

此时: 由数据范围nums最大可为2e9,d 最大为1e9 >> 2147483647

爆int,需要i64数据类型进行存储

 可得:

class Solution {
public:
    const int mod = 1e9 + 7;
    int sumDistance(vector<int>& nums, string s, int d) 
    {
        using i64 = long long;
        int n = nums.size();
        vector<i64> v(n);
        for(int i = 0;i < n; i++)
        v[i] = nums[i] + (s[i] == 'R' ? d : -d);
        i64 ans = 0;
        for(int i = 0; i < n; i++)
        {
            for(int j = i + 1;j < n;j++)
            ans = (ans % mod + (abs(v[i] - v[j]) % mod)) % mod;
        }
        return ans; 
    }
};

再看数据范围 

 n的范围为[2,1e5]  

仅看ans求值的第一轮循环1e5 * (1e5 - 1)显然超时

对于ans的求值过程有这么一种情况

对于任意 i [0,n]前有i个数,后有n - i个数 == >> i * (n - i)个数对都会进行一次加(v[i] - v[i- 1])的值

可得:

class Solution {
public:
    const int mod = 1e9 + 7;
    int sumDistance(vector<int>& nums, string s, int d) 
    {
        using i64 = long long;
        int n = nums.size();
        vector<i64> v(n);
        for(int i = 0;i < n; i++)
        v[i] = nums[i] + (s[i] == 'R' ? d : -d);
        sort(v.begin(),v.end());
        i64 ans = 0;
        for (int i = 1; i < n; i++) 
        {
            ans = ((v[i] - v[i - 1]) * i % mod * (n - i) + ans) % mod;
        }
        return ans; 
    }
};

 

121. 买卖股票的最佳时机 - 力扣（LeetCode）

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int ans = 0;
        int pre = prices[0];
        for(auto & x : prices)
        {
            pre = min(pre,x);
            ans = max(ans, x - pre);
        }
        return ans;
    }
};

64. 最小路径和 - 力扣（LeetCode）

class Solution {
public:
    int minPathSum(vector<vector<int>>& grid) 
    {
        int m = grid.size();
        int n = grid[0].size();
        for(int i = 0; i < m; i++)
        {
            for(int j = 0; j < n; j++)
            {
                if(0 == i && 0 == j)continue;
                if(0 == i) grid[i][j] += grid[i][j - 1];
                else if(0 == j)grid[i][j] += grid[i - 1][j];
                else grid[i][j] += min(grid[i][j - 1],grid[i - 1][j]);
            }
        }         
        return grid[m - 1][n - 1];
    }
};

62. 不同路径 - 力扣（LeetCode）

class Solution {
public:
    int uniquePaths(int m, int n) {
        using i64 = int64_t;
        i64 ans = 1;
        int x = n, y = 1;
        while(y < m)
        {
            ans = ans * x / y;
            x++;y++;
        }
        return ans;
    }
};

63. 不同路径 II - 力扣（LeetCode）

 不额外开数组的方法

class Solution {
public:
    int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) 
    {
        int m = obstacleGrid.size();
        int n = obstacleGrid[0].size();
        for(int i = 0; i < m; i++)
        {
            for(int j = 0; j < n;j++)
            {
                obstacleGrid[i][j] ^= 1;
                if(!i && !j)continue;
                else if(!i) 
                {
                    if(obstacleGrid[i][j] == 0)continue;
                    obstacleGrid[i][j] += obstacleGrid[i][j - 1] - 1;
                }
                else if(!j)
                {
                    if(obstacleGrid[i][j] == 0)continue;
                    obstacleGrid[i][j] += obstacleGrid[i - 1][j] - 1;
                }
                else 
                {
                    if(obstacleGrid[i][j] == 0)continue;
                    obstacleGrid[i][j] += (obstacleGrid[i][j - 1] + obstacleGrid[i - 1][j]) - 1;
                }
            }
        }
        return obstacleGrid[m - 1][n - 1];
    }
};

    或者额外开一个数组

class Solution {
public:
    int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) 
    {
        int n = obstacleGrid.size(), m = obstacleGrid.at(0).size();
        vector <int> dp(m, 0);
        dp[0] = 1 - obstacleGrid[0][0];
        for (int i = 0; i < n; i++) 
        {
            for (int j = 0; j < m; j++) 
            {
                if(obstacleGrid[i][j] == 1)
                dp[j] = 0;
                else if(j && obstacleGrid[i][j - 1] == 0)//无需判断j == 0
                dp[j] += dp[j - 1];   
            }
        }
        return dp.back();
    }
};

2136. 全部开花的最早一天 - 力扣（LeetCode）

 简单的贪心然后结构体排序(也可以创建数组记录位置访问)

class Solution {
public:
    struct node
    {
        int id, p, g;
        node(int a,int b, int c) : id(a), p(b), g(c){};
    };
    int earliestFullBloom(vector<int>& plantTime, vector<int>& growTime) 
    {
        vector<node>v;
        int n = plantTime.size();
        for(int i = 0; i < n; i++)
        v.emplace_back(i,plantTime[i],growTime[i]);
        sort(v.begin(),v.end(),[&](auto x,auto y) {return x.g > y.g;});
        int ans = 0, pre = 0;
        for(auto x : v)
        {
            ans = max(ans, pre + x.p + x.g);
            pre += x.p;
        }
        return ans;
    }
};

605. 种花问题 - 力扣（LeetCode）

动态规划

class Solution {
public:
    bool canPlaceFlowers(vector<int>& flowerbed, int n) 
    {
        int m = flowerbed.size();
        if(1 == m)return !flowerbed[0] >= n;
        else if(2 == m)return ((!flowerbed[0] && !flowerbed[1]) >= n);
        int dp[m][2];//第i个位置种|不种最大的收获数
        memset(dp, 0, sizeof dp);
        if(!flowerbed[0] && !flowerbed[1])
        {
            dp[0][1] = 1;
            dp[1][0] = 1;
            dp[1][1] = 1 - flowerbed[2];
        }
        for(int i = 2; i < m - 1; i++)
        {
            if(!flowerbed[i] && !flowerbed[i + 1] && !flowerbed[i - 1])
            {
                dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + 1);
                dp[i][0] = dp[i - 1][1];
            }
            else
            {
                dp[i][1] = max(dp[i - 1][1], dp[i - 1][0]);
                dp[i][0] = max(dp[i - 1][1], dp[i - 2][1]);
            }
        }
        if(!flowerbed[m - 1] && !flowerbed[m - 2])
        {
            dp[m - 1][1] = max(dp[m - 2][0] + 1,dp[m - 2][0]);
            dp[m - 1][0] = max(dp[m - 1][1], dp[m - 2][1]);
        }
        else
        dp[m - 1][0] = max(dp[m - 2][1],dp[m - 2][0]);
        return max(dp[m - 1][0], dp[m - 1][1]) >= n;
    }
};

贪心

class Solution {
public:
    bool canPlaceFlowers(vector<int> &flowerbed, int n) 
    {
        int m = flowerbed.size();
        flowerbed.insert(flowerbed.begin(),0);
        flowerbed.emplace_back(0);
        for(int i = 1; i <= m; i++)
        {
            if(!flowerbed[i] && !flowerbed[i - 1] && !flowerbed[i + 1])
            {
                flowerbed[i] = 1;
                n--;
            }
        }
        return n <= 0;
    }
};

740. 删除并获得点数 - 力扣（LeetCode）

简单分析一下:

每一个数字其实只有2个状态选 or 不

可得预处理每一个数初始状态(不选为0,选为所有x的个数 * x)累加即可

for(auto &x : nums)
   dp[x][1] += x;

每选一个树 i 删去 i + 1 和 i - 1

故我们可以将 i - 1视为 i 的父节点, i + 1视为 i 的子节点(此时思路就向树形dp经典题"参加舞会"一样如果i节点参与,其子节点和父节点不参与)

可得

 for(int i = 2; i <= n;i++)
        {
            dp[i][1] += dp[i - 1][0];
            dp[i][0] += dp[i - 1][1];
        }

再考虑特殊情况:中间断层 1 5 or 任意不连续数字串 

此时对与5 显然 其没有父节点 和 子节点(无法正常转移)

那么倒退4,我们构建4节点,因为其本身不存在选和不选都不影响最终结果

可得

            if(!dp[i][1])
            {
                dp[i][1] = dp[i][0] = mx;
                continue;
            }

由于每一个节点的权值大小不同,对于第i个节点为true的时候有特殊情况(即选的权值不如不选的情况)

可得

                dp[i][1] = max(dp[i][1] + dp[i - 1][0], dp[i - 1][1]);
                dp[i][0] += dp[i - 1][1];

由于题目数据范围为

故进行转移时只用转移1e4次即可 

//using i64 = int64_t;
class Solution {
public:
    const int maxn = 1e4 + 10;
    int dp[10010][2];
    int deleteAndEarn(vector<int>& nums) 
    {
        //视为树形dp(easy版)
        //例如:样例一 == >> 2 3 4
        //样例二 == >> 4 9 4    
        memset(dp, 0, sizeof dp);
        for(auto &x : nums)
        dp[x][1] += x;
        int mx = 0;
        for(int i = 1; i <= 10000; i++)
        {
            if(!dp[i][1])
            {
                dp[i][1] = dp[i][0] = mx;
                continue;
            }
            else
            {
                dp[i][1] = max(dp[i][1] + dp[i - 1][0], dp[i - 1][1]);
                dp[i][0] += dp[i - 1][1];
            }
            mx = max({mx,dp[i][1],dp[i][0]});
        }
        return max(dp[10000][1], dp[10000][0]);
    }
};

 时间复杂度:常数级

1333. 餐厅过滤器 - 力扣（LeetCode）

 简单的按规则排序,去除几个不满足的条件然后排序返回即可

#include<algorithm>
class Solution {
public:
    vector<int> filterRestaurants(vector<vector<int>>& restaurants, int veganFriendly, int maxPrice, int maxDistance) 
    {
        vector<int>ans;
        std::sort(restaurants.begin(),restaurants.end(),[](vector<int>& a,vector<int>& b)
        {
            return a[1] == b[1] ? a[0] > b[0] : a[1] > b[1]; 
        	return true;
        });
        if(veganFriendly)
        for(auto x : restaurants)
        {
            if(!x[2] || x[3] > maxPrice || x[4] > maxDistance)continue;
            ans.emplace_back(x[0]);
        }
        else
        for(auto x : restaurants)
        {
            if( x[3] > maxPrice || x[4] > maxDistance)continue;
            ans.emplace_back(x[0]);
        }
        return ans;
    }
};

1137. 第 N 个泰波那契数 - 力扣（LeetCode）

一题简单的递推,也是没什么好说的

class Solution {
public:
    int tribonacci(int n) {
        std::array<int,3> ans = {0, 1, 1};
        if(n <= 2)
        return ans[n];
        // 0 1 1 2 4 7
        for(int i = 0; i <= n - 3; i++)
        {
            int d = 0;
            for(int j = 0; j < 3; j++)
            {
               // std::cout << ans[j] << " ";
                d += ans[j];
                if(2 - j)ans[j] = ans[j + 1];
            }
          //  std::cout << "\n" << d << " " << "\n";
            ans[2] = d;
        }
        return ans[2];
    }
};

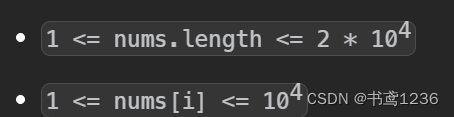
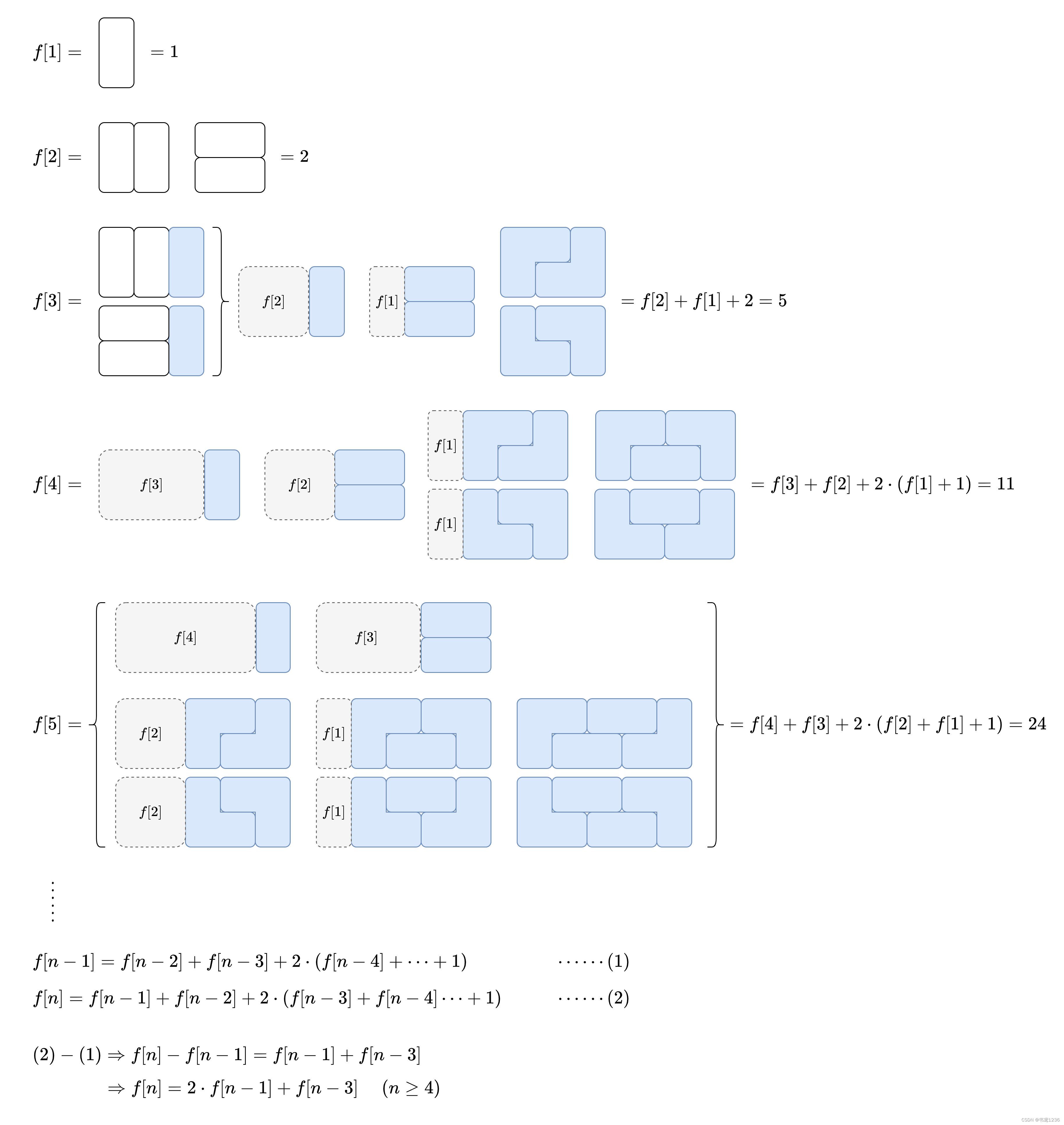
790. 多米诺和托米诺平铺 - 力扣（LeetCode）

方法一:状态压缩dp

class Solution {
public:
    int mod = 1e9 + 7;
    int numTilings(int n) 
    {
        using i64 = int64_t;
        //按列表达状态 00 10 01 11
        i64 dp[n + 1][12];//平铺到第i 列时状态为 …… 的方案数
        memset(dp, 0, sizeof dp);
        dp[0][1 << 1 | 1] = 1;
        for(int i = 1; i <= n;i++)
        {
            dp[i][0] = dp[i - 1][1 << 1 | 1];
            dp[i][1 << 1] = (dp[i - 1][0] + dp[i - 1][1]) % mod;
            dp[i][1] = (dp[i - 1][0] + dp[i - 1][1 << 1]) % mod;
            dp[i][1 << 1 | 1] = (dp[i - 1][0] + dp[i - 1][1] + dp[i - 1][1 << 1 | 1] + dp[i - 1][1 << 1]) % mod;
        }
        return dp[n][1 << 1 | 1] % mod;
    }
};

主要是方法二:学习别人的想法和写法


作者：灵茶山艾府
链接：https://leetcode.cn/problems/domino-and-tromino-tiling/submissions/
来源：力扣（LeetCode）

class Solution {
    const int MOD = 1e9 + 7;
public:
    int numTilings(int n) {
        if (n == 1) return 1;
        long f[n + 1];
        f[0] = f[1] = 1;
        f[2] = 2;
        for (int i = 3; i <= n; ++i)
            f[i] = (f[i - 1] * 2 + f[i - 3]) % MOD;
        return f[n];
    }
};

1653. 使字符串平衡的最少删除次数 - 力扣（LeetCode）

// 动态规划解一
class Solution 
{
public:
    int minimumDeletions(string s) 
    {
        int n = s.size();
        int* dp = new int[s.size()+1];
        fill(dp, dp + n + 1, 0);
        int numb = 0;
        if(s[0]=='b')numb++;
        for (int i = 1; i < n; i++)
        {
            //删除情况:要么是把a之前的b全部删除,要么删掉这个a本身
            if (s[i] == 'a')
            {
                //如果是a,选择删掉之前b或者删掉自己
                dp[i] = min(dp[i - 1] + 1, numb);
            }

            else
            {
                //如果为b状态和前者一样,记录其存在数
                numb++;
                dp[i] = dp[i - 1];
            }
        }
        return dp[n-1];
    }
};

//动态规划解二

class Solution {
public:
    int minimumDeletions(string s) {
        int numb = 0, ans = 0;
        for (auto i : s) {
            if ('a' == i)
            {
                ans = min(ans + 1, numb);
            }
            else
            {
                numb++;
            }
        }
        return ans;
    }
};


//栈区解
class Solution {
public:
    int minimumDeletions(string s)
    {
        stack<char>st;
        int ans = 0;
        for (auto i : s)
         {
            if ('b' == i)
            {
                st.push(i);
            }
            else if (!st.empty())
            {
                st.pop();
                ans++;
            }
        }
        return ans;
    }
};

class Solution {
public:
    int minimumDeletions(string s) {
        // 前缀和解法
        int n = s.length();
        vector<int> sumA(n + 1);
        vector<int> sumB(n + 1);
        for (int i = 0; i < n; ++i) 
        {
            sumA[i + 1] = sumA[i] + (s[i] == 'a');
            sumB[i + 1] = sumB[i] + (s[i] == 'b');
        }
        int ans =  sumA[n];//得到所有的a值
        for (int i = 1; i <= n; ++i) {
            //逐步比较删a,还是删b
            ans = min(ans, sumB[i] + sumA[n] - sumA[i]);
        }
        return ans;
    }
};
//2022 0306

悦读

道可道，非常道；名可名，非常名。 无名，天地之始，有名，万物之母。 故常无欲，以观其妙，常有欲，以观其徼。 此两者，同出而异名，同谓之玄，玄之又玄，众妙之门。

最新收录
【已解决】“you should not run configure as root (set FORCE_UNSAFE_CONFIGURE=1 in environment）
基于springboot 的图书管理系统
首先，定义一个时钟类——Clock，它包括三个int型 成员变量分别表示时、分、秒，一个构造方法用于对三个成员变量（时、分、秒） 进行初始化，还有一个成员方法show()用于显示时钟对象的时间。其次，...
J1019基于SpringBoot的护肤品推荐系统设计与实现（源码+包运行+技术指导）
计算机毕业设计JAVA旅行社网站系统mybatis+源码+调试部署+系统+数据库+lw
Linux cron定时任务常用方法
HDU - 2057 (纯C语言模拟16进制加减法)
一个技能表
ES6算法---快速排序 Quicksort
ip地址、子网掩码、网段、子网划分
;