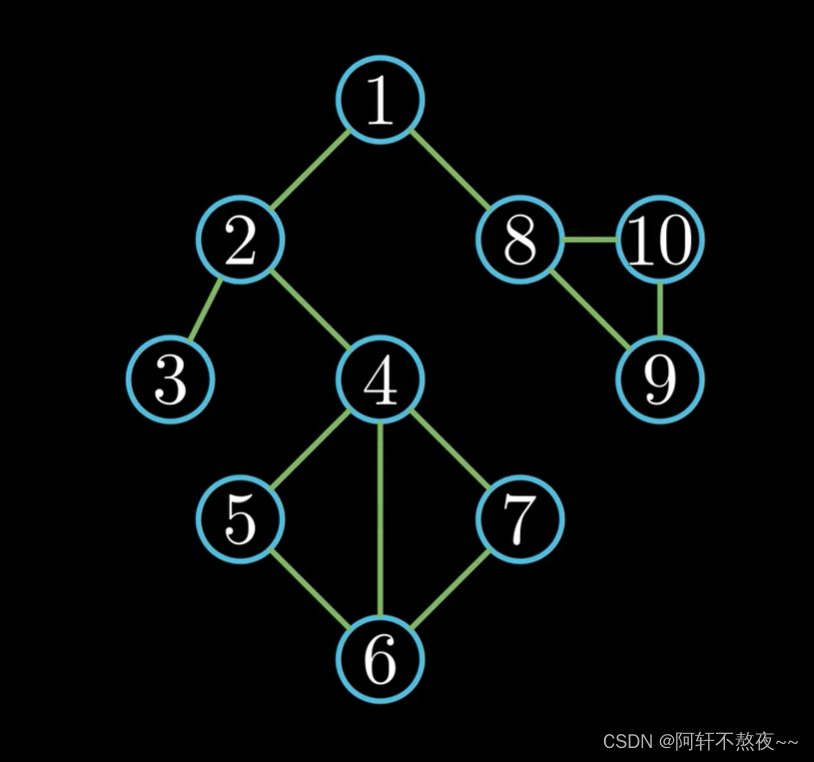
一.dfs算法的介绍。
深度优先搜索算法(Depth First Search,简称DFS):一种用于遍历或搜索树或图的算法。 沿着树的深度遍历树的节点,尽可能深的搜索树的分支。当节点v的所在边都己被探寻过或者在搜寻时结点不满足条件,搜索将回溯到发现节点v的那条边的起始节点。整个进程反复进行直到所有节点都被访问为止。属于盲目搜索,最糟糕的情况算法时间复杂度为O(!n)。
(简单来说就是一条路走到黑,直到走不动,再回头继续走,直到搜索完全部为止)
过程图如下:
深度优先搜索,以深度为优先选项,它会走遍所有的路径,即枚举所有完整路径来找到最佳的路径。
二.例题分析。
一.迷宫问题。
对于迷宫问题属于非常经典的dfs例题,其解决思路很符合dfs搜索过程。
https://www.luogu.com.cn/problem/P1605
题目描述
给定一个 N×M 方格的迷宫,迷宫里有 T 处障碍,障碍处不可通过。
在迷宫中移动有上下左右四种方式,每次只能移动一个方格。数据保证起点上没有障碍。
给定起点坐标和终点坐标,每个方格最多经过一次,问有多少种从起点坐标到终点坐标的方案。
输入格式
第一行为三个正整数 N,M,T,分别表示迷宫的长宽和障碍总数。
第二行为四个正整数 SX,SY,FX,FY,SX,SY 代表起点坐标,FX,FY 代表终点坐标。
接下来 T 行,每行两个正整数,表示障碍点的坐标。
输出格式
输出从起点坐标到终点坐标的方案总数。
输入输出样例
输入 #1复制
2 2 1 1 1 2 2 1 2
输出 #1复制
1
说明/提示
对于 100%100% 的数据,1≤N,M≤5,1≤T≤10,1≤SX,FX≤n,1≤SY,FY≤m。
解决思路
对于本题没有太多的难点,就是dfs基本的解题思路。
定义二维数组a和book,分别用于存放地图和标记数组。
开一个方向数组,方便搜索
int next[4][2]={{0,1},{1,0},{0,-1},{-1,0}};边界条件
if(fx<1||fx>n||fy<1||fy>m)
continue;核心代码
for(int i=0;i<4;i++)
{
fx=x+next[i][0];
fy=y+next[i][1];
if(fx<1||fx>n||fy<1||fy>m)
continue;
if(book[fx][fy]==0&&a[fx][fy]==0)
{
book[fx][fy]=1;
dfs(fx,fy);
book[fx][fy]=0;
}
}完整代码
#include<stdio.h>
int n,m,x1,y1,x2,y2,num=0;
int h,g;
int a[10][10]; //存储地图
int book[10][10]={0}; //标记作用
void dfs(int x,int y)
{
int fx,fy;
int next[4][2]={{0,1},{1,0},{0,-1},{-1,0}}; //方向数组
if(x==x2&&y==y2) //结束条件
{
num++;
return ;
}
for(int i=0;i<4;i++)
{
fx=x+next[i][0];
fy=y+next[i][1];
if(fx<1||fx>n||fy<1||fy>m) //边界条件
continue;
if(book[fx][fy]==0&&a[fx][fy]==0)
{
book[fx][fy]=1; //标记
dfs(fx,fy);
book[fx][fy]=0; //回溯
}
}
}
int main()
{
scanf("%d%d",&n,&m);
int k;
scanf("%d",&k);
scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
for(int i=0;i<k;i++)
{
scanf("%d%d",&h,&g);
a[h][g]=1;
}
book[x1][y1]=1;
dfs(x1,y1);
printf("%d\n",num);
return 0;
}二.填涂颜色。
本题就可以通过dfs解决又可以通过bfs解决,此处就dfs方法进行分析。
https://www.luogu.com.cn/problem/P1162
题目描述
由数字 0 组成的方阵中,有一任意形状的由数字 1 构成的闭合圈。现要求把闭合圈内的所有空间都填写成 2。例如:6×6 的方阵(n=6),涂色前和涂色后的方阵如下:
如果从某个 0 出发,只向上下左右 4 个方向移动且仅经过其他 00的情况下,无法到达方阵的边界,就认为这个 0 在闭合圈内。闭合圈不一定是环形的,可以是任意形状,但保证闭合圈内的 0 是连通的(两两之间可以相互到达)。
0 0 0 0 0 0
0 0 0 1 1 1
0 1 1 0 0 1
1 1 0 0 0 1
1 0 0 1 0 1
1 1 1 1 1 1
0 0 0 0 0 0
0 0 0 1 1 1
0 1 1 2 2 1
1 1 2 2 2 1
1 2 2 1 2 1
1 1 1 1 1 1
输入格式
每组测试数据第一行一个整数 n(1≤n≤30)。
接下来 n 行,由 0 和 1 组成的 n×n 的方阵。
方阵内只有一个闭合圈,圈内至少有一个0。
输出格式
已经填好数字 2 的完整方阵。
输入输出样例
输入 #1复制
6 0 0 0 0 0 0 0 0 1 1 1 1 0 1 1 0 0 1 1 1 0 0 0 1 1 0 0 0 0 1 1 1 1 1 1 1
输出 #1复制
0 0 0 0 0 0 0 0 1 1 1 1 0 1 1 2 2 1 1 1 2 2 2 1 1 2 2 2 2 1 1 1 1 1 1 1
说明/提示
对于 100%100% 的数据,1≤n≤30。
解题思路
题目要求我们将被1围住的空间中的0全部改为2,但是直接按照这样写显得繁琐,那我们不妨逆向思维,将外面的0全部改为2,那么剩余为0的不就应该是被围起来的空间。最后我们们将0全部改为2,将3再改回0,输出地图就ok了。
思路理完代码就非常容易了。
这里有一个小技巧,我们可以将数组开的大比地图大一点,地图从(1,1)开始录入,这样就可以一搜到底了,不需要遍历地图,这样简化我们的过程。
过程就不多赘述了,直接上代码
完整代码
#include<stdio.h>
int n;
int a[100][100]={0};
int next1[4]={1,0,-1,0}; //方向数组
int next2[4]={0,1,0,-1};
void dfs(int x,int y)
{
a[x][y]=3;
int dx,dy;
for(int i=0;i<4;i++) //核心代码都一样,就不过多解释了
{
dx=x+next1[i];
dy=y+next2[i];
if(dx<0||dx>n+1||dy<0||dy>n+1)
continue;
if(a[dx][dy]==0)
{
dfs(dx,dy);
}
}
return;
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++) //从1开始录入地图
{
for(int j=1;j<=n;j++)
{
scanf("%d",&a[i][j]);
}
}
dfs(0,0); //直接从原点开始搜索
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
if(a[i][j]==0) //转换一下
a[i][j]=2;
if(a[i][j]==3)
a[i][j]=0;
}
}
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
printf("%d ",a[i][j]);
}
printf("\n");
}
return 0;
}三.八皇后 Checker Challenge。
https://www.luogu.com.cn/problem/P1219
最后我们来看一下比较复杂的八皇后问题,比较一下本题和前面两题的区别,总结经验。
题目描述
一个如下的 6×6 的跳棋棋盘,有六个棋子被放置在棋盘上,使得每行、每列有且只有一个,每条对角线(包括两条主对角线的所有平行线)上至多有一个棋子。
上面的布局可以用序列 2 4 6 1 3 5来描述,第 i 个数字表示在第 i 行的相应位置有一个棋子,如下:
行号 1 2 3 4 5 6
列号 2 4 6 1 3 5
这只是棋子放置的一个解。请编一个程序找出所有棋子放置的解。
并把它们以上面的序列方法输出,解按字典顺序排列。
请输出前 3 个解。最后一行是解的总个数。
输入格式
一行一个正整数 n,表示棋盘是n×n 大小的。
输出格式
前三行为前三个解,每个解的两个数字之间用一个空格隔开。第四行只有一个数字,表示解的总数。
输入输出样例
输入 #1复制
6
输出 #1复制
2 4 6 1 3 5 3 6 2 5 1 4 4 1 5 2 6 3 4
说明/提示
【数据范围】
对于 100%100% 的数据,6≤n≤13。
题目翻译来自NOCOW。
USACO Training Section 1.5
对于主体部分我们仍然可以套用上面的核心代码,根据题意,两个皇后不能出现在同一行,列,对角线上,首先我们要知道在同一个对角线上怎么表示。
上对角线(hang-lie)行号-列号 (hang-lie+7)都为正数。
下对角线(hang+lie)行号+列号
知道这个就好办多了,然后我们为了方便通过定义4个一维数组,hang,lie,shang,xia分别代表四条线,然后我们一行一行的遍历,这样就可以通过一维数组实现对整个棋盘的搜索。
最后完整代码附上
#include<stdio.h>
int hang[15],lie[15],shang[100],xia[100]; //三个一维数组用来标记,看是否被占用
int n,num=0;
void dfs(int x) //注意这里是一行一行的遍历
{
if(x>n) //遍历完棋盘
{
num++; //统计有多少中方法
if(num<=3) //输出前三个
{
for(int i=1;i<=n;i++)
printf("%d ",hang[i]); //数组hang用来存储皇后的位置
printf("\n");
}
return;
}
for(int i=1;i<=n;i++) //核心代码,只是增加了判断条件
{
if(lie[i]==0&&shang[x-i+7]==0&&xia[i+x]==0) //看是否被标记占用
{
hang[x]=i;
lie[i]=1;
shang[x-i+7]=1; //标记
xia[x+i]=1;
dfs(x+1);
lie[i]=0; //回溯
shang[x-i+7]=0;
xia[x+i]=0;
}
}
}
int main()
{
scanf("%d",&n);
dfs(1); //从第一行开始遍历数组
printf("%d\n",num);
return 0;
}三.总结。
对于dfs,可以用于多种情况,我们应合理的利用,在面对不同情景时,我们应该抓住核心,从多方面看待问题。dfs虽然可以解决很多问题,但求解过程相对暴力,在部分问题上不如bfs,以此,针对不同问题,找到适合的方法。
最后,这是目前我(新手小白)对于dfs一些粗陋的看法,其中肯定有一些错误,欢迎,接受批评建议,能够得到斧正。还是那句话,如果觉得错误过多,或者不认同,可以把这篇博客当做笑话。希望同大家一起进步!!!
如果dfs过程不明白的话可以看一下这篇博客
八皇后问题的详细题解可以看这一篇(有图,方便理解)