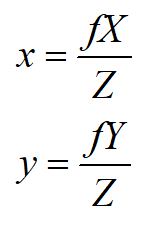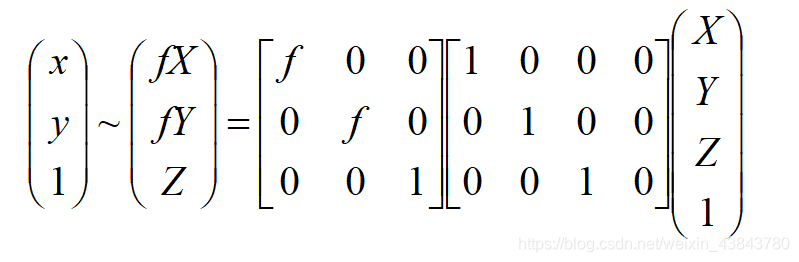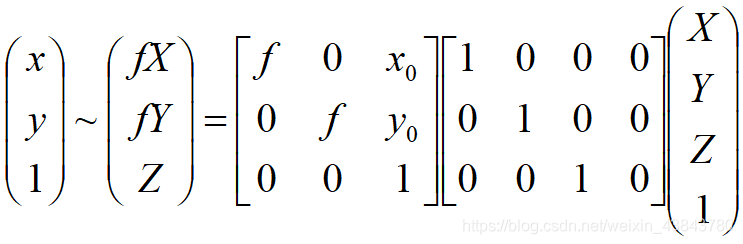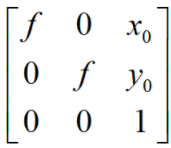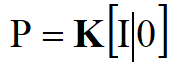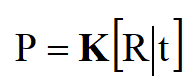相机标定的目的:获取摄像机的内参和外参矩阵(同时也会得到每一幅标定图像的选择和平移矩阵),内参和外参系数可以对之后相机拍摄的图像就进行矫正,得到畸变相对很小的图像。
摘自:https://blog.csdn.net/weixin_43843780/article/details/89294131
相机标定的原理及实现
邓程维 2019-04-14 11:16:41 23208 收藏 109
文章标签: 相机标定
版权
本文参考文档:
原理部分:https://blog.csdn.net/honyniu/article/details/51004397
代码部分:https://www.cnblogs.com/wildbloom/p/8320351.html ;https://blog.csdn.net/firemicrocosm/article/details/48594897#
1、相机标定的原理
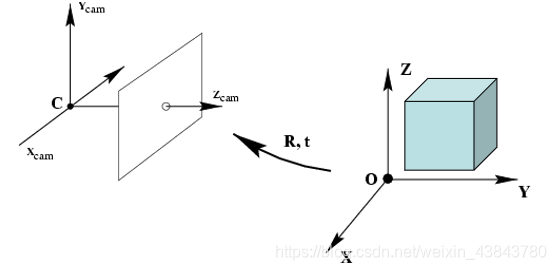
摄像机标定(Camera calibration)简单来说是从世界坐标系转换为相机坐标系,再由相机坐标系转换为图像坐标系的过程,也就是求最终的投影矩阵P的过程。
世界坐标系(world coordinate system):用户定义的三维世界的坐标系,为了描述目标物在真实世界里的位置而被引入。单位为m。
相机坐标系(camera coordinate system):在相机上建立的坐标系,为了从相机的角度描述物体位置而定义,作为沟通世界坐标系和图像/像素坐标系的中间一环。单位为m。
图像坐标系(image coordinate system):为了描述成像过程中物体从相机坐标系到图像坐标系的投影透射关系而引入,方便进一步得到像素坐标系下的坐标。 单位为m。
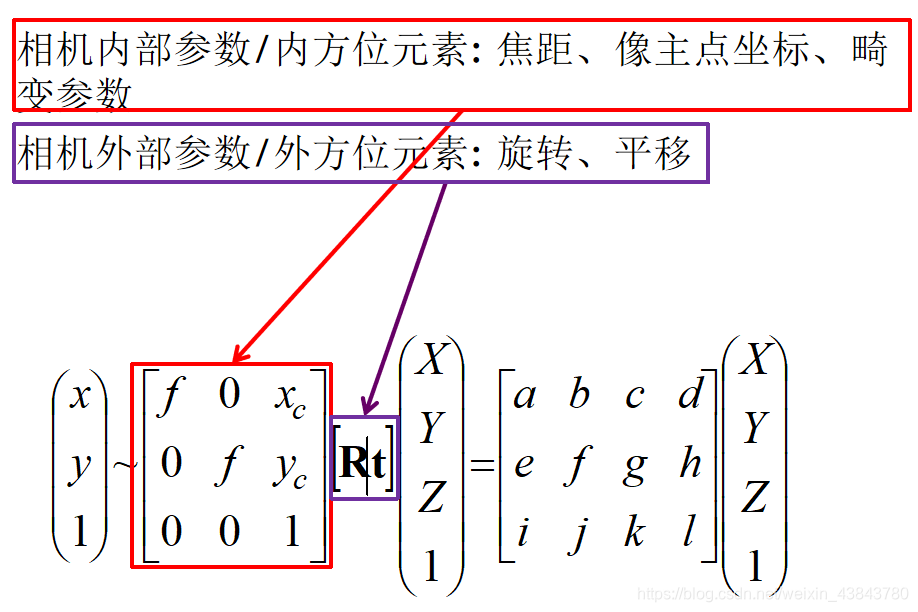
这一步是三维点到三维点的转换,包括R,t(相机外参)等参数;
这一步是三维点到二维点的转换,包括K(相机内参)等参数;
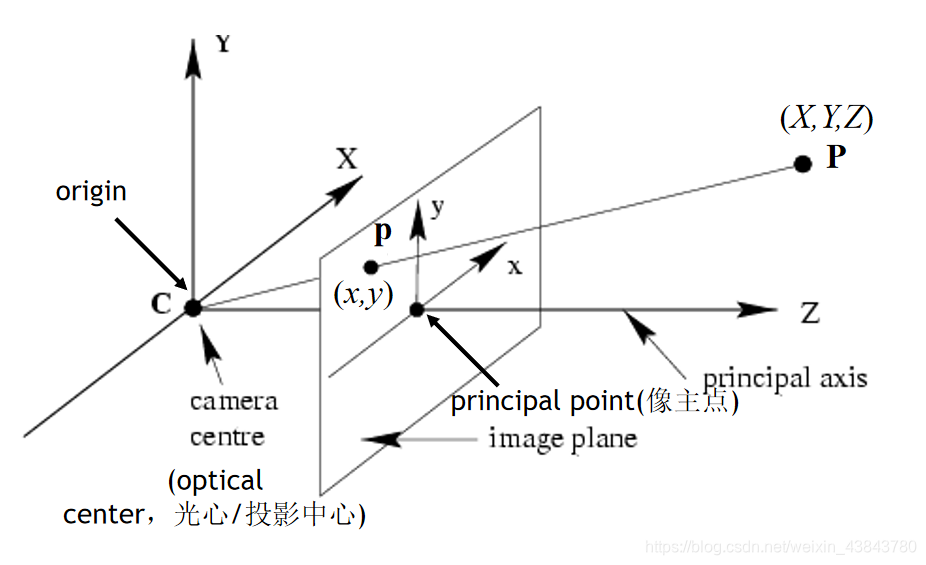
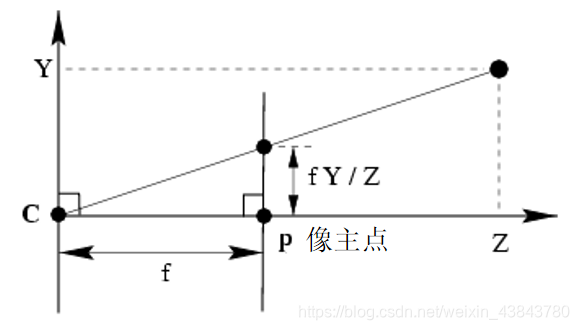
根据上述的关系图可以推导出下面的变换公式:
可以推出:
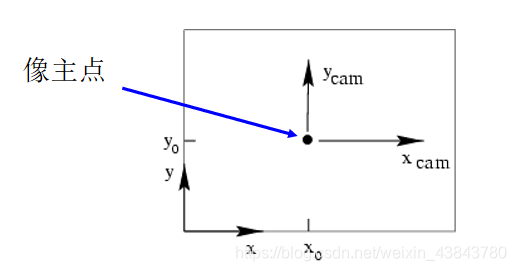
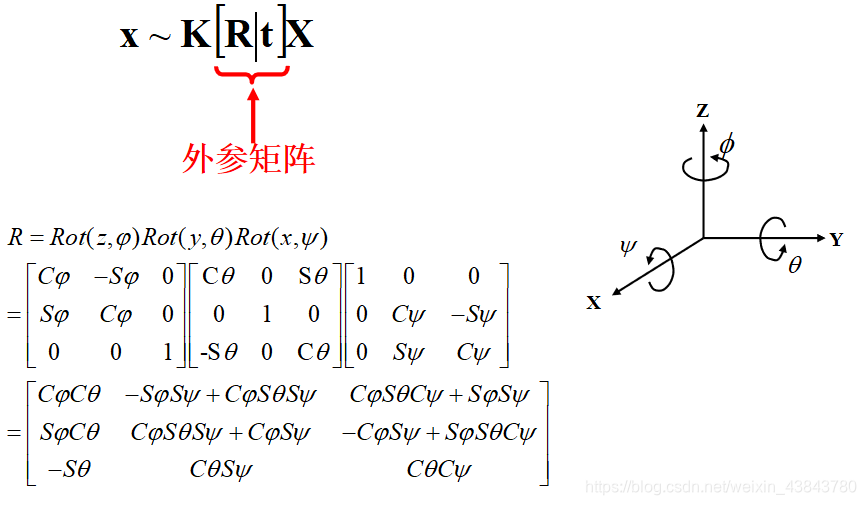
表示三个方向的偏转:
(在这里可以认为旋转矩阵 R 为单位矩阵 I,平移矩阵 t 都为0):
根据上述变换最终可以得到一个投影矩阵P的公式为:
总结一下公式大致如下:
在几何光学和阴极射线管显示中,畸变是对直线投影的一种偏移。简单来说直线投影是场景内的一条直线投影到图片上也保持为一条直线。那畸变简单来说就是一条直线投影到图片上不能保持为一条直线了,这是一种光学畸变。畸变一般可以分为两大类,包括径向畸变和切向畸变。主要的一般径向畸变有时也会有轻微的切向畸变。
2、相机标定的实现
相机标定的目的:获取摄像机的内参和外参矩阵(同时也会得到每一幅标定图像的选择和平移矩阵),内参和外参系数可以对之后相机拍摄的图像就进行矫正,得到畸变相对很小的图像。
相机标定的输入:标定图像上所有内角点的图像坐标,标定板图像上所有内角点的空间三维坐标(一般情况下假定图像位于Z=0平面上)。
相机标定的输出:摄像机的内参、外参系数。
这三个基础的问题就决定了使用Opencv实现张正友法标定相机的标定流程、标定结果评价以及使用标定结果矫正原始图像的完整流程:
- 准备标定图片
- 对每一张标定图片,提取角点信息
- 对每一张标定图片,进一步提取亚像素角点信息
- 在棋盘标定图上绘制找到的内角点(非必须,仅为了显示)
- 相机标定
- 对标定结果进行评价
- 查看标定效果——利用标定结果对棋盘图进行矫正
我准备的是下图这种格子数为7×5,内角点为6×4的棋盘格图片,手机型号为荣耀PLAY。
将它放在一个平面上从不同角度拍摄10张照片作为实验素材。
代码如下:
import cv2
import numpy as np
import glob
# 设置寻找亚像素角点的参数,采用的停止准则是最大循环次数30和最大误差容限0.001
criteria = (cv2.TERM_CRITERIA_MAX_ITER | cv2.TERM_CRITERIA_EPS, 30, 0.001)
# 获取标定板角点的位置
objp = np.zeros((4 * 6, 3), np.float32)
objp[:, :2] = np.mgrid[0:6, 0:4].T.reshape(-1, 2) # 将世界坐标系建在标定板上,所有点的Z坐标全部为0,所以只需要赋值x和y
obj_points = [] # 存储3D点
img_points = [] # 存储2D点
images = glob.glob("image4/*.jpg")
i=0;
for fname in images:
img = cv2.imread(fname)
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
size = gray.shape[::-1]
ret, corners = cv2.findChessboardCorners(gray, (6, 4), None)
#print(corners)
if ret:
obj_points.append(objp)
corners2 = cv2.cornerSubPix(gray, corners, (5, 5), (-1, -1), criteria) # 在原角点的基础上寻找亚像素角点
#print(corners2)
if [corners2]:
img_points.append(corners2)
else:
img_points.append(corners)
cv2.drawChessboardCorners(img, (6, 4), corners, ret) # 记住,OpenCV的绘制函数一般无返回值
i+=1;
cv2.imwrite('conimg'+str(i)+'.jpg', img)
cv2.waitKey(1500)
print(len(img_points))
cv2.destroyAllWindows()
# 标定
ret, mtx, dist, rvecs, tvecs = cv2.calibrateCamera(obj_points, img_points, size, None, None)
print("ret:", ret)
print("mtx:\n", mtx) # 内参数矩阵
print("dist:\n", dist) # 畸变系数 distortion cofficients = (k_1,k_2,p_1,p_2,k_3)
print("rvecs:\n", rvecs) # 旋转向量 # 外参数
print("tvecs:\n", tvecs ) # 平移向量 # 外参数
print("-----------------------------------------------------")
img = cv2.imread(images[2])
h, w = img.shape[:2]
newcameramtx, roi = cv2.getOptimalNewCameraMatrix(mtx,dist,(w,h),1,(w,h))#显示更大范围的图片(正常重映射之后会删掉一部分图像)
print (newcameramtx)
print("------------------使用undistort函数-------------------")
dst = cv2.undistort(img,mtx,dist,None,newcameramtx)
x,y,w,h = roi
dst1 = dst[y:y+h,x:x+w]
cv2.imwrite('calibresult3.jpg', dst1)
print ("方法一:dst的大小为:", dst1.shape)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
代码中的9、10、21、35行中的角点数根据自己的棋盘格大小进行更改。
实验分为两步,第一步主要是对每张图片进行角点的提取,结果如下:
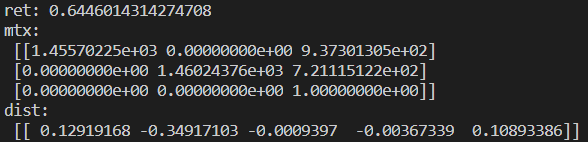
第二步就是实现相机的标定,运行结果如下:
mtx为内参数矩阵,dist为畸变系数:
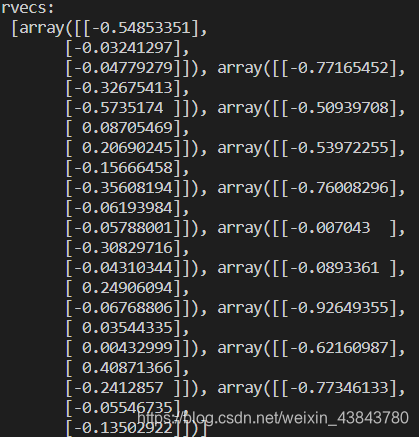
rvecs为旋转向量:
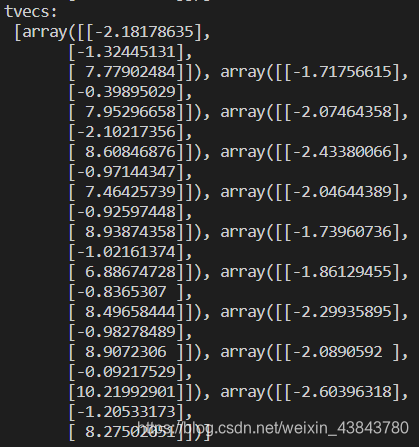
tvecs为平移向量:
畸变矫正:
矫正前后的图片
总结
通过标定得到荣耀PLAY的后置摄像头的内置参数矩阵为:
矫正后的图和原图通过对比发现差距并不大,只是在宽度上有一点拉伸(肉眼能看出的差距只有图片右上角的白字因为图片的拉伸而消失了),原因应该是原图基本上没有出现明显的畸变。(应该是现在的手机相机比较厉害吧…