分支定价算法Branch and price

分支定价算法是进阶版的列生成算法，是用来专门求解整数规划问题的。

列生成是求解线性规划问题的算法，通过不断往限制主问题中添加新列，最终将限制主问题变换为等价于原问题的形式。即原问题的最优基（A矩阵的基变量对应的a列）包含在最终的限制主问题中。但是列生成是求解线性规划问题的算法，对于整数规划问题不适用。为了弥补这个缺陷，采用分支的思想来予以解决，即通过分支来保留和筛选出最终等价于整数线性规划主问题的整数可行基。

可以这么理解，分支的操作+列生成=分支定价算法。因为列生成的子问题是定价子问题。

以下是具体的介绍。

1.整数规划与线性规划的关系

我们知道，列生成求解线性规划问题（LMP），最终得到的限制主问题（RLMP）的解等同于一开始的线性规划问题。即存在 $z_{LMP}^{*}=z_{RLMP}^{*}$ 。

此外，对于整数规划问题（MP）而言，它的解劣于松弛的线性规划问题（LMP）的解。即存在 $z_{MP}^{*}\geqslant z_{LMP}^{*}$ 。

合并上述两个不等式，即得到式1： $z_{MP}^{*}\geqslant z_{LMP}^{*}=z_{RLMP}^{*}$ 。

但是假如限制主问题（RLMP）的解为整数解，那么我们又可以得到限制主问题（RLMP）的整数解为原来整数规划问题的上界，即又有式2： $z_{MP}^{*}\leqslant z_{RLMP}^{*}$ 存在。

综上，汇总式1和式2，即有 $z_{MP}=z_{RLMP}^{*}$ 存在。

换句话说，假如限制主问题（RLMP）得到的解为整数解，那么我们就得到原来整数规划（MP）问题的最优解了。

那么问题就转化为如何使限制主问题（RLMP）求得整数解。

2.限制主问题（RLMP）求得整数解

分析限制主问题（RLMP）的单纯形表可知：假如解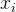 $x_{i}$ 存在非整数解，那么其对应的必定不会是整数最优对应的全部基（最优基）。因为假如是整数最优对应的最优基，那么解必定都是整数解。（注意：我们不能得到最优基是否包含该基，可能包含，也可能不包含。但一定能得到当前基一定不是最优基。）

基即列向量，最优基我们称为列池pool。

所以最终整数最优对应的最优基要么包含该基，要么不包含该基。按照这个思路进行分支。具体而言，分为两类：

（1）最优基列池中包含该列（保留），即无论后续如何变化，列池中始终包含该列，该列不被其它因素影响始终在列池中。

（2）最优基列池中不包含该列（删除），即无论后续如何变化，列池中始终不包含该列，该列为列池禁止。

3.B&P用法：以VRPTW为例

分支规则可以分为按照路径分支，或者按照弧分支。

按照路径分支，可能存在分支树不平衡的情况。因为左边始终添加约束，该路径必须被包含，即删除该路径服务的所有客户点（那么后续操作不会影响这条路径，即这条路径被保留）；但是右边被禁止的支，我们限制该条路径下次服务的客户点为原来客户数-1，即这条路径被删除。那么右边因为删除了客户点，问题的规模会变小。那么分支树，左边和右边的结构会不平衡。

鉴于路径分支的缺陷，常采用弧分支的策略。

参考资料：

065-线性规划（十一）：分支定价算法哔哩哔哩bilibili