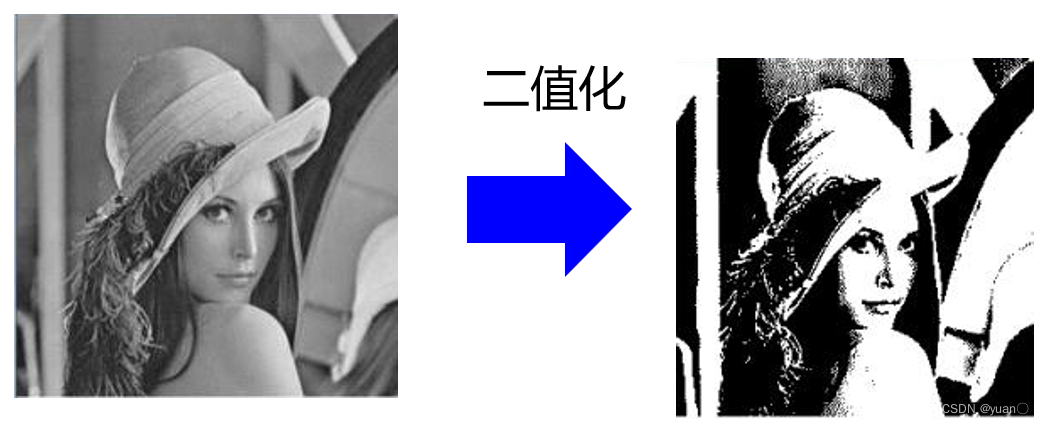
1. 二值化操作

    图像二值化定义：单通道图像$I$，对其任意像素值$I(x,y)$有:
$$\{\begin{array}{l}I(x,y)=255,ifI(x,y)>=Threshold,\\ I(x,y)=0,else.\end{array}$$    $Threshold$的设置，一般根据经验值或可动态设置。

    根据彩色图像的形成原理，一般的彩色图像都是由红色（Red）,绿色（Green），蓝色（Blue）三原色像素点按照一定的比例构成的RGB色彩空间图像。在OpenCV中，图像的色彩空间通常是BGR形式的，与一般情况下不同，所以需多加注意。如果需要对样品进行灰度化处理，就必须先用具体的色度值对每一种颜色进行参数的量化，以便区分。按照色度处理的惯例，通常将画面的色度值从0到255进行划分，一共包含了256个色度级别。其中，级别0和级别255分别代表了黑和白两种色彩。RGB图像数据的本质是一个三维整数矩阵，矩阵元素（0-255）。

    通过实验发现，当图像中的红色，绿色，蓝色三种像素点分别按照30%，59%，11%重新分配之后，能够得到与车道线灰度特征最为相近的灰度图。根据上述论调，可以得到RGB图像和灰度图像之间转换关系，为:$$X=0.30\ast R+0.59\ast G+0.11\ast B$$

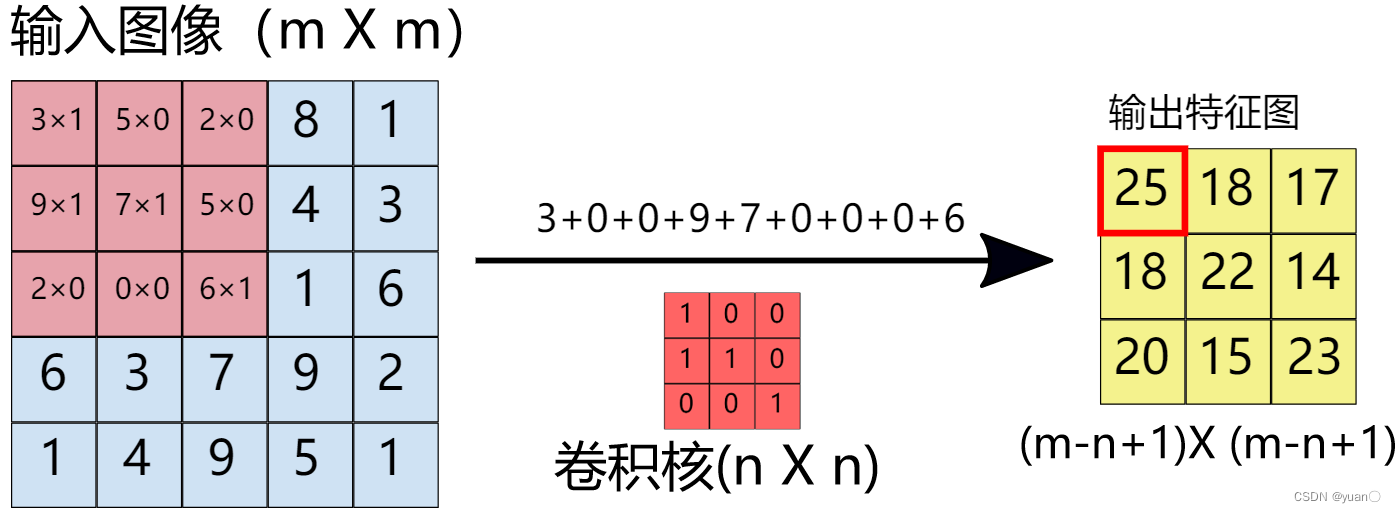
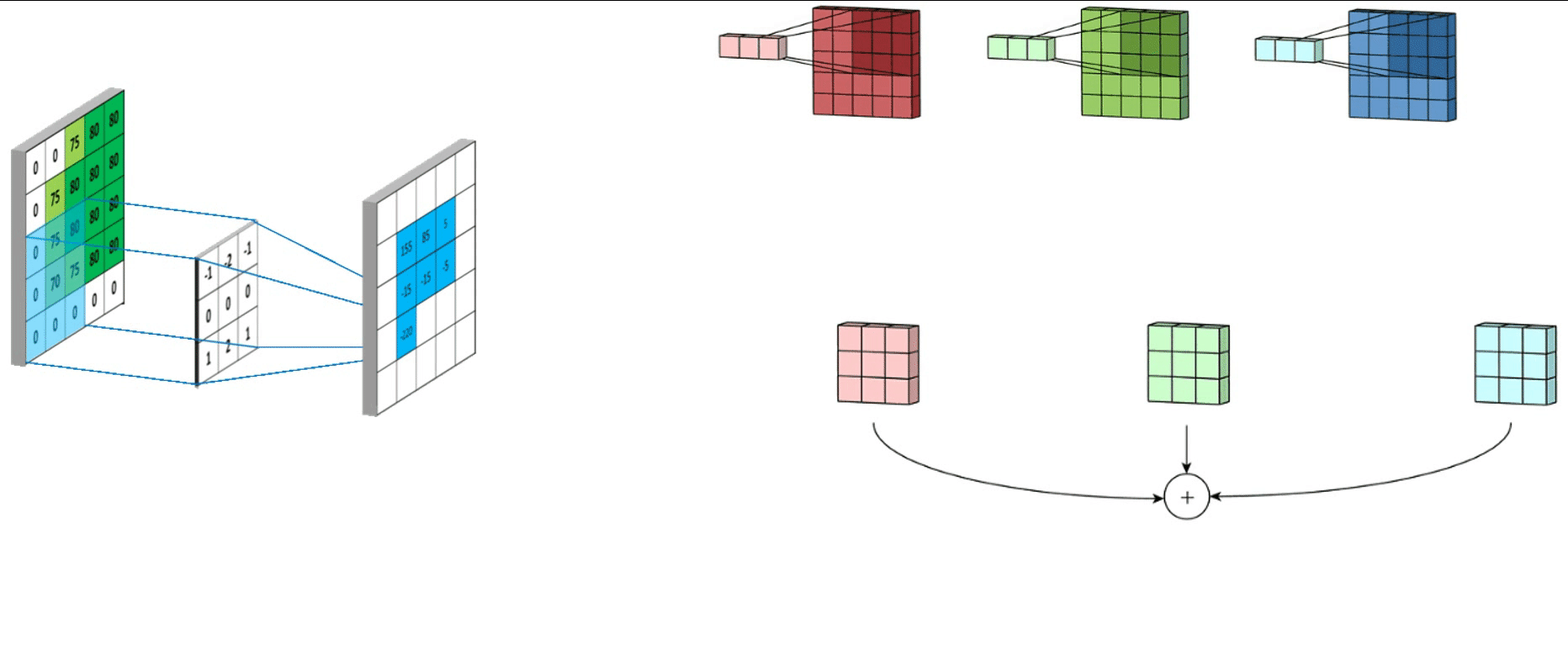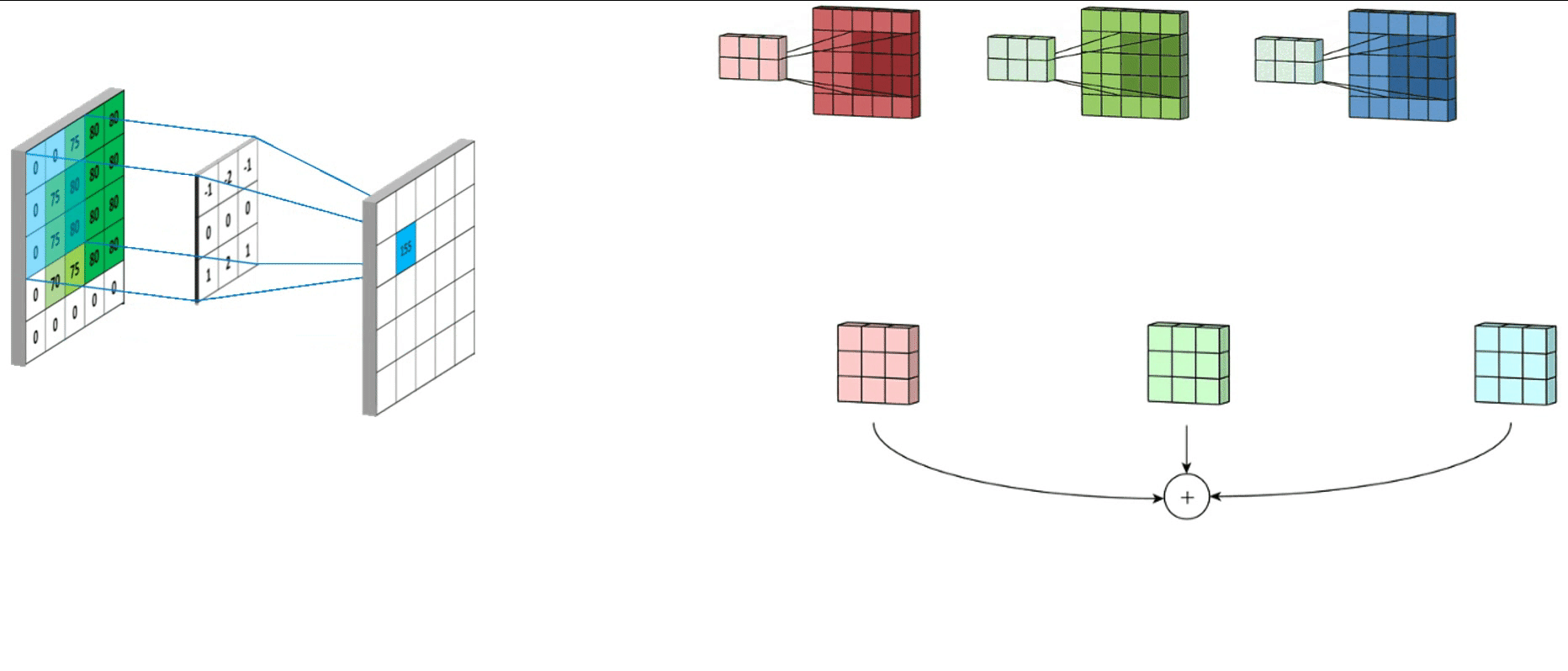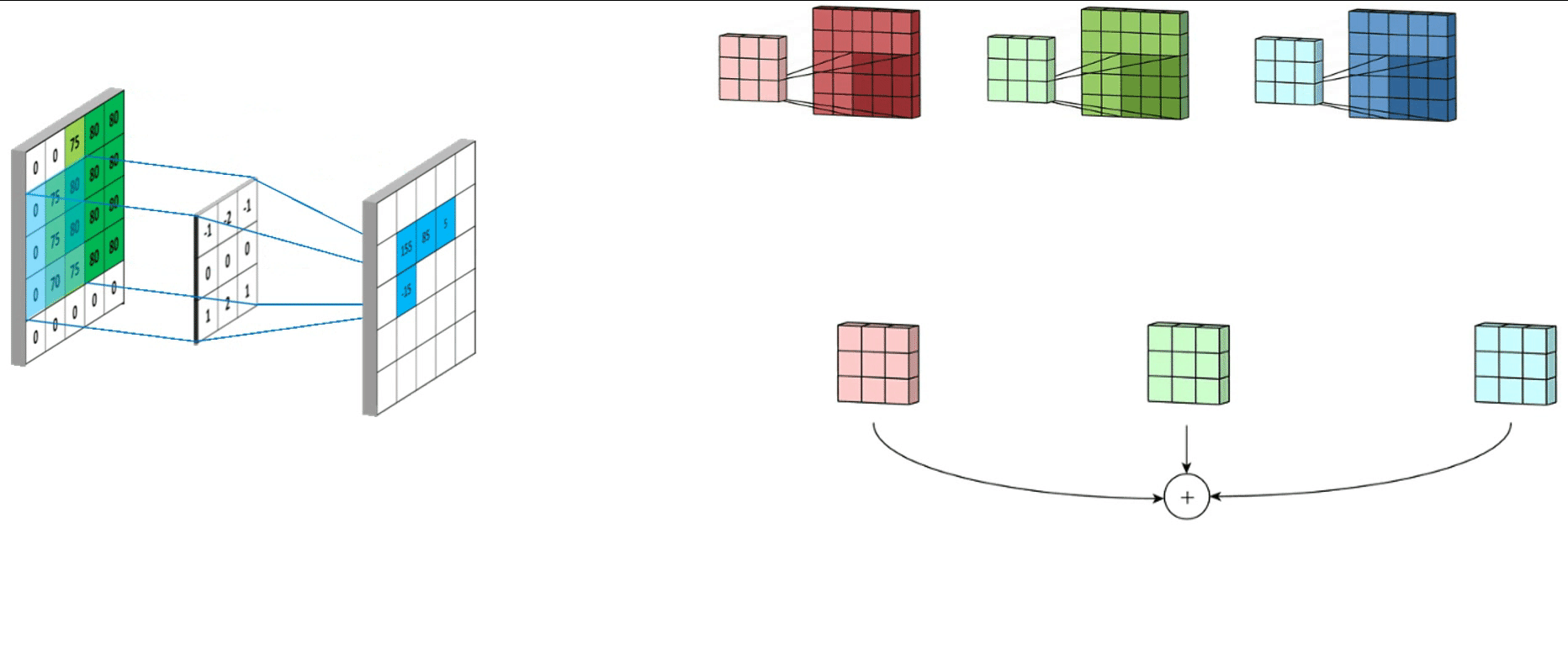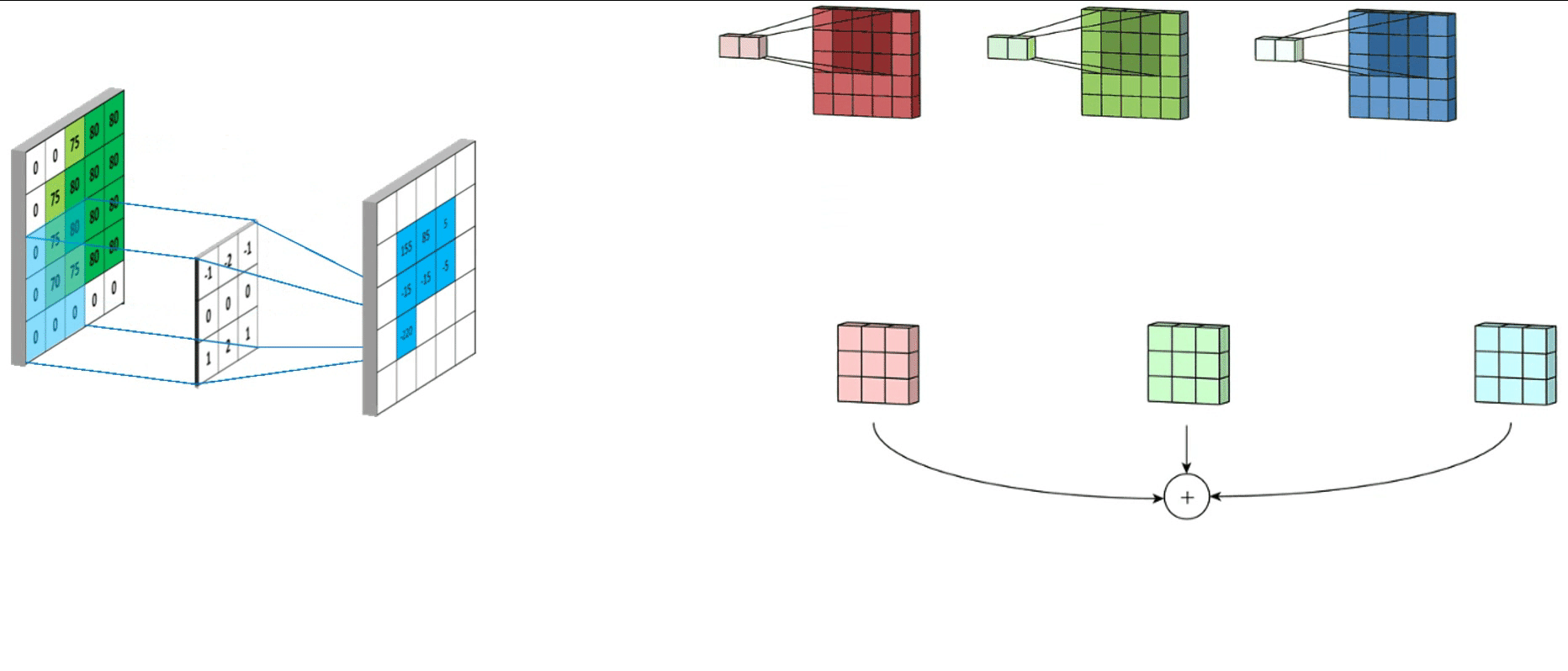
2. 卷积操作

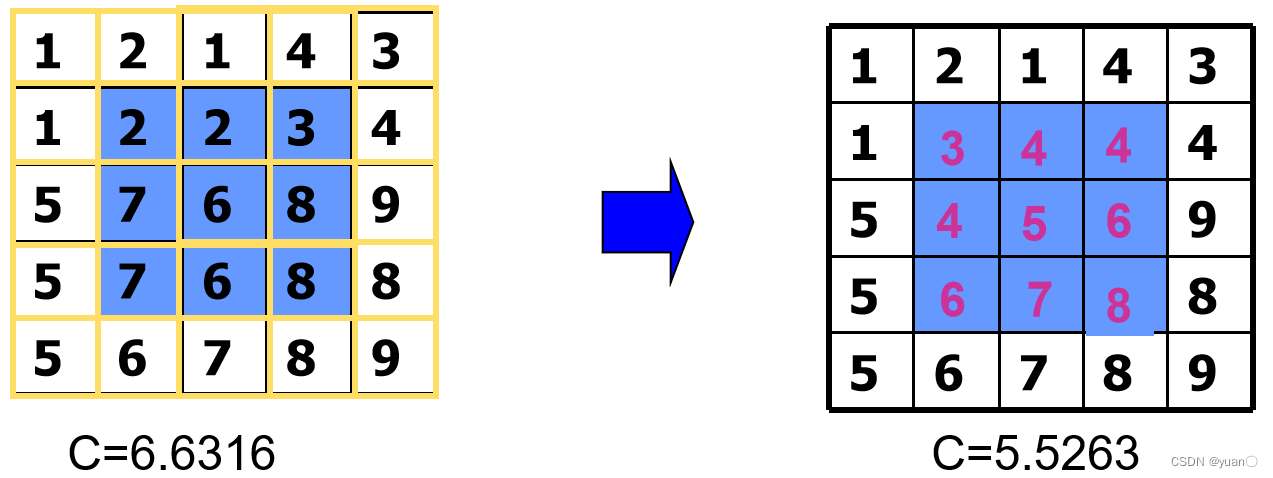
3. 均值滤波

    由归一化卷积框完成。用卷积框覆盖所有像素的平均值来代替中心元素。下式为3×3的归一化卷积框。$$K=\frac{1}{9}\left[\begin{array}{ccc}1& 1& 1\\ 1& 1& 1\\ 1& 1& 1\end{array}\right]$$

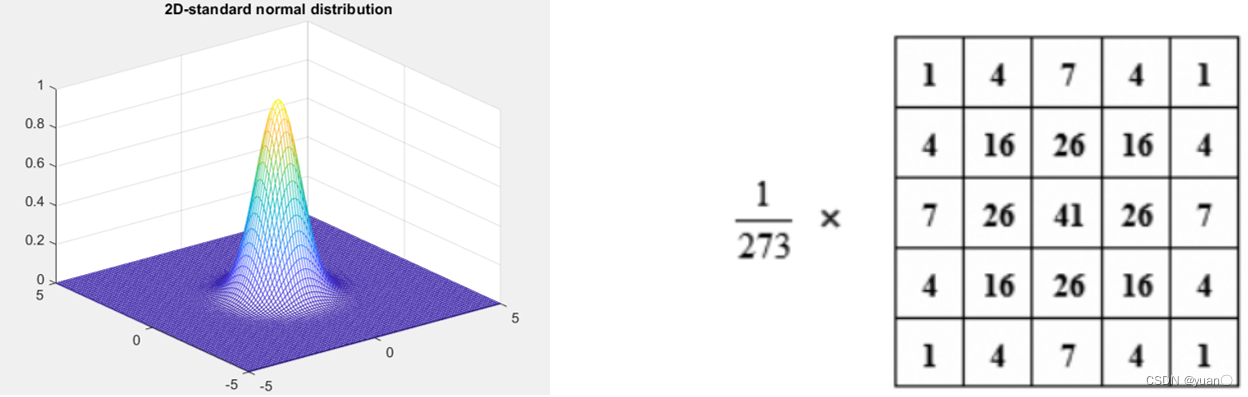
4. 高斯滤波

    采用了加权滤波平均的方式对图像进行去噪，减少随机性噪声的影响。卷积核的系数采用高斯分布,框中心的值最大，其余方框内的值根据与中心元素的距离递减，构成一个高斯“小山包”。高斯滤波可以有效从图像中去除高斯噪音。
    设定卷积核边长为$2n+1$时，像素$(u,v)$处的灰度按下式计算$$\begin{array}{l}{G}^{\prime }(u,v)=\sum _{j=-n}^n\sum _{i=-n}^{n}P(u+i,v+j)G(u+i,v+j)\\ P\tilde{N}((u,v),{\sigma }^2)\end{array}$$

5. 图像梯度算子

    定义：图像函数$f(x,y)$在点$(x,y)$的梯度是一个具有大小和方向的矢量，设为$G_x$ 和 $G_y$ 分别表示$x$方向和$y$方向的梯度，这个梯度的矢量可以表示为：$$G=[G_x,G_y]$$    梯度以及梯度的方向：$$\begin{array}{c}Edge\_Gradient(G)=\sqrt{G_x^2+G_y^2}\\ Angle(\theta )={\tan }^{-1}(\frac{G_x}{G_y})\end{array}$$

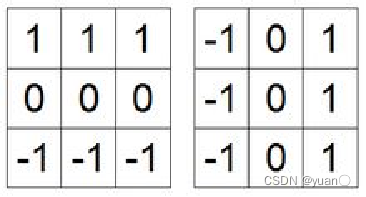
5.1 Prewitt梯度算子

特点：Prewitt算子利用像素点上下、左右邻点的灰度差

    Prewitt算子是一种一阶微分算子的边缘检测，利用像素点上下、左右邻点的灰度差，在边缘处达到极值检测边缘，去掉部分伪边缘，对噪声具有平滑作用 。其原理是在图像空间利用两个方向模板与图像进行邻域卷积来完成的，这两个方向模板一个检测水平边缘，一个检测垂直边缘。

5.2 Sobel梯度算子

特点：Sobel算子认为与中心像素相邻的像素重要性更大
    在边缘检测中，常用的一种模板是Sobel 算子。Sobel 算子有两个，一个是检测水平边缘的 ；另一个是检测垂直边缘的 。与Prewitt算子相比，Sobel算子对于象素的位置的影响做了加权，可以降低边缘模糊程度，因此效果更好。

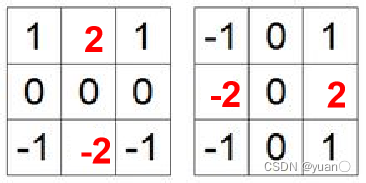
    Sobel算子是滤波算子的形式，用于提取边缘，可以利用快速卷积函数， 简单有效，因此应用广泛。美中不足的是，Sobel算子并没有将图像的主体与背景严格地区分开来，换言之就是Sobel算子没有基于图像灰度进行处理，由于Sobel算子没有严格地模拟人的视觉生理特征，所以提取的图像轮廓有时并不能令人满意。

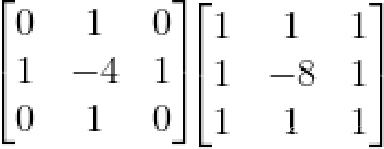
5.3 Laplace二阶梯度

特点：Laplace算子认为与二阶偏导也可以发现边缘，且旋转不变

    拉普拉斯算子（Laplace Operator）是n维欧几里德空间中的一个二阶微分算子，定义为梯度$（▽f）$的散度$（▽\cdot f）$。拉普拉斯算子也可以推广为定义在黎曼流形上的椭圆型算子，称为拉普拉斯-贝尔特拉米算子。

6. 边缘特征点提取算子

• 边缘是图像中的重要的结构性特征。
• 边缘往往存在于目标和背景之间，不同的区域之间。
• 图像边缘指的是那些附近像素点色度值普遍发生阶跃的地方，即梯度产生明显变化。

     Canny边缘检测是一种常见的边缘检测算法，其主要分为以下步骤：

1. 噪声去除：由于边缘检测很容易受到噪声的影响，常需要滤波器（高斯滤波等）进行降噪。
2. 计算图像梯度：对于平滑后的图像使用Sobel算子，计算出水平方向和竖直方向的一阶导数。根据梯度找到边界的梯度与方向。
3. 非极大值抑制：在获得梯度的方向和大小后，应对整个图像做一个扫描，去除那些非边界上的点。对每一个的进行扫描，看这个点的梯度是不是周围具有相同梯度方向的点中最大的，仅保留梯度大的边缘。
4. 滞后阈值（双阈值）：现在要确定那些边界才是真正的边界。这时我们需要设置两个阈值： minVal 和 maxVal 。当图像的灰度梯度高于 maxVal 时被认为是真的边界，那些低于 minVal 的边界会被抛弃。如果介于两者之间的话，就要看这个点是否与某个被确定为真正的边界点相连，如果是就认为它也是边界点，如果不是就抛弃。如下图所示。    A高于阈值 maxVal 所以是真正的边界点， C 虽然低于 maxVal但高于minVal 并且与 A 相连，所以也被认为是真正的边界点。而 B 就会被抛弃，因为他不仅低于 maxVal 而且不与真正的边界点相连。
       所以选择合适的 maxVal 和 minVal 对于能否得到好的结果非常重要。
       通过这一步的处理，一些小一点的噪声点也会被除去，因此我们假设边界都是长线段，以防止线段过短被当作噪点而除去。

7. 基于规则的特征点提取

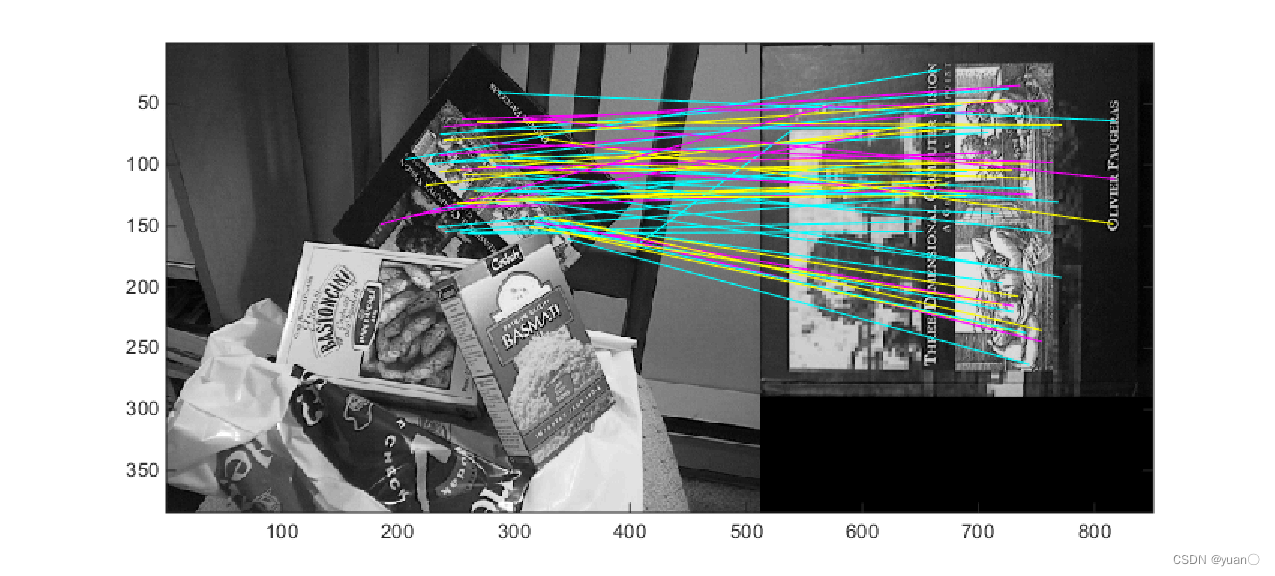
    SIFT（Scale-invariant feature transform）是一种检测局部特征的算法，可以提供对尺度和方向不敏感的特征描述子。
    SIFT第一步是寻找对尺度不敏感的待筛选特征点，接下来的步骤如下：
    SIFT将一个像素点周围比较大的区域（16x16）编码成一个高维的描述子，较单像素点具有更强的描述能力，方便去寻找两张图片中对应的特征点。
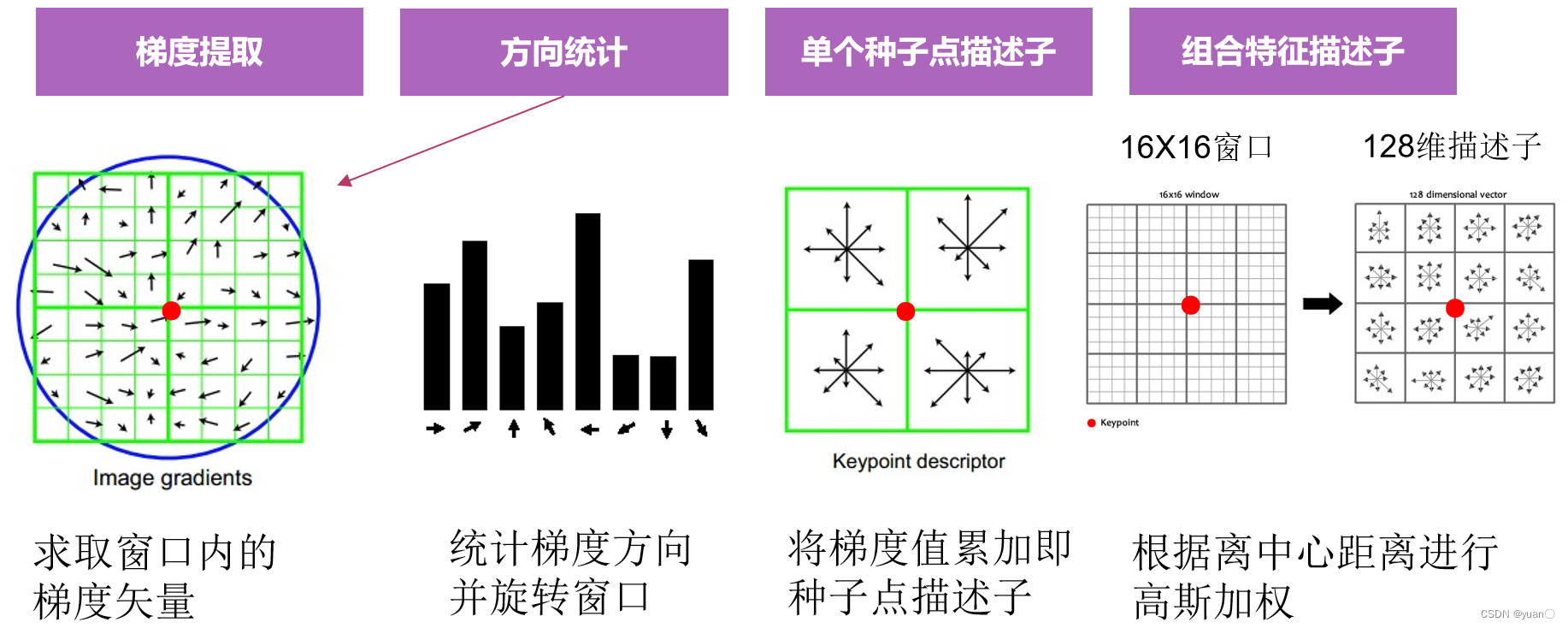
    用途：连续帧的处理，反求解运动关系，反求解空间关系。

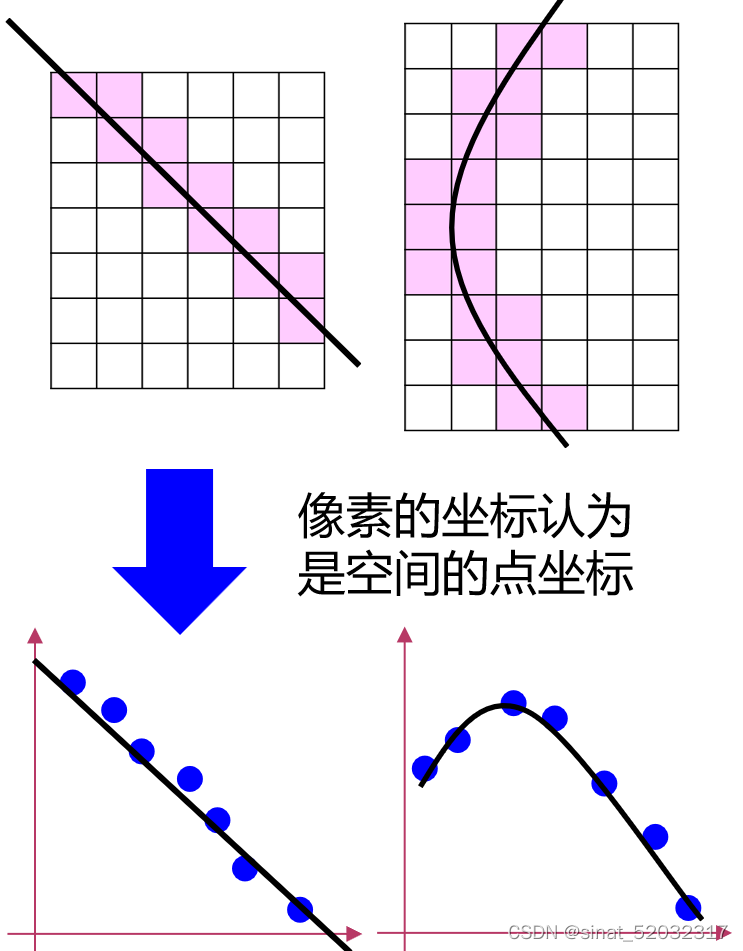
8. 最小二乘拟合方法

输入：二值图输出的属于车道线的$n$个像素点$I(x_i,y_i)=(u_i,v_i),i=(1,2,3,\dots .,n)$
输出：将像素拟合成的曲线（直线为例）

方法：曲线拟合问题，可采用最小二乘法求解，转换为参数估计问题。

1. 直线方程 $y=k\ast x+b，i=1,2,\dots ,n$
2. 定义优化函数
   $Minf（k,b）=sum((y_i–(k\ast x_i+b){)}^2),i=1,2,\dots ,n$
   求解此优化问题，可得$k，b$参数。

9. RANSAC曲线拟合

问题：最小二乘方法极容易受到数据中噪声的影响，对拟合的影响很大。
解决方法：鲁棒参数估计，如随机一致性采样方法（ RANSAC ）
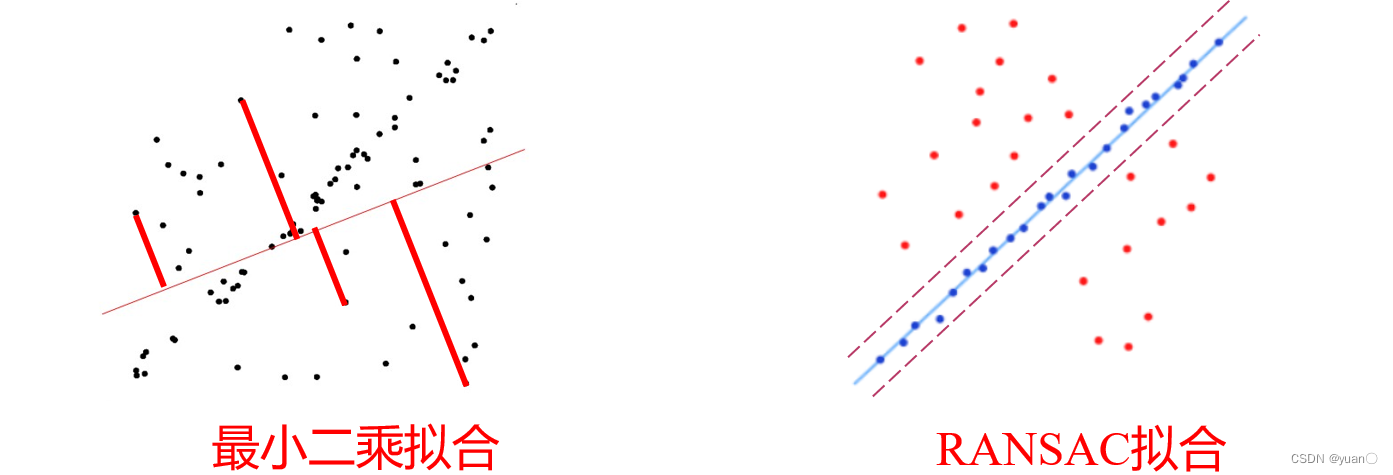
最小二乘拟合：最小化所有样本残差，使距离很远的噪点形成很大残差从而严重影响拟合效果
RANSAC拟合：尽可能使更多的样本位于拟合线附近误差范围内

10. Hough Transform 霍夫变换

霍夫变换是直线特征检测中常用的参数估计的方法
霍夫变换目的是在含有噪声的特征提取结果上拟合出直线
霍夫变换由Paul Hough在1962年提出，目的是找到图片中的直线.

     霍夫（Hough）变换是较为普遍使用的间断边缘连接方法的一种。霍夫变换的中心思想就是通过坐标系变换来检测直线，后来经过改进，可以检测椭圆。
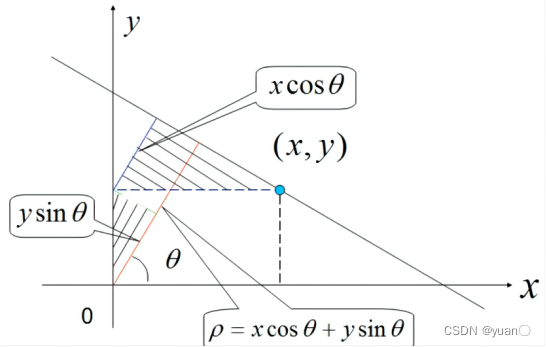
     在笛卡尔坐标系下，直线方程有点斜式、截距式等，以$y=kx+b$为例，很明显，此式难以表达垂直于$x$轴时直线的情况，而极坐标系则避免了此状况，通常情况下，极坐标系的表达式为$\rho =x\cos \theta +y\sin \theta$，直线在极坐标系下转换的图像如图所示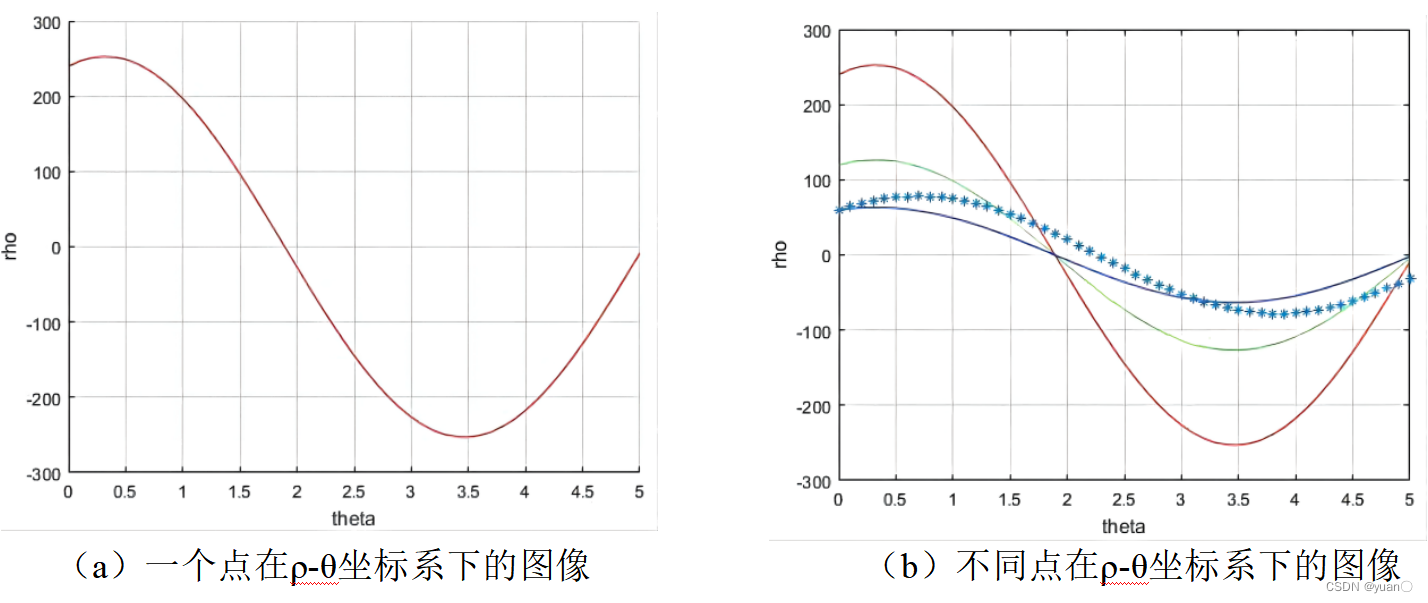：     如上图所示，笛卡尔坐标系中的任意一点在$\rho -\theta$坐标系下的图像为正弦曲线。图（b）中，红色、绿色以及蓝色曲线都为一条直线上的点，图像表明，同一直线上的不同点在$\rho -\theta$坐标系中会经过同一点。
     霍夫变换工作原理：
     每一条直线都可以用$（\rho ,\theta ）$表示。所以首先创建一个2维数组（累加器），初始化累加器，所有的值都为0。行表示$\rho$ ，列表示$\theta$。这个数组的大小决定了最后结果的准确性。如果希望角度精确到1度，就需要180列。对于$\rho$ ，最大值为图片对角线的距离。所以如果精确度要达到一个像素的级别，行数就应该与图像对角线的距离相等。对于图像空间内的直线，需对其每一个像素点进行极坐标转换，得到一系列关于$（\rho ,\theta ）$的数值对。每得到一对数值对$（\rho ,\theta ）$，便往累加器中相应的值加上1。遍历直线上所有的点，当遍历完时，找出累加器中最大值对应的数值队$（{\rho }_1,{\theta }_1）$。${\rho }_1$为该直线到原点的距离，${\theta }_1$为其垂线与横轴的夹角。

11. 基于学习的特征点提取

    基于学习的特征点提取本质也是卷积操作
    特征提取常用参数– 卷积核尺寸,即卷积核的宽度、高度大小。根据需求确定。常见为3x3，5x5，7x7.
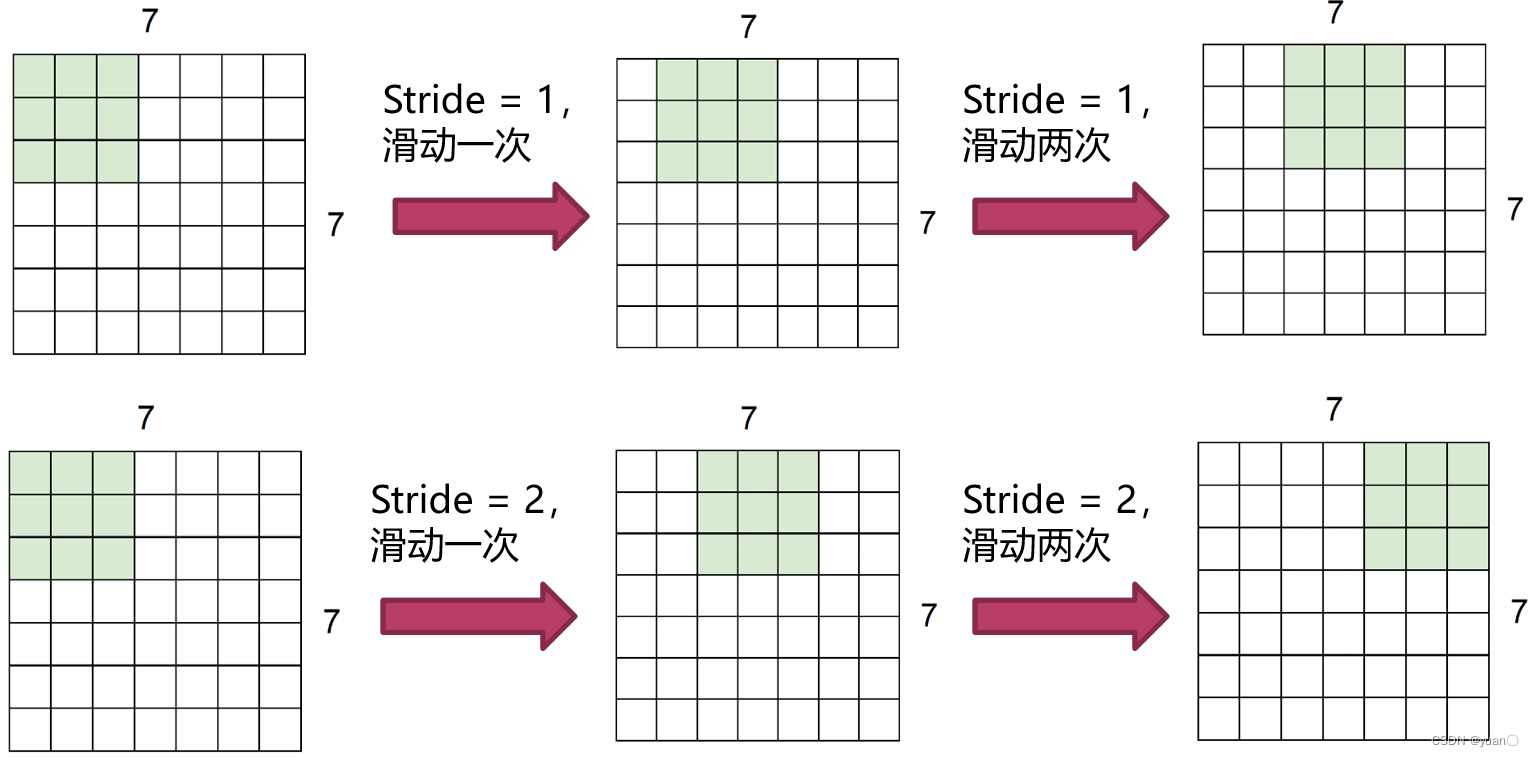
    特征提取常用参数- 步长,即卷积核滑动运算时，每步跳过的图像像素数.
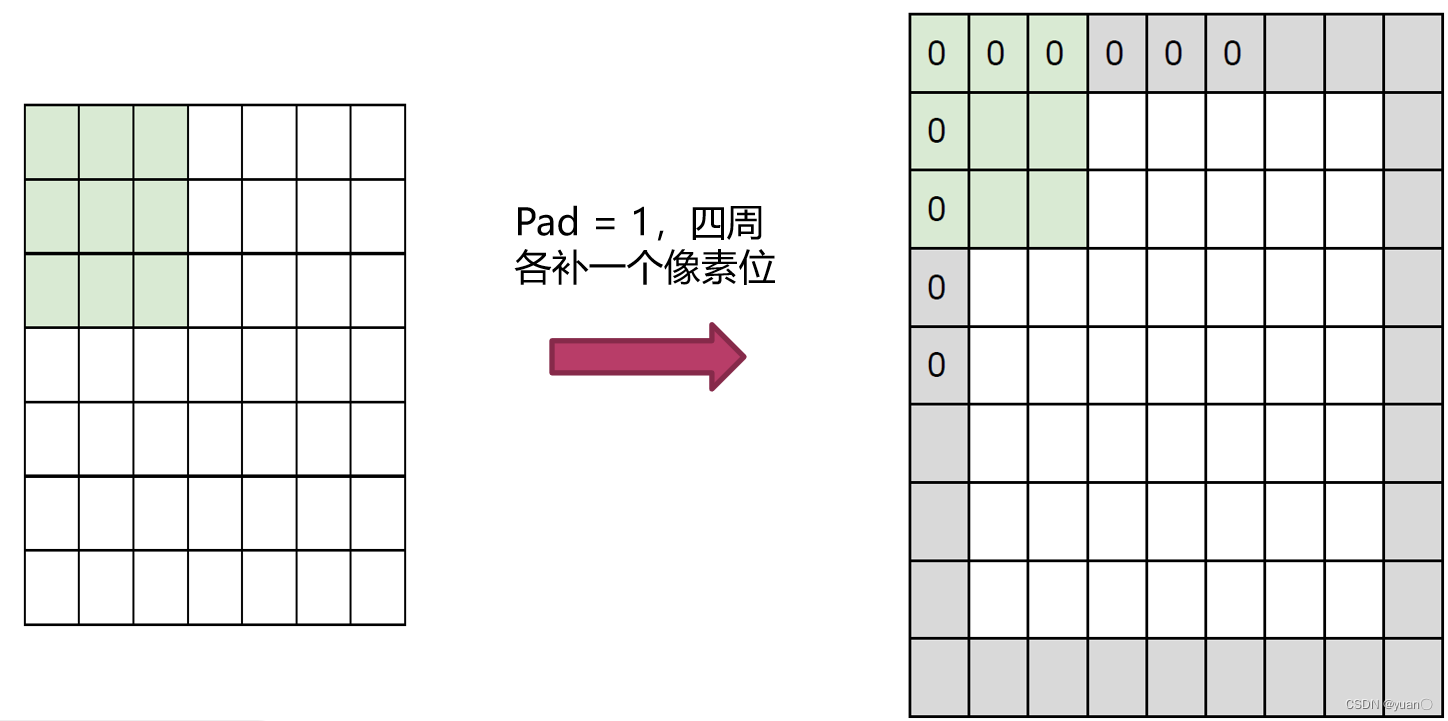
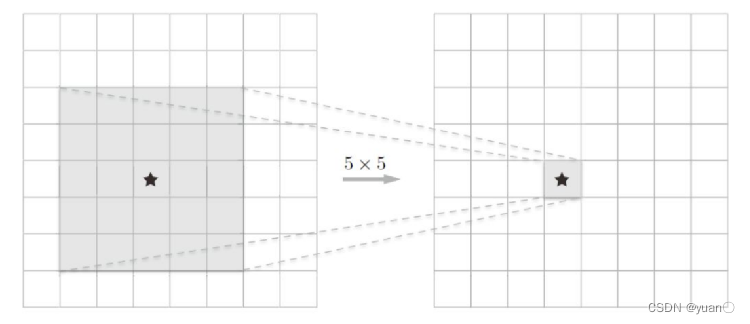
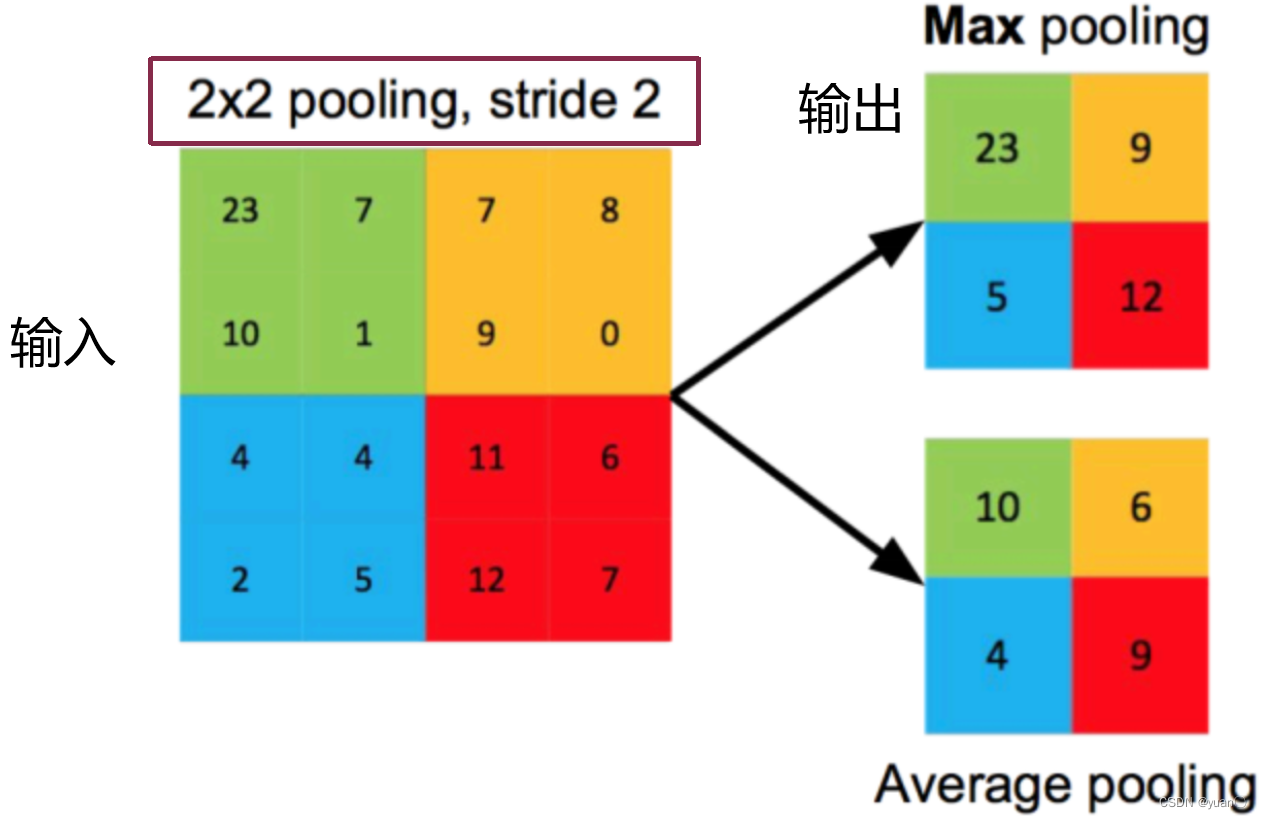
    特征提取常用参数– 补零位数,为便于卷积操作，有时会在输入图像四周补相应的像素（一般补充0像素），不改变卷积运算输出的情况下，适应卷积操作。    特征提取常用操作– 池化层（Pooling）

• 池化层作用一般用于减小特征图尺寸（降采样），凸显有用特征
• 可分为最大池化（Max Pooling和平均池化 Average Pooling）
• 池化层的参数为：池化核尺寸（Kernel Size），步长（Stride）
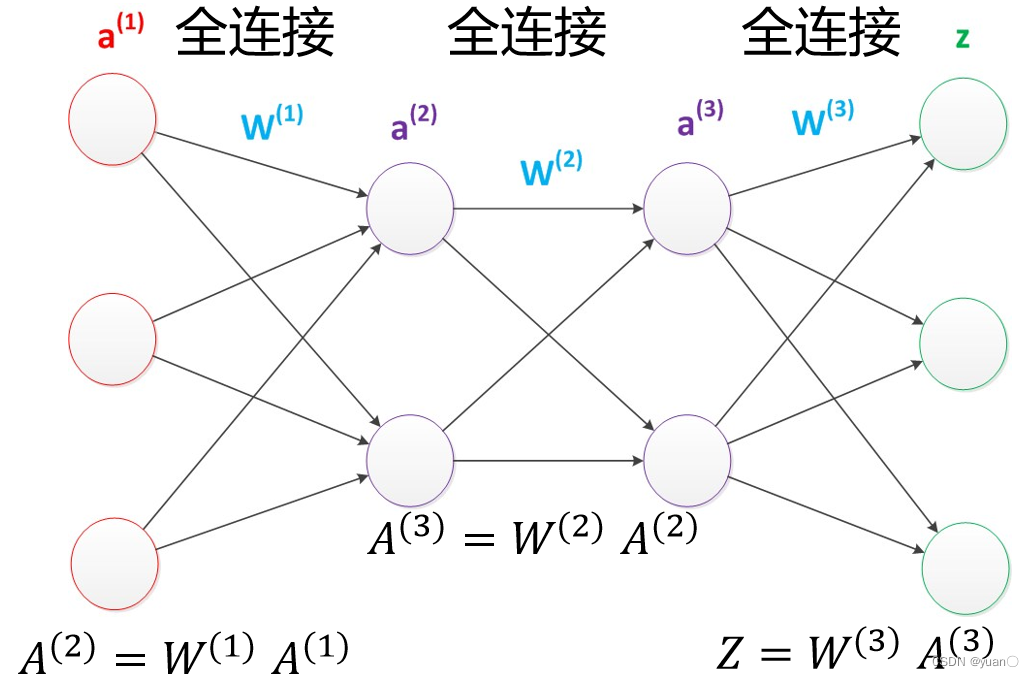
      特征空间变换 – 全连接层。全连接层的每一个结点都与上一层的所有结点相连，用来把前边提取到的特征综合起来。全连接的核心操作是矩阵乘法，本质上是把一个特征空间变换到另一个特征空间。

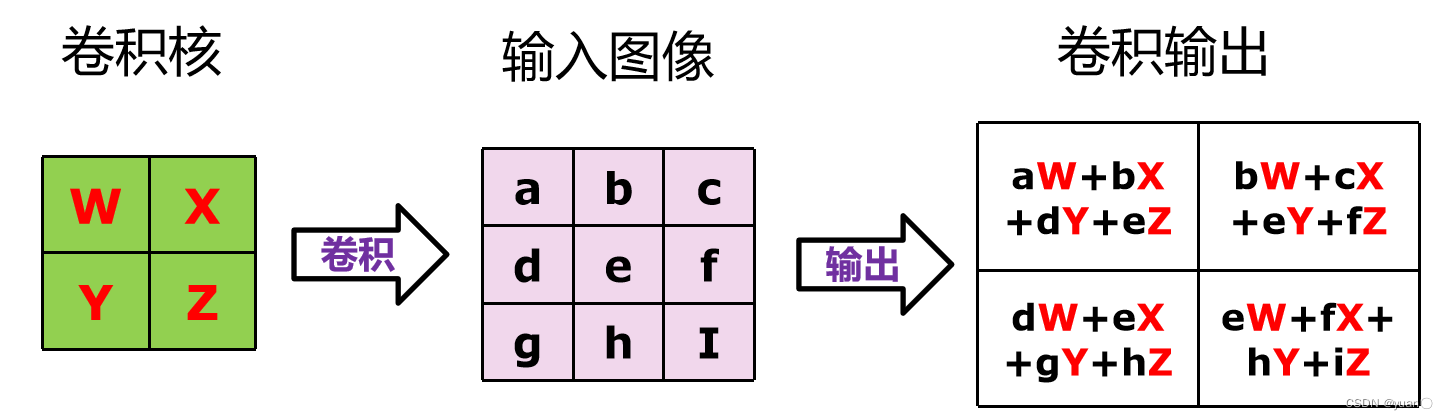
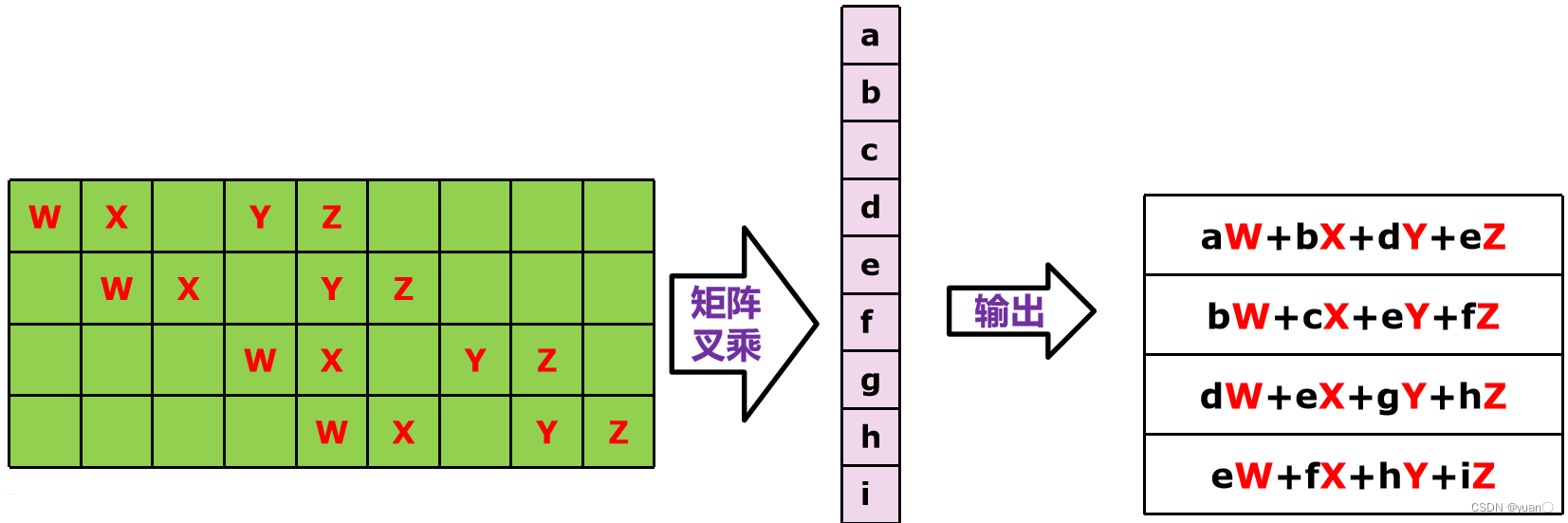
卷积运算类似于矩阵的叉乘。（稀疏矩阵的相乘）

图像矩阵的卷积可以等效为图像向量空间的线性变换

为什么深度学习网络可以提取信息？

• 网络中卷积核参数在监督学习中，不断去拟合，逼近某种提取。
• 参数调整好的网络，其本质是特征向量的空间变换+非线性组合。
  

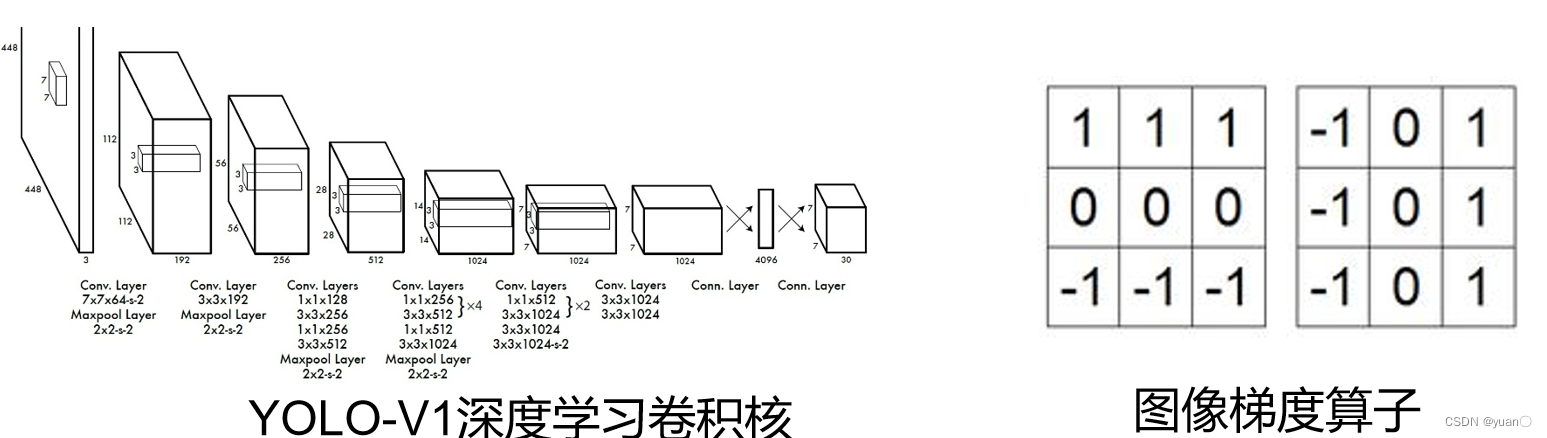
深度学习卷积核和梯度算子的卷积核有什么区别？

• 两种运算本质上都是一次矩阵相乘操作
• 区别是两种卷积核参数的来源不同（深度学习的卷积核参数是通过学习的方式获得的，图像梯度算子的卷积核参数是依据数学或物理人为定义的）

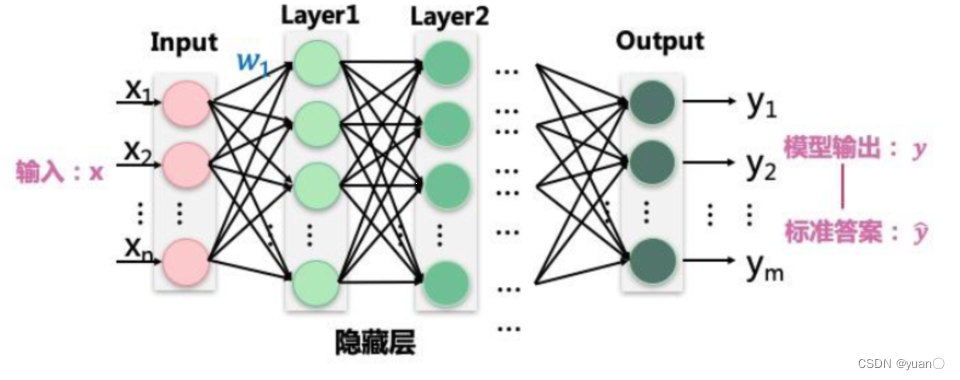
12. 神经网络的学习过程

卷积核里的参数怎么去拟合？
解决方法：神经网络，误差反向传播算法

• 计算模型输出与标准答案的误差反向调节隐藏层的参数
• 隐藏层的参数包含了卷积核的数值

题目汇总

正确项：
PS1：二值化方法适合提取黑色地面的白色车道线
PS2: Canny算子可以将过于细节的边缘滤除
PS3: Canny算子可以处理有高斯噪声的图片
PS4: SIFT特征在图片放大时具有一定的稳定性
PS5: 在窗口边缘处的种子描述子重要性相对较低
PS6: 最小二乘法会有过拟合问题
PS7: RANSAC需要知道拟合对象的模型
对于YOLO-V1：
其全连接层不是必须的，可以用卷积层替换
卷积核的参数是通过误差反向传播过程拟合的

错误项：
PS1: Canny算子提取的边缘比Sobel算子模糊
PS2: Canny算子认为梯度全局最大的点才是边缘点
PS3: SIFT特征没有利用梯度信息
PS4: SIFT特征的主方向仅由中心像素点的梯度决定
PS5: RANSAC只能拟合直线
PS6: 同一直线上的点霍夫变换后的直线相互平行

声明

本人所有文章仅作为自己的学习记录，若有侵权，联系立删。本系列文章主要参考了清华大学、北京理工大学、哈尔滨工业大学、深蓝学院、百度Apollo等相关课程。