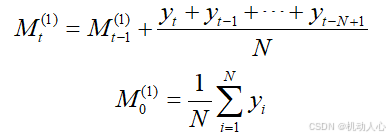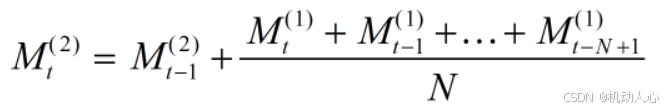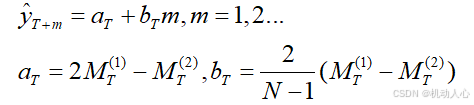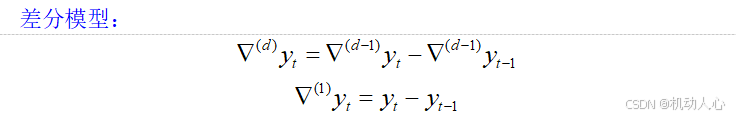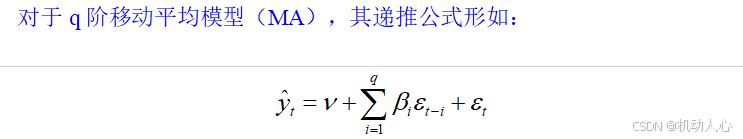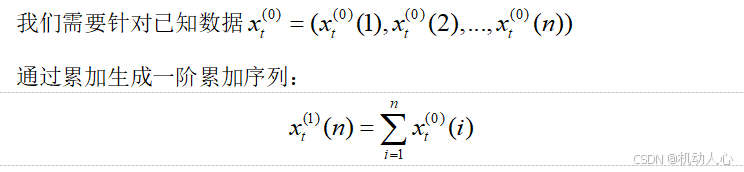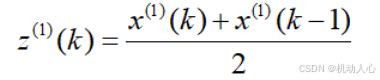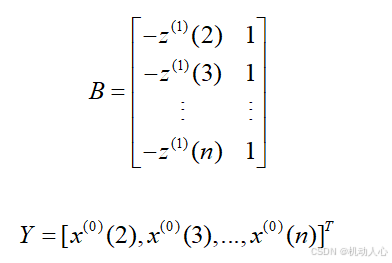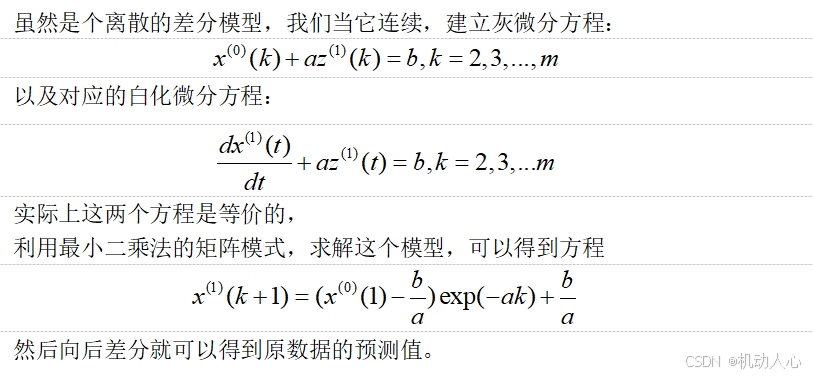Bootstrap

【数学建模导论】Task03 时间序列与投资模型

前言

按照时间排下来的序列，如果比较长的话（数据体量大），
一下子看不出什么规律，此时我们就需要用到本篇章的建模方法了。

当然预测模型可以按照以下学习路径

机器学习（多层感知机、卷积） => 时间序列（LSTM、RNN等）

❤️ ❤️ ❤️

系列文章导航

【数学建模导论】Task01 数据处理与拟合模型
【数学建模导论】Task02 权重生成与评价模型
【数学建模导论】Task03 时间序列与投资模型
【数学建模导论】Task04 机器学习
【数学建模导论】Task05 多模数据与智能模型

本篇目录导航

1 时间序列的基本概念

基本概念

顾名思义就是有时间性的序列

典型特征

数据有一个时间列作为索引
（这个时间表示的是一个先后关系）

典型应用

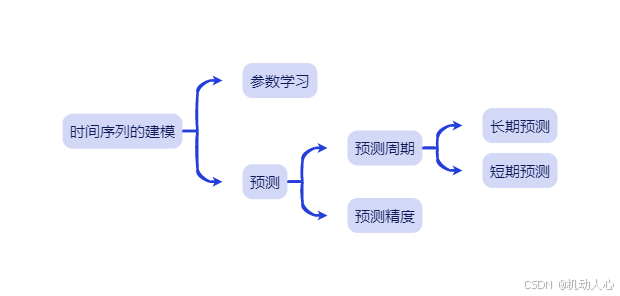
在这里插入图片描述

时间序列的建模

在这里插入图片描述

时间序列的建模

参数学习：通过模型参数分析这个序列的特征，
从而基于“领域知识”分析序列特点，挖掘出一些有意思的点子

预测：“预测周期”&“预测精度”是一对冲突概念，
如果想要精准预测那么预测周期不能够太长。

  • 对天气预报而言，我可以基于历史天气预报未来24小时内的天气情况，并且用序列建模方法可以预测得比较精准；
  • 对股票而言，我可以基于其一个月内的股价预测其接下来一周的股价变化。

时间序列的描述

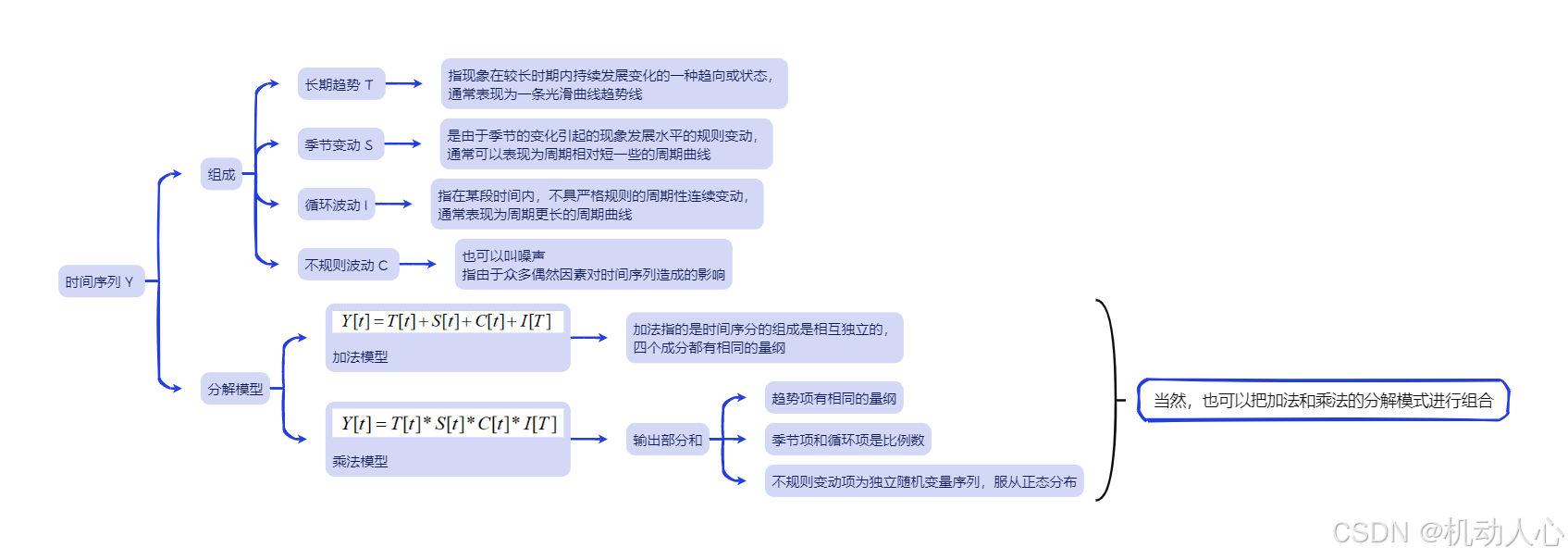
在这里插入图片描述

时间序列 Y

鼠标右键 -> 在新标签页中打开图像
在这里插入图片描述

2 移动平均法与指数平滑法

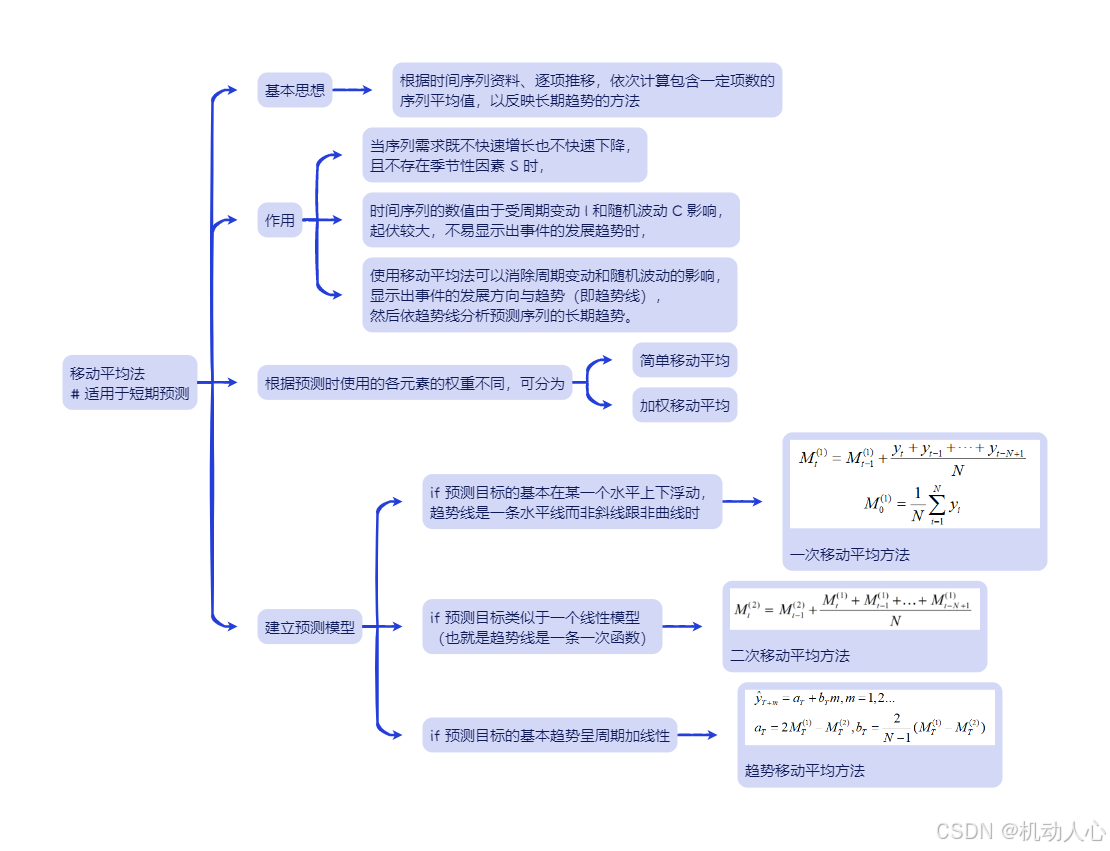
移动平均法

鼠标右键 -> 在新标签页中打开图像

在这里插入图片描述

移动平均法-建立预测模型

if 预测目标的基本趋势在某一个水平上下浮动，
趋势线是一条水平线而非斜线跟非曲线时

  • 使用一次移动平均方法
    在这里插入图片描述

if 预测目标类似于一个线性模型
（也就是趋势线是一条一次函数）

  • 使用二次移动平均方法
    在这里插入图片描述

if 预测目标的基本趋势呈周期加线性

  • 使用趋势移动平均方法
    在这里插入图片描述

N 的取值：
意味着我们计算了一个窗口长度为 N 的移动平均。
具体来说，对于每个数据点，移动平均值是该点之前（包括该点）最近的 N 个数据点的平均值。

时间序列中如果应用移动平均，
预测序列的数据量会少一个窗口长度

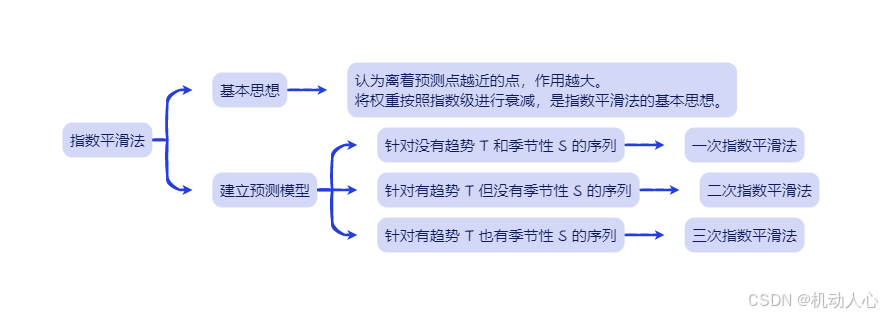
指数平滑法

鼠标右键 -> 在新标签页中打开图像

在这里插入图片描述

指数平滑法-建立预测模型

针对没有趋势 T 和季节性 S 的序列

  • 使用一次指数平滑法
    在这里插入图片描述

针对有趋势 T 但没有季节性 S 的序列

  • 使用二次指数平滑法

针对有趋势 T 也有季节性 S 的序列

  • 使用三次指数平滑法
    在这里插入图片描述

时间序列中如果应用指数平滑，
趋势线的长度和原始序列的长度是对齐的

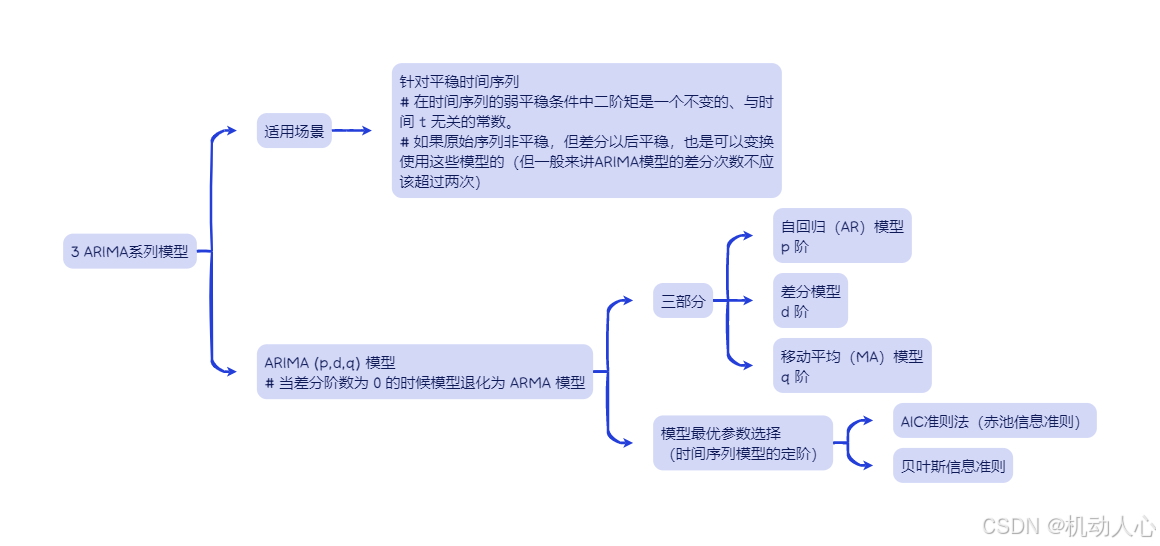
3 ARIMA系列模型

鼠标右键 -> 在新标签页中打开图像
在这里插入图片描述

ARIMA (p,d,q) 模型 - 三部分

自回归（AR）模型
- 使用**一次指数平滑法**
差分模型
在这里插入图片描述
移动平均（MA）模型
在这里插入图片描述

模型最优参数选择
（时间序列模型的定阶）

AIC准则（赤池信息准则）
在这里插入图片描述
贝叶斯信息准则
在这里插入图片描述

在这里插入图片描述

4 GARCH系列模型

鼠标右键 -> 在新标签页中打开图像
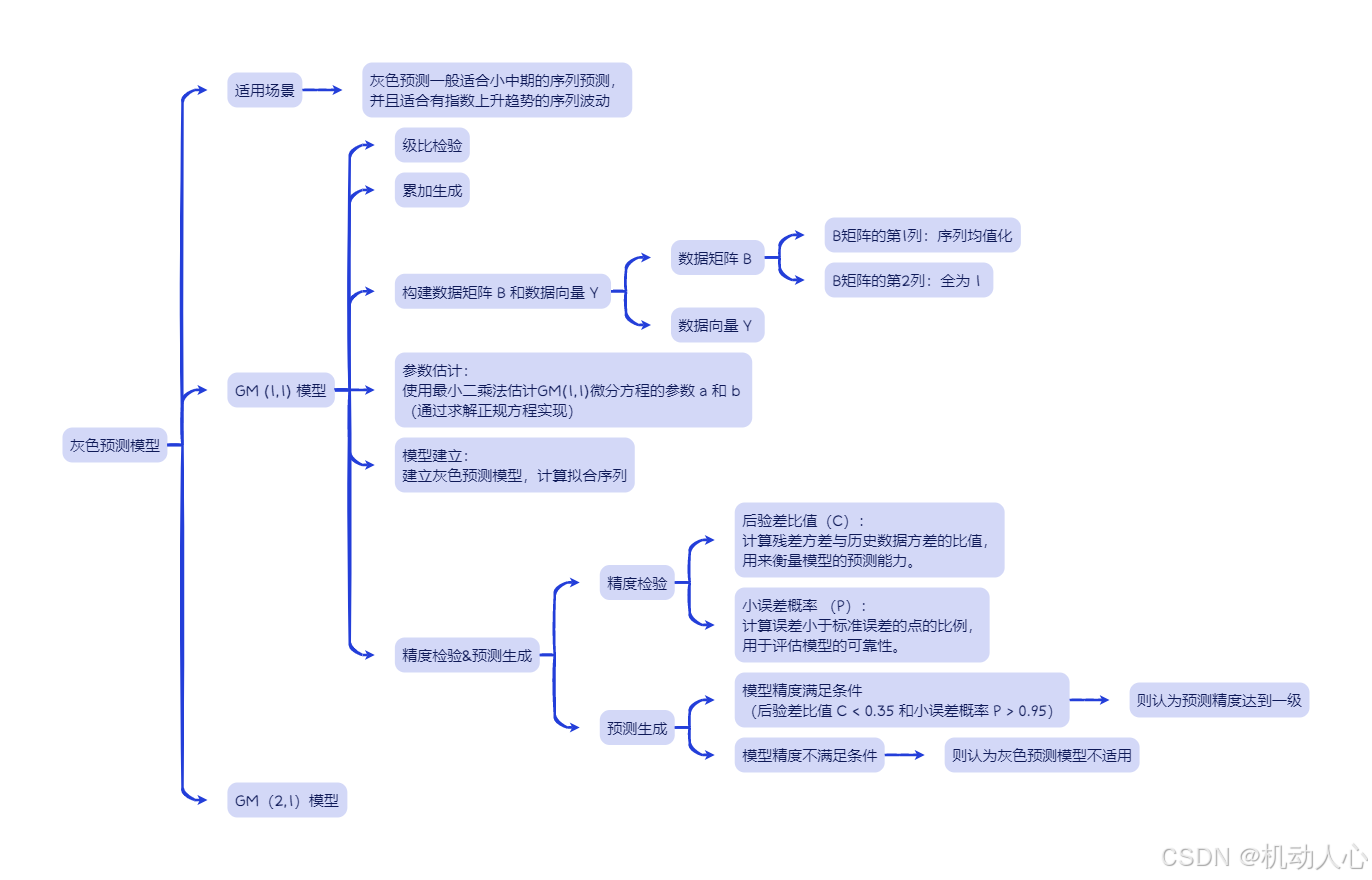
在这里插入图片描述

ARCH (P) 模型

在这里插入图片描述

GARCH (p,q) 模型

在这里插入图片描述

5 灰色系统模型

灰色预测模型

鼠标右键 -> 在新标签页中打开图像
在这里插入图片描述

GM (1,1) 模型

级比检验
在这里插入图片描述

累加生成
在这里插入图片描述

构建数据矩阵 B 和数据向量 Y
在这里插入图片描述
在这里插入图片描述

参数估计
使用最小二乘法估计GM(1,1)微分方程的参数 a 和 b
（通过求解正规方程实现）

模型建立
建立灰色预测模型，计算拟合序列
在这里插入图片描述
精度检验

  • 后验差比值（C）：
    计算残差方差与历史数据方差的比值，
    用来衡量模型的预测能力。
  • 小误差概率 （P）：
    计算误差小于标准误差的点的比例，
    用于评估模型的可靠性。

预测生成

  • if 模型精度满足条件
    （后验差比值 C < 0.35 和小误差概率 P > 0.95），
    则认为预测精度达到一级
  • if 模型精度不满足条件
    则认为灰色预测模型不适用

Python 案例代码

代码

import numpy as np
import math
import matplotlib.pyplot as plt 
%matplotlib inline
plt.rcParams['font.sans-serif']=['SimHei','Songti SC','STFangsong']      # 用来正常显示中文
plt.rcParams['axes.unicode_minus'] = False                              # 用来正常显示负号
plt.style.use("ggplot")   #风格使用ggplot


history_data = [724.57,746.62,778.27,800.8,827.75,871.1,912.37,954.28,995.01,1037.2]

# 定义 GM(1,1) 预测函数
def GM11(history_data,forcast_steps):
    n = len(history_data)       # 确定历史数据体量
    X0 = np.array(history_data) # 向量化（将历史数据转换成numpy数组）
    
    # 级比检验，检查级比是否在合理范围内，确保数据适合使用GM(1,1)模型
    lambda0=np.zeros(n-1)
    for i in range(n-1):
        if history_data[i]:
            lambda0[i]=history_data[i+1]/history_data[i]
        if lambda0[i]<np.exp(-2/(n+1)) or lambda0[i]>np.exp(2/n+2):
            print("GM11模型失效")
            return -1
    
    # 累加生成，将原数据序列转换成累加序列
    history_data_agg = [sum(history_data[0:i+1]) for i in range(n)]
    X1 = np.array(history_data_agg)
    
    # 构造 数据矩阵B和数据向量Y
    B = np.zeros([n-1,2])
    Y = np.zeros([n-1,1])
    for i in range(0,n-1):
        B[i][0] = -0.5*(X1[i] + X1[i+1])               # B矩阵的第1列：序列均值化
        B[i][1] = 1                                    # B矩阵的第2列：全为1
        Y[i][0] = X0[i+1]                              # Y向量由原数据序列的后n-1项构成
    
    # 参数估计：求解最小二乘法得到GM(1,1)微分方程的参数a和b
    A = np.linalg.inv(B.T.dot(B)).dot(B.T).dot(Y)      # 计算参数向量A
    a = A[0][0]                                        # 得到参数a
    b = A[1][0]                                        # 得到参数b
    
    # 建立灰色预测模型，计算拟合序列XX0
    XX0 = np.zeros(n)
    XX0[0] = X0[0]
    for i in range(1,n):
        XX0[i] = (X0[0] - b/a)*(1-math.exp(a))*math.exp(-a*(i))      # 计算拟合序列
    
    # 后验差比值 (C)
    e=sum(X0-XX0)/n
    aver=sum(X0)/n                  #求历史数据平均值
    s12=sum((X0-aver)**2)/n         #求历史数据方差
    s22=sum(((X0-XX0)-e)**2)/n      #求残差方差
    C = s22 / s12
    
    # 小误差概率 (P)
    cobt = 0
    for i in range(0,n):
        if abs((X0[i] - XX0[i]) - e) < 0.6754*math.sqrt(s12):       # 判断误差是否小于标准误差
            cobt = cobt+1                                           # 计数小误差数量
        else:
            cobt = cobt
    P = cobt / n                                                    # 计算小误差概率
    
    # 精度检验&预测生成
    f = np.zeros(forcast_steps)
    if (C < 0.35 and P > 0.95):                                     # 如果模型精度满足条件
        #预测精度为一级
        print('往后各年预测值为：')
        for i in range(0,forcast_steps):
            f[i] = (X0[0] - b/a)*(1-math.exp(a))*math.exp(-a*(i+n)) # 计算未来预测值
        print(f)
    else:
        print('灰色预测法不适用')
    return f


# 执行预测，预测未来20年的数据
f=GM11(history_data,20)
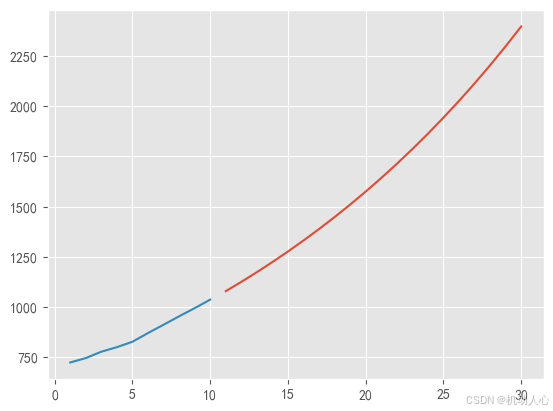
# 绘制预测结果和历史数据
plt.plot(range(11,31),f)                                            # 绘制预测数据
plt.plot(range(1,11),history_data)                                  # 绘制历史数据
plt.show()

回显

往后各年预测值为：
[1079.38044724 1125.65457636 1173.91252409 1224.23933874 1276.72371473
 1331.45814889 1388.53910348 1448.0671762  1510.14727748 1574.88881535
 1642.40588828 1712.81748628 1786.24770054 1862.8259422  1942.68717036
 2025.97212997 2112.82759985 2203.40665138 2297.86891827 2396.38087787]

在这里插入图片描述

Read more

悦读

道可道，非常道；名可名，非常名。 无名，天地之始，有名，万物之母。 故常无欲，以观其妙，常有欲，以观其徼。 此两者，同出而异名，同谓之玄，玄之又玄，众妙之门。

最新收录
gin-admin（v8）结合gin-admin-react以及gin-admin-cli踩坑记
Python numpy 平方、乘方和平方根函数
C++多态之虚表虚指针
quill编辑器自定义音频、视频、行内style样式(字符边框、首行缩进)
第19篇：python高级编程进阶：使用Flask进行Web开发
（免费送源码）计算机毕业设计原创定制：Java+ssm+MySQL 心理治愈平台
Android 布局color颜色值大全
Python+Mysql+bootstrap实现简单的web登录页面课设大作业（附源码）
谈谈对Web应用防火墙（WAF）的理解&如何处理Web应用中的敏感数据
centos杂记
;