一、公式
y
t
=
(
1
−
α
)
y
t
−
1
+
α
x
t
y_{t} = (1-\alpha) y_{t-1} + \alpha x _{t}
yt=(1−α)yt−1+αxt
其中,
x
x
x 是实际观测值
二、DataFrame.ewm() 参数
alpha、span、com、halflife 这四个参数必须选一指定
DataFrame.ewm(
com = None,
span = None,
halflife = None,
alpha = None,
min_periods = 0,
adjust = True,
ignore_na = False,
axis = 0,
times = None,
method = 'single'
)
com
- float,可选
- 根据
质心指定衰减 - α = 1 1 + c o m , c o m ≥ 0 \alpha = \frac{1}{1+com}, com≥0 α=1+com1,com≥0
span
- float,可选
- 根据
范围指定衰减 - α = 2 s p a n + 1 , s p a n ≥ 1 α=\frac{2}{span+1},span≥1 α=span+12,span≥1
halflife
- float,可选
- 根据
半衰期指定衰减 - α = 1 − e l o g 1 2 h a l l i f e , , h a l f l i f e > 0 α=1−e^{\frac{log\frac{1}{2}}{hallife},} ,halflife>0 α=1−ehallifelog21,,halflife>0
alpha
- float,可选
- 指定平滑系数α
- 0 < α ≤ 1 0<α≤1 0<α≤1
min_periods
- int,默认为0
- 窗口中具有值的最小观察数(否则结果为NA)
adjust
- bool,默认为True,即进行误差修正
- True: y t = x t + ( 1 − α ) x t − 1 + ( 1 − α 2 ) x t − 2 + . . . + ( 1 − α t ) x 0 1 + ( 1 − α ) + ( 1 − α 2 ) + . . . + ( 1 − α t ) y_{t} = \frac{x_{t}+(1-\alpha)x_{t-1}+(1-\alpha ^{2})x_{t-2}+...+(1-\alpha ^{t})x_{0}}{1+(1-\alpha)+(1-\alpha ^{2})+...+(1-\alpha ^{t})} yt=1+(1−α)+(1−α2)+...+(1−αt)xt+(1−α)xt−1+(1−α2)xt−2+...+(1−αt)x0
- Fasle:
y 0 = x 0 , t = 0 y t = ( 1 − α ) y t − 1 + α x t , t > 0 \begin{aligned} & y_{0} = x_{0} , & t = 0 \\ & y_{t} = (1-\alpha) y_{t-1} + \alpha x _{t}, & t>0 \end{aligned} y0=x0,yt=(1−α)yt−1+αxt,t=0t>0
ignore_na
-
bool,默认为False
-
计算权重时忽略缺失值;指定True重现0.15.0版本之前的行为。
axis
- {0或者’index’,1或‘columns’},默认为0,标识行,值1标识列。
三、python 案例
- 生成测试数据集
import pandas as pd
data = [203.8,214.1,229.9,223.7,220.7,198.4,207.8,228.5,206.5,226.8,247.8,259.5]
df = pd.DataFrame(data,columns=['data'])
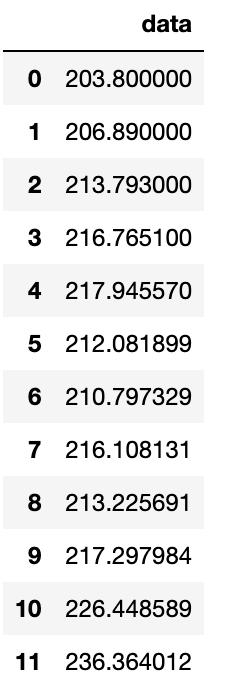
- 使用ewm函数计算指数加权移动平均
- α = 0.3 \alpha=0.3 α=0.3
- 不进行误差修正,即采用 y t = ( 1 − α ) y t − 1 + α x t , t > 0 y_{t} = (1-\alpha) y_{t-1} + \alpha x _{t}, t>0 yt=(1−α)yt−1+αxt,t>0
- y 1 = 0.7 ∗ 203.8 + 0.3 ∗ 214.1 = 206.89 y_{1} = 0.7*203.8+0.3*214.1 = 206.89 y1=0.7∗203.8+0.3∗214.1=206.89
df.ewm(alpha=0.3,adjust=False).mean()