逻辑回归算法
逻辑回归算法
逻辑回归(Logistic Regression)是一种广泛使用的统计方法和机器学习算法,主要用于解决二分类问题。尽管名字中包含“回归”,但它实际上是一种分类技术,用于预测一个事件发生的概率,即输出结果属于某一类别的概率。
已有数据:
| 名称 | 体温 | 胎生 | 水生 | 飞行 | 有腿 | 是否为哺乳类? |
|---|---|---|---|---|---|---|
| 青蛙 | 冷血 | 否 | 半 | 否 | 是 | 否(0) |
| 鸽子 | 恒温 | 否 | 否 | 是 | 是 | 否(0) |
| 猪 | 恒温 | 是 | 否 | 否 | 是 | 是(1) |
| 蝙蝠 | 恒温 | 是 | 否 | 是 | 是 | 是(1) |
| 鲸鱼 | 恒温 | 是 | 是 | 否 | 否 | 是(1) |
预测分类:
| 名称 | 体温 | 胎生 | 水生 | 飞行 | 有腿 | 是否为哺乳类? |
|---|---|---|---|---|---|---|
| 猫 | 恒温 | 是 | 否 | 否 | 是 | ? |
1.算法步骤
-
数据预处理
- 目标:准备适合模型训练的数据格式;
- 关键步骤:
- 特征标准化:将特征缩放到均值为0、方差为1(如
zscore函数); - 添加偏置项:在特征矩阵中添加一列全 1(对应截距项);
- 标签编码:二分类标签映射为0和1。
- 特征标准化:将特征缩放到均值为0、方差为1(如
-
定义假设函数(Sigmoid 函数)
- 逻辑回归通过 Sigmoid 函数将线性回归结果映射到概率值: h θ ( x ) = 1 1 + e − θ T x h_θ(x)=\frac{1}{1+e^{-θ^T\mathbf{x}}} hθ(x)=1+e−θTx1其中: θ θ θ 为模型参数(权重向量), x \mathbf{x} x 为输入特征向量。
-
构建损失函数(交叉熵损失)
- 损失函数衡量预测值与真实值的差异: J ( θ ) = − 1 m ∑ i = 1 m [ y ( i ) log ( h θ ( x ( i ) ) ) + ( 1 − y ( i ) ) log ( 1 − h θ ( x ( i ) ) ) ] J(θ)=-\frac{1}{m} \sum_{i=1}^{m}[y^{(i)}\log(h_θ(x^{(i)}))+(1-y^{(i)})\log(1-h_θ(x^{(i)}))] J(θ)=−m1i=1∑m[y(i)log(hθ(x(i)))+(1−y(i))log(1−hθ(x(i)))]其中 m m m 为样本数量, y ( i ) y^{(i)} y(i) 为第 i i i 个样本的真实标签(0或1)。
-
参数优化(梯度下降)
- 通过迭代更新参数
θ
θ
θ,最小化损失函数:
θ
j
:
=
θ
j
−
α
∂
J
(
θ
)
∂
θ
j
θ_j:=θ_j−α\frac{∂J(θ)}{∂θ_j}
θj:=θj−α∂θj∂J(θ)其中
α
α
α 为学习率,这里的
:=是一个赋值操作,意味着将右边计算的结果赋值给左边的变量。这是说根据损失函数 J ( θ ) J(θ) J(θ) 关于 θ j θ_j θj 的偏导数调整参数 θ j θ_j θj 的值。 - 梯度计算公式: ∂ J ( θ ) ∂ θ j = 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) \frac{∂J(θ)}{∂θ_j}=\frac{1}{m} \sum_{i=1}^{m} (h_θ(x^{(i)})-y^{(i)})x_j^{(i)} ∂θj∂J(θ)=m1i=1∑m(hθ(x(i))−y(i))xj(i)
- 通过迭代更新参数
θ
θ
θ,最小化损失函数:
θ
j
:
=
θ
j
−
α
∂
J
(
θ
)
∂
θ
j
θ_j:=θ_j−α\frac{∂J(θ)}{∂θ_j}
θj:=θj−α∂θj∂J(θ)其中
α
α
α 为学习率,这里的
-
模型预测
- 将概率值转换为类别标签: 预测类别 = { 1 , h θ ( x ) ≥ 0.5 0 , h θ ( x ) < 0.5 预测类别=\begin{cases}1,\quad h_θ(x)\geq 0.5\\0, \quad h_θ(x)<0.5 \end{cases} 预测类别={1,hθ(x)≥0.50,hθ(x)<0.5
-
评估指标
- 回归显著性:
- 整个回归模型的显著性:要求整个模型的 p − v a l u e / S i g . < 0.05 p-value/Sig.<0.05 p−value/Sig.<0.05 ;
- 拟合优度的显著性:要求 Hosmer-Lemeshow 检验的 p − v a l u e / S i g . > 0.05 p-value/Sig.>0.05 p−value/Sig.>0.05 。
- 模型拟合优度:
- 伪
R
2
R^2
R2
- Cox & Snel R 2 R^2 R2 ,要求在0.3以上;
- Nagelkerke R 2 R^2 R2,要求在0.4以上;
- R 2 R^2 R2 的要求会有学科的差别,请注意。
- 对数似然值(Log-likelihood)越大越好;
- AIC 赤池信息准则或 BIC 贝叶斯信息准则越小越好;
- 伪
R
2
R^2
R2
- 混淆矩阵:
- TP:预测为正,实际确实也为正;
- TF:预测为负,实际确实也为负;
- TN:预测为正,但实际不是正的;
- FN:预测为负,但实际不是负的;
- 准确率: O v e r a l l p e r c e n t a g e = T P + T F T P + T N + F P + F N Overall percentage =\frac{TP + TF }{ TP + TN + FP + FN } Overallpercentage=TP+TN+FP+FNTP+TF;
- 精确率 = T P T P + F P 精确率 =\frac{TP}{TP+FP} 精确率=TP+FPTP ,强调误报的影响;
- 召回率 = T P T P + F N 召回率 =\frac{TP}{TP+FN} 召回率=TP+FNTP ,强调漏报的影响。
- ROC曲线与AUC值:评估分类器整体性能。
- ROC 曲线是描述不同假阳率(FPR)和真阳率(TPR)之间关系的工具;
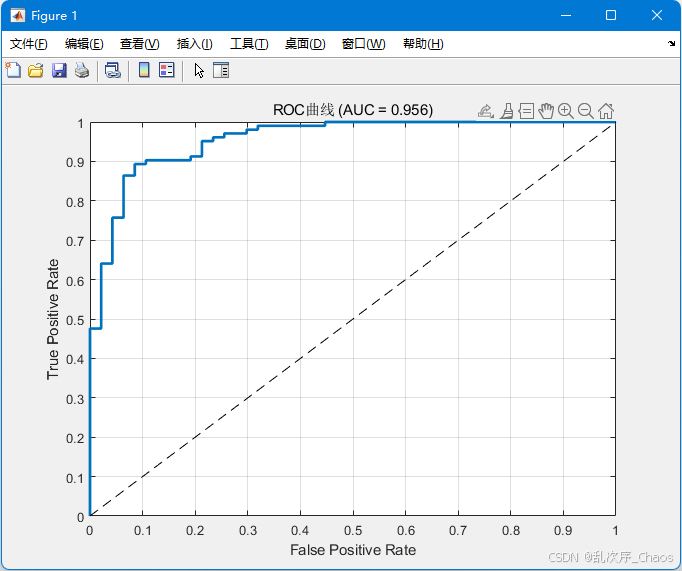
- 重点看 AUC ,AUC 要求大于0.5,否则逻辑回归的效果等于甚至小于随机概率。
- 回归显著性:
2. MATLAB 实现
预测用户是否会购买商品(二分类问题),基于以下特征:
visit_freq: 用户每周访问次数;cart_add: 加入购物车次数;coupon_used: 是否使用优惠券(0/1);purchased: 是否购买(目标变量,0/1)。
真实公式为:
p
u
r
c
h
a
s
e
d
=
1
1
+
e
0.5
+
1.2
∗
v
i
s
i
t
f
r
e
q
−
0.8
∗
c
a
r
t
a
d
d
+
2.0
∗
c
o
u
p
o
n
u
s
e
d
purchased=\frac{1}{1+e^{0.5+1.2*visit_{freq}-0.8*cart_{add}+2.0*coupon_{used}}}
purchased=1+e0.5+1.2∗visitfreq−0.8∗cartadd+2.0∗couponused1
训练所得模型为:
p
u
r
c
h
a
s
e
d
=
1
1
+
e
0.1108
+
3.7808
∗
v
i
s
i
t
f
r
e
q
−
1.6010
∗
c
a
r
t
a
d
d
+
2.2980
∗
c
o
u
p
o
n
u
s
e
d
purchased=\frac{1}{1+e^{0.1108+3.7808*visit_{freq}-1.6010*cart_{add}+2.2980*coupon_{used}}}
purchased=1+e0.1108+3.7808∗visitfreq−1.6010∗cartadd+2.2980∗couponused1
%% 电商逻辑回归案例(含完整评价指标)
% 功能: 预测用户购买行为
clc; clear; close all;
%% 1. 生成模拟电商数据
rng(0); % 固定随机种子
m = 500; % 样本数量
% 生成特征数据
visit_freq = 2 + 3*randn(m,1); % 正态分布模拟访问频率
cart_add = poissrnd(3, m,1); % 泊松分布模拟购物车添加次数
coupon_used = randi([0,1], m,1); % 是否使用优惠券(0/1)
% 生成目标变量(购买概率)
beta_true = [0.5, 1.2, -0.8, 2.0]; % 真实参数 [截距, visit_freq, cart_add, coupon_used]
X = [ones(m,1), visit_freq, cart_add, coupon_used];
prob = 1 ./ (1 + exp(-X * beta_true')); % Logistic函数
purchased = binornd(1, prob); % 生成二分类目标变量
% 合并数据表
data = table(visit_freq, cart_add, coupon_used, purchased, ...
'VariableNames', {'visit_freq', 'cart_add', 'coupon_used', 'purchased'});
%% 2. 数据预处理
% 标准化连续变量(可选,但对收敛有帮助)
data.visit_freq = zscore(data.visit_freq);
data.cart_add = zscore(data.cart_add);
% 划分训练集和测试集(70%训练,30%测试)
cv = cvpartition(m, 'HoldOut', 0.3);
trainData = data(cv.training,:);
testData = data(cv.test,:);
%% 3. 训练逻辑回归模型
model = fitglm(trainData, 'purchased ~ visit_freq + cart_add + coupon_used', ...
'Distribution', 'binomial');
model_null = fitglm(trainData, 'purchased ~ 1', 'Distribution', 'binomial','Link', 'logit');
% 显示模型摘要(包含系数p值)
disp('模型系数及显著性:');
disp(model.Coefficients);
%% 4. 回归显著性检验
% 整个模型显著性(似然比检验)
model_pvalue = model.coefTest; % 模型p-value
fprintf('\n模型显著性 p-value = %.4f (需 <0.05)\n', model_pvalue);
% Hosmer-Lemeshow拟合优度检验(需自定义函数)
[HL, HL_pvalue] = hosmerLemeshowTest(model.Fitted.Probability, trainData.purchased, 10);
fprintf('Hosmer-Lemeshow检验 p-value = %.4f (需 >0.05)\n', HL_pvalue);
%% 5. 模型拟合优度指标
% 伪R²计算
logLikelihood_null = model_null.LogLikelihood; % 零模型对数似然
logLikelihood_full = model.LogLikelihood; % 完整模型对数似然
% Cox & Snell R²
cox_snell_R2 = 1 - exp(-2/m * (logLikelihood_full - logLikelihood_null));
% Nagelkerke R²
nagelkerke_R2 = (1 - exp(-2/m * (logLikelihood_full - logLikelihood_null))) / (1 - exp(2/m * logLikelihood_null));
fprintf('\nCox & Snell R² = %.3f (需 >0.3)\n', cox_snell_R2);
fprintf('Nagelkerke R² = %.3f (需 >0.4)\n', nagelkerke_R2);
% 信息准则
AIC = model.ModelCriterion.AIC;
BIC = model.ModelCriterion.BIC;
fprintf('AIC = %.2f, BIC = %.2f (越小越好)\n', AIC, BIC);
%% 6. 混淆矩阵与分类指标
% 预测测试集概率
testProb = predict(model, testData);
testPred = testProb > 0.5; % 阈值0.5
% 计算混淆矩阵
confMat = confusionmat(double(testData.purchased), double(testPred));
TP = confMat(2,2);
TN = confMat(1,1);
FP = confMat(1,2);
FN = confMat(2,1);
% 分类指标
accuracy = (TP + TN) / sum(confMat(:));
precision = TP / (TP + FP);
recall = TP / (TP + FN);
fprintf('\n混淆矩阵:\n');
disp(confMat);
fprintf('准确率 = %.2f%%, 精确率 = %.2f%%, 召回率 = %.2f%%\n', ...
accuracy*100, precision*100, recall*100);
%% 7. ROC曲线与AUC值
[X_roc, Y_roc, ~, AUC] = perfcurve(testData.purchased, testProb, 1);
figure;
plot(X_roc, Y_roc, 'LineWidth', 2);
hold on;
plot([0 1], [0 1], 'k--');
xlabel('False Positive Rate');
ylabel('True Positive Rate');
title(sprintf('ROC曲线 (AUC = %.3f)', AUC));
grid on;
参考资料
[1] 20分钟用人话教会你逻辑回归是什么-哔哩哔哩
[2] 【机器学习】逻辑回归十分钟学会,通俗易懂(内含spark求解过程)-哔哩哔哩
[3] 【五分钟机器学习】机器分类的基石:逻辑回归Logistic Regression-哔哩哔哩