基于禁忌搜索算法的TSP问题最优路径搜索matlab仿真

1.程序功能描述

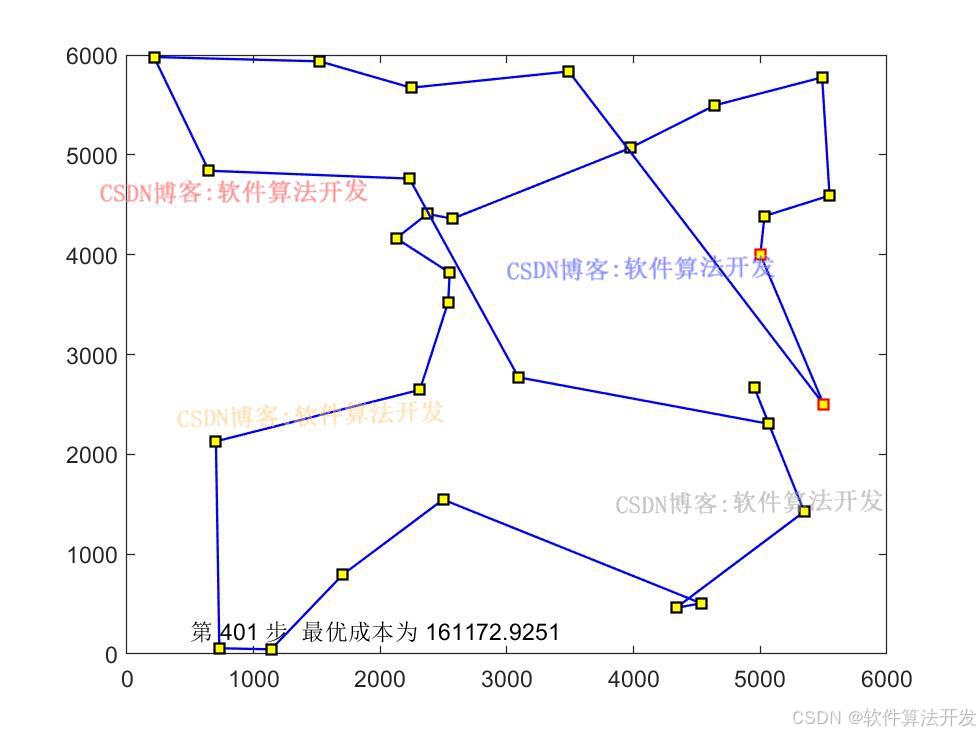
基于禁忌搜索算法的TSP问题最优路径搜索，旅行商问题（TSP）是一个经典的组合优化问题。其起源可以追溯到 19 世纪初，最初是在物流配送、线路规划等实际场景中被提出。简单来说，给定一组城市和城市之间的距离，旅行商需要从一个城市出发，访问每个城市恰好一次，最后回到起始城市，目标是找到总路程最短的路线。

2.测试软件版本以及运行结果展示

MATLAB2022A版本运行

3.核心程序

..........................................................................
% 定义城市的数量为 30
Ncity = 30; 
% 定义装卸速度为 0.8
v1    = 0.8; %装卸速度
% 定义行车速度为 20
v2    = 20; %行车速度
% 定义固定损耗成本为 20
c     = 20; %固定损耗成本
% 定义车损与载重质量的损耗系数为 0.025
r     = 0.025; %车损与载重质量的损耗系数
% 生成装货时间数组，第一个和最后一个元素为 0，中间元素为随机数
q     = [0,10*rand(1,Ncity-2),0]; %装货时间
% 生成等待时间数组，第一个元素为 0，其余元素为随机数
t1    = [0,20*rand(1,Ncity-1)]; %等待时间
% 生成最晚时间窗数组，元素为随机数
t2    = [50*rand(1,Ncity-1)]; %最晚时间窗
% 生成城市坐标矩阵，第一个和最后一个坐标为特定值，中间元素为随机数
Clist = [[5000,4000];6000*rand(Ncity-2,2);[5500,2500]]; 
% 初始化距离矩阵 Mlist
for i=1:Ncity
    for j=1:Ncity
        % 计算城市 i 和城市 j 之间的欧几里得距离，并存储在 Mlist 中
        Mlist(i,j) = sqrt((Clist(i,1)-Clist(j,1))^2 + (Clist(i,2)-Clist(j,2))^2); 
    end
end

...............................................................................
% 创建新的图形窗口
figure; 
% 用红色绘制最优成本的变化曲线，线宽为 2
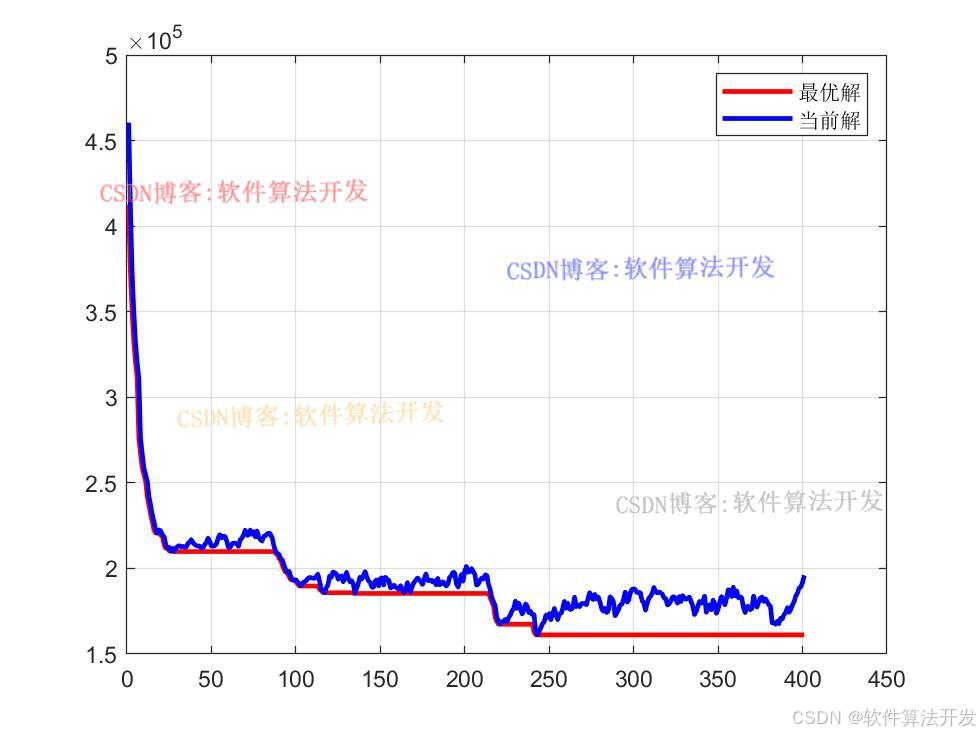
plot(yfitsave,'r','LineWidth',2); 
hold on; 
% 用蓝色绘制当前解的适应度变化曲线，线宽为 2
plot(tmps2,'b','LineWidth',2); 
% 显示网格
grid; 
% 显示图例，区分最优解和当前解
legend('最优解','当前解'); 
90

4.本算法原理

禁忌搜索（Tabu Search，TS）算法是一种元启发式算法，它最早由 Fred Glover 在 1986 年提出。它的灵感来源于人们在解决复杂问题时的记忆和避免重复错误的行为。最初用于解决整数规划问题，后来被广泛应用于各种组合优化问题，包括 TSP。随着研究的深入，学者们对禁忌搜索算法进行了诸多改进，如改进禁忌列表的结构、动态调整禁忌长度等，以提高算法的性能。

禁忌列表（Tabu List）

禁忌列表是禁忌搜索算法的核心概念之一。它是一个存储结构，用于记录最近访问过的解或移动操作，以避免算法在短时间内重复访问这些解或执行相同的操作。通过禁止算法在一定步数内再次访问禁忌列表中的元素，使得搜索过程能够跳出局部最优解，增加搜索的多样性。例如，在 TSP 中，如果刚刚交换了城市和城市的访问顺序，那么在禁忌列表规定的禁忌期内，禁止再次交换这两个城市的顺序。

假设禁忌列表是一个先进先出（FIFO）的队列。当执行一个移动操作（如交换两个城市的访问顺序）时，将这个操作记录在禁忌列表的头部。在每次选择新的移动操作时，检查该操作是否在禁忌列表中。如果在禁忌列表中，根据藐视准则（后面会介绍）来决定是否仍然执行这个操作。

禁忌长度（Tabu Tenure）

禁忌长度是指一个解或移动操作在禁忌列表中被禁止访问或执行的步数。它是一个重要的参数，直接影响算法的搜索能力。对搜索能力的影响：如果禁忌长度太短，算法可能会很快重新访问之前的解，陷入局部最优解；如果禁忌长度太长，可能会过度限制搜索空间，导致算法搜索效率低下，错过一些潜在的好解。例如，在 TSP 中，如果禁忌长度设置为 1，那么可能刚刚禁止交换两个城市的顺序，下一次就又可以交换了，这样很难跳出局部最优；而如果禁忌长度设置为（为城市数量，这是所有可能的城市交换操作的数量），那么算法可能会在很长时间内无法访问一些可能的好解。

确定合适的禁忌长度可以通过实验和经验来选择。一种常见的方法是根据问题的规模和性质，设置禁忌长度为一个与问题规模相关的函数。例如，在 TSP 中，可以设置禁忌长度为（为城市数量），并在算法运行过程中根据搜索情况动态调整。

藐视准则（Aspiration Criterion）

藐视准则是一种机制，用于在某些情况下允许算法访问禁忌列表中的解。当一个禁忌解满足一定的条件时，算法可以选择这个解，即使它在禁忌列表中。

它可以避免算法因为过度禁忌而错过一些可能是全局最优的解。例如，在 TSP 中，如果一个被禁忌的城市交换操作能够产生一个比当前找到的最优解还要好的解，那么根据藐视准则，算法可以执行这个操作。

5.完整程序

VVV