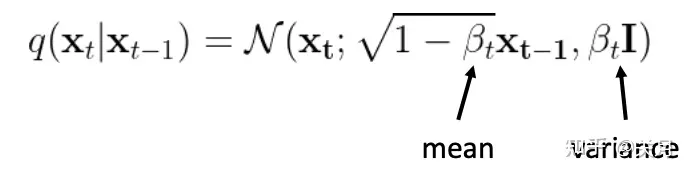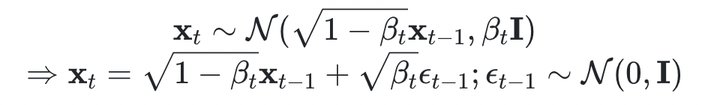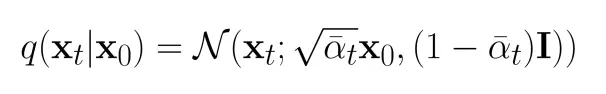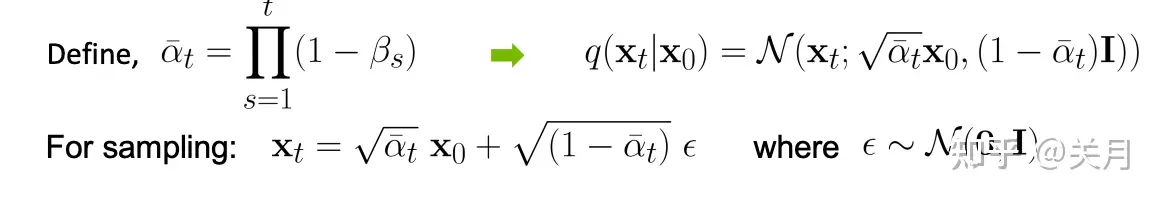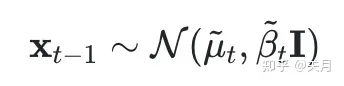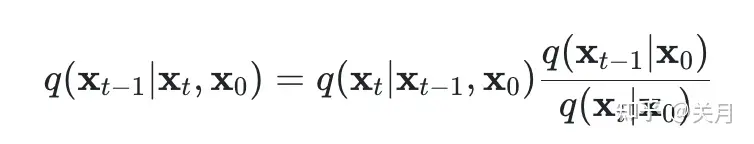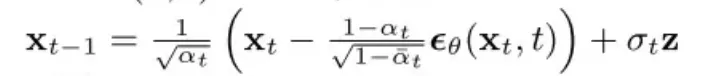论文:Denoising Diffusion Probabilistic Models
概述
扩散模型可以简单的概括为加噪和去噪两个过程:
加噪:使图像 �0 最终变成了一个标准的正态分布 �� 。
去噪:将 ��还原为 �0 。
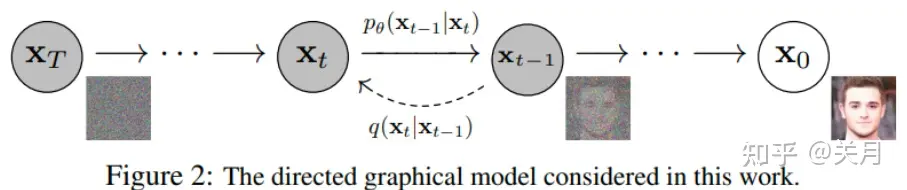
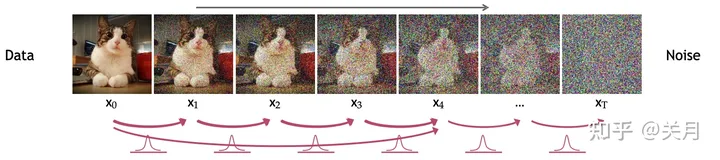
实质上扩散模型需要学习的是去噪的过程,而加噪的过程为去噪过程的训练提供了训练的标签, 如下图所示,从右到左就是一个加噪的过程,从左到右就是一个去噪的过程。
加噪
那么怎么加噪呢?DDPM是这样设计的,构建一个与 ��−1 相关的正态分布,让x_t从这个正态分布中采样就可以了:
��∼�(��(��−1),��2�)
那么 ��(��−1),��2 (分别是正态分布的均值和方差)具体是怎么设置的呢?
��∼�(1−����−1,���)
换成概率的形式写(�� 是从 10−4 到 10−2 线性增长的值)就是:
mean是均值,variance是方差
为什么要这样设置呢?先给出一个结论,这样设置正态分布的均值和方差能让 �0 由慢到快的变成一个均值为0,方差为I的正态分布(也就是概述里说的加噪的目标), 下面再继续推理一下,根据参数重整化技巧(下面会说说),可以写成下面的形式:
一看这个式子就可以递推(这里就不推了),最终可以得到 �0 生成任意时刻 �� 的一个公式:
��=�¯��0+1−�¯��
同样写成概率分布的形式(其中 ��=1−�� , �¯�=∏�=1��� ):
再来看上面给出的结论, 就可以根据这个公式来理解了,这个公式里的 �� 是一个小于1的常数。在DDPM论文中,�� 从 �1=10−4 到 ��=10−2 线性增长。这样, �� 变大, �� 也越小, �¯� 趋近于0的速度越来越快,最后 �� 几乎为0,代入上面的 ��=�¯��0+1−�¯�� 中, �� 就满足标准正态分布了,符合我们对扩散模型的要求,即这个加噪声公式能够从慢到快的改变原图像,让图像最终均值为0,方差为I。 �� 在别的文章里也可以称为扩散率,是一个给定的比较小的值,大于0小于1,随扩散步骤增大而增大。
那么什么是参数重整化呢:如果希望从高斯分布 �(�,�2) 中采样,可以从标准正态分布 �(0,1) 中采样出 � , 再通过 �∗�+� 得到的就等价于高斯分布 �(�,�2) 中采样。为什么要这样参数重整化呢? 不是很明白,感觉是为了引入这个噪声z,其它部分的就都成了定量了。
上面这个就是全部的前向过程了,也就是加噪过程,整理一下,得到了下面的公式:
去噪
加噪之后怎么去噪呢?有一个数学原理(有办法证明的):当 �� 足够小时,每一步加噪声的逆操作也满足正态分布。换句话说,如果�(��−1|��) 满足高斯分布而且方差��足够小时,则 �(��|��−1) 也满足高斯分布。这个也就是说,去噪过程也可以像加噪过程一样,��−1可以从��相关的均值和方差中采样得到(加噪过程是构建了一个与 ��−1 相关的正态分布,让 �� 从这个正态分布中采样),最终得到原图 �0 , 即下面的公式(、��、�� 都是和 �� 和t相关的):
概率分布的形式
也就是说我们可以构建两个函数(也就是神经网络),以 �� 和t为输入,预测、��、�� 。但是预测是能预测,什么作为标签呢? 文章开头我们就说了加噪的过程就是为了给去噪提供标签的,那么怎么提供呢?怎么让 �(��−1|��) 和 �(��|��−1) 联系起来呢?伟大的贝叶斯定理:
根据上面的公式,就可以推出 �(��−1|��) 应该满足的正态分布的均值和方差了(很多文章都推过了,这里就略过了):
�~�=1��(��−1−��1−�¯���) �~�=1−�¯�−11−�¯�⋅��
�~� 分别就是均值和方差,我们就可以构建两个函数(也就是神经网络),以��和t为输入,预测 、��、�� ,而且标签也有了。但是再仔细分析一下上面的均值和方差:
均值:除了 �� 其他的都是定值 方差:都是定值
所以其实我们也不需要构建两个神经网络去预测均值和方差,只需要预测一个 �� 就可以了。假设这个神经网络名为 �� ,那么DDPM的损失函数可以写成:
�=||��−��(��,�)||2
至此,就是整个的训练过程了,训练好了怎么推理呢?就还是正常的去噪过程,��−1从��相关的均值和方差中采样得到,这个均值和方差我们已经通过神经网络预测出来的。
��(��,�)=1��(��−1−��1−�¯���(��,�)) ��2=1−�¯�−11−�¯�⋅��
还有一个小技巧,在方差的选择上,通过实验发现方差也可以采用和加噪声时的方差一样, ��2=�� ,两者都能产生差不多的结果。实验的时候发现当 �0 是特定的某个数据是,用上一节推导出来的方差最好。当 �0∼�(0,�) 是采用和加噪声时的方差效果比较好。采样是也是利用参数重整化的技巧,公式如下,其中的 � 方差就可以根据�0的情况选择了。
参考链接
扩散模型(Diffusion Model)详解:直观理解、数学原理、PyTorch 实现
https://www.cs.unc.edu/~ronisen/teaching/fall_2022/pdf_lectures/lecture8_diffusion_model.pdf
编辑于 2023-08-31 10:35・IP 属地